Ficha Formativa – Energia do Sol para a Terra

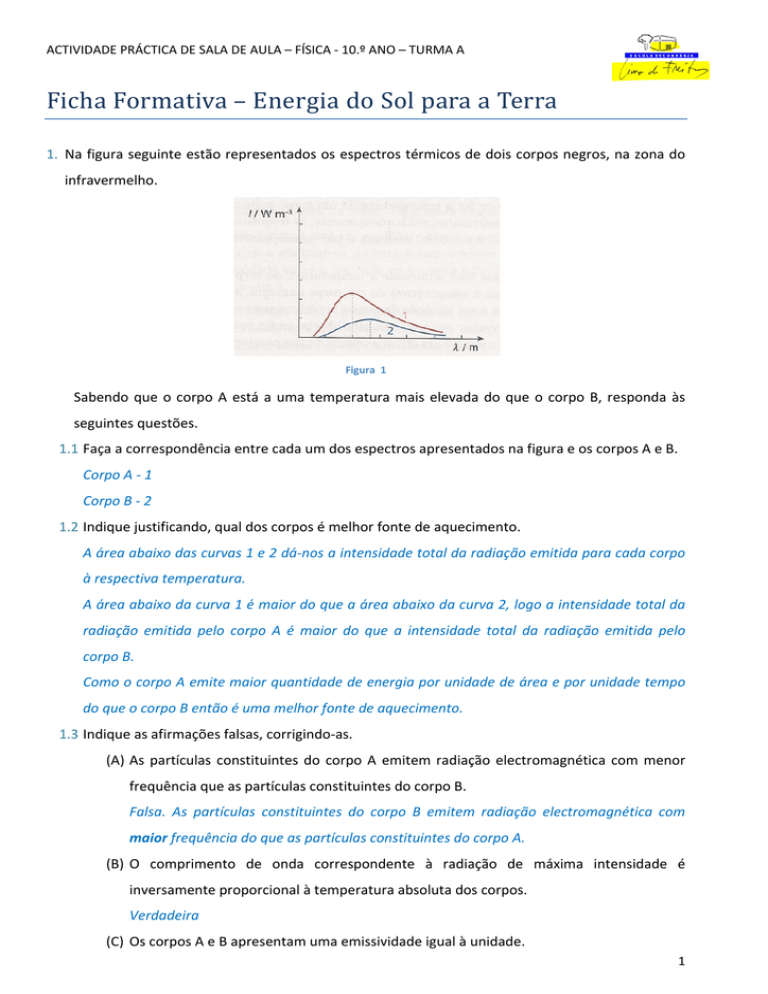
ACTIVIDADE PRÁCTICA DE SALA DE AULA – FÍSICA ‐ 10.º ANO – TURMA A Ficha Formativa – Energia do Sol para a Terra 1. Na figura seguinte estão representados os espectros térmicos de dois corpos negros, na zona do infravermelho. Figura 1 Sabendo que o corpo A está a uma temperatura mais elevada do que o corpo B, responda às seguintes questões. 1.1 Faça a correspondência entre cada um dos espectros apresentados na figura e os corpos A e B. Corpo A ‐ 1 Corpo B ‐ 2 1.2 Indique justificando, qual dos corpos é melhor fonte de aquecimento. A área abaixo das curvas 1 e 2 dá‐nos a intensidade total da radiação emitida para cada corpo à respectiva temperatura. A área abaixo da curva 1 é maior do que a área abaixo da curva 2, logo a intensidade total da radiação emitida pelo corpo A é maior do que a intensidade total da radiação emitida pelo corpo B. Como o corpo A emite maior quantidade de energia por unidade de área e por unidade tempo do que o corpo B então é uma melhor fonte de aquecimento. 1.3 Indique as afirmações falsas, corrigindo‐as. (A) As partículas constituintes do corpo A emitem radiação electromagnética com menor frequência que as partículas constituintes do corpo B. Falsa. As partículas constituintes do corpo B emitem radiação electromagnética com maior frequência do que as partículas constituintes do corpo A. (B) O comprimento de onda correspondente à radiação de máxima intensidade é inversamente proporcional à temperatura absoluta dos corpos. Verdadeira (C) Os corpos A e B apresentam uma emissividade igual à unidade. 1 Verdadeira 2.
Por se encontrarem a uma determinada temperatura, todos os corpos emitem um conjunto de radiações electromagnéticas. A radiação emitida apresenta um máximo de intensidade para um determinado comprimento de onda, máx. Completa a seguinte tabela. Temperatura máx 623 K ........... m Terra .........°C 10,1 m Resistência de um forno 250 °C ...........nm Planeta Neptuno ..........K 50,8 x 103 nm Sol 5800 K ............nm Corpo Planeta Mercúrio Tabela 1 
á
Planeta Mercúrio: 
á ,
,
Terra: 1 
10 10,1 2,898 10
1,01 10
287
1,01
10
287 273 Resistência de um forno: 
273 á 1 10 523 250 ,
5,54
,
10 ,
Planeta Neptuno: 1 10 50,8 2,898 10
5,08 10
10 5,08
10
, Sol: 2 
á ,
,
4,996 10 1 10 ,
3.
O orifício da fechadura de um armário tem a área de 1,0 cm2 e a sua temperatura é igual à do interior do armário, 22 °C. Quantos kJ estão a ser irradiados pelo orifício da fechadura, em cada segundo, sabendo que este actua como um corpo negro.  ∆
273 ∆ 1 5,67 295 0,00010 1,0 4,3 4.
22 10
10
0,00010 1
4,3 295 10
4,3 10 , O gráfico abaixo representa a radiância espectral (potência da radiação emitida por unidade de área em cada comprimento de onda) para três estrelas A, B e C a temperaturas diferentes que se comportam como um corpo negro. As temperaturas das estrelas são 3200 K, 5800 K e 7000 K. Figura 2 4.1 Identifique os valores das temperaturas das estrelas A, B e C. Estrela A ‐ 3200 K Estrela B – 5800 K Estrela C – 7000 K 4.2 Estabeleça a correspondência entre as temperaturas das estrelas e as cores de cada estrela. 3200 K Amarela 5800 K Vermelha 7000 K Azul 3 4.3 Selecciona a opção correcta. Os comprimentos de onda para os quais é máxima a radiância espectral das estrelas a 5800 K e 7000 K relacionam‐se entre si por: (A)


(B)


(C)


(D)



á á
á á
á á
á á
á
5800 
á
7000 7000
á
á
5800 á



7000 5800 5800
7000
7000
5800
5800
7000
(B) 4.4 Indique as afirmações falsas, corrigindo‐as. (A) O gráfico do espectro da radiação térmica permite obter a energia emitida pela estrela com um dado comprimento de onda. Falsa. O gráfico do espectro da radição térmica permite obter a energia por unidade de tempo e por unidade de área emitida pela estrela com um dado comprimento de onda (B) Um corpo negro é o melhor absorsor e o melhor emissor. Verdadeira (C) A intensidade da radiação emitida por uma estrela é directamente proporcional à quarta potência da temperatura absoluta superficial da estrela. Verdadeira (D) A emissividade de uma estrela é próxima de 1. Verdadeira (E) O máximo da curva do espectro da radiação térmica desloca‐se para maiores comprimentos de onda quando a temperatura aumenta. Falsa. O máximo da curva do espectro da radiação térmica desloca‐se para menores comprimentos de onda quando a temperatura aumenta 4 5. Um leitor de CD‐ROM utiliza um laser que opera a 3,84 x 1014 Hz, com uma potência média de 5 mW; um laser de díodo utilizado na tecnologia DVD opera a 650 nm, com uma potência média de 8 mW; a tecnologia Blu‐ ray Disc utiliza um laser que opera a 7,40 x 1014 Hz. 5.1 Identifique a região do espectro electromagnético em que operam cada um destes lasers. Consultar o espectro electromagnético CD‐ROM: Infravermelho DVD Visível Blu‐ ray Disc Visível 5.2 Indique se possível a cor da radiação emitida por cada um dos lasers Cor Violeta Azul Verde Amarelo Laranja Vermelho Comprimento de onda/nm
380‐450 450‐495 495‐570 570‐590 590‐620 620‐750 Tabela 2 DVD  650 Vermelho Blu‐ ray Disc 
1 10 Violeta 3,00
10
4,05
10 
7,40
10 
3,00 10
7,40 10
4,05
10
405 nm 5.3 Comente a seguinte afirmação: “Não se pode concluir que o laser utilizado na tecnologia Blu‐ ray Disc apresente, necessariamente, uma potência média maior do que o laser de um leitor de CD‐ROM” A frase está correcta, porque embora a frequência do laser do Blu‐ray Disc seja maior do que a frequência do laser do CD‐ROM, nada sabemos quanto à amplitude destes, e portanto nada podemos concluir quanto às respectivas energias. 6. Duas estrela X e Y têm temperaturas superficiais de 6000 K e 3000 K respectivamente. 6.1 Uma estrela pode apresentar diferentes cores consoante a temperatura a que se encontra. Associe as temperaturas indicadas na figura abaixo a cada uma das seguintes cores: amarelo; amarelo‐alaranjado; amarelo‐esbranquiçado; vermelho. 5 Figura 3 6000 K‐ Amarelo Esbranquiçado 5000 K ‐Amarelo 4000 K – Amarelo Alanjado 3000 K ‐ Vermelho 6.2 Qual é a cor de cada uma das estrela X e Y? X ‐ Amarelo Esbranquiçado Y ‐ Vermelho 6.3 Relacione as intensidades da radiações emitidas pelas duas estrelas X e Y. 
 6000  3000 

6000
3000
6000
3000
2
16 16
A intensidade da radiação emitida pela estrela X é 16 vezes maior do que a intensidade da radiação emitida pela estrela Y 6.4 Qual é o comprimento de onda correspondente à intensidade máxima irradiada pela estrela X? 

á
á ,
,
6.5 Qual é a potência da radiação emitida pela estrela X ( raio estrela X = 6,96 X 108 m)?  Considerar a área da superfície da estrela como a área de uma superfície esférica 4 5,67
4
10
6,96
6,09 10
10
6,09 6000
10
,
6.6 Será possível a estrela Y, mais fria, emitir a mesma potência de radiação do que a estrela X, mais quente? Justifique.  

3000
6000 6 6000 3000
6000
3000
2 16
OU 16
Em 6.3 vimos que 16
Então 16
Sim, se a área da superfície da estrela Y for 16 vezes maior do que a área da superfície a da estrela X 7. As estrelas são muitas vezes classificadas pela sua cor. O gráfico abaixo representa a intensidade da radiação emitida por uma estrela, a determinada temperatura, em função do comprimento de onda da radiação emitida. 290 Figura 4 7.1 Indique a cor da radiação visível emitida com maior intensidade pela estrela. Violeta (a radiação visível de maior intensidade é a radição na gama do visível de menor comprimento de onda porque no caso deste corpo, a uma determinada temperatura, a intensidade da radiação emitida na gama do visível aumenta para comprimentos de onda menores) 7.2 Calcule a temperatura da estrela. 
á
1 10 290
2,898 10
2,90 10
2,90
10 ,
7