Aplicações de Álgebra Linear

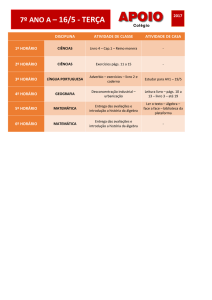
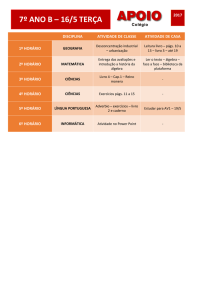
Aplicações de Álgebra Linear
Humberto José Bortolossi
Departamento de Matemática Aplicada
Universidade Federal Fluminense
Aula 1
6 de janeiro de 2010
1/62
Aula 1
Aplicações de Álgebra Linear
1/1
Apresentação
2/62
Aula 1
Aplicações de Álgebra Linear
1/1
Ementa
Revisão: base, transformação linear, núcleo, imagem, posto.
Métodos numéricos para resolução de sistemas lineares.
Ortogonalização, decomposição em valores singulares e aplicações.
Programação Linear: método simplex. Dualidade e teoria dos jogos.
3/62
Aula 1
Aplicações de Álgebra Linear
1/1
Bibliografia básica
Gilbert Strang. Linear Algebra and Its Applications. Third edition.
Thomson Learning, 1988.
Elon Lages Lima. Álgebra Linear. Coleção Matemática
Universitária. IMPA, 2008.
Flávio Ulhoa Coelho e Mary Lilian Lourenço. Um Curso de Álgebra
Linear. Editora da Universidade de São Paulo, 2002.
Grégoire Allaire and Sidi Mahmoud Kaber. Numerical Linear
Algebra. Springer-Verlag, 2008.
4/62
Aula 1
Aplicações de Álgebra Linear
1/1
Programação e Avaliação
Programação: O curso terá aulas expositivas com o instrutor às
segundas, quartas e sextas. As sessões de terça e quinta
serão realizadas com o monitor e consistirão de resolução
e discussão das listas de exercícios.
Avaliação: Baseada em duas provas e desempenho nas aulas e
sessões de discussão.
Datas das provas: 18/01/2010 e 01/02/2010.
Página WEB:
http://www.professores.uff.br/hjbortol/disciplinas/2010.1/fgv00000/
5/62
Aula 1
Aplicações de Álgebra Linear
1/2
Programação e Avaliação
Programação: O curso terá aulas expositivas com o instrutor às
segundas, quartas e sextas. As sessões de terça e quinta
serão realizadas com o monitor e consistirão de resolução
e discussão das listas de exercícios.
Avaliação: Baseada em duas provas e desempenho nas aulas e
sessões de discussão.
Datas das provas: 18/01/2010 e 01/02/2010.
Página WEB:
http://www.professores.uff.br/hjbortol/disciplinas/2010.1/fgv00000/
5/62
Aula 1
Aplicações de Álgebra Linear
2/2
Espaços Vetoriais
6/62
Aula 1
Aplicações de Álgebra Linear
1/1
Espaços vetoriais
Definição
Sejam:
(1) V 6= ∅
(conjunto de vetores),
(2) K = Q ou K = R ou K = C
(conjunto de escalares),
(3) + : V × V → V
(u, v) 7→ u + v
(adição de vetores),
(4)
7/62
· : K×V → V
(α, v) 7→ α · v
Aula 1
(multiplicação de vetor por escalar).
Aplicações de Álgebra Linear
1/4
Espaços vetoriais
Definição
Sejam:
(1) V 6= ∅
(conjunto de vetores),
(2) K = Q ou K = R ou K = C
(conjunto de escalares),
(3) + : V × V → V
(u, v) 7→ u + v
(adição de vetores),
(4)
7/62
· : K×V → V
(α, v) 7→ α · v
Aula 1
(multiplicação de vetor por escalar).
Aplicações de Álgebra Linear
2/4
Espaços vetoriais
Definição
Sejam:
(1) V 6= ∅
(conjunto de vetores),
(2) K = Q ou K = R ou K = C
(conjunto de escalares),
(3) + : V × V → V
(u, v) 7→ u + v
(adição de vetores),
(4)
7/62
· : K×V → V
(α, v) 7→ α · v
Aula 1
(multiplicação de vetor por escalar).
Aplicações de Álgebra Linear
3/4
Espaços vetoriais
Definição
Sejam:
(1) V 6= ∅
(conjunto de vetores),
(2) K = Q ou K = R ou K = C
(conjunto de escalares),
(3) + : V × V → V
(u, v) 7→ u + v
(adição de vetores),
(4)
7/62
· : K×V → V
(α, v) 7→ α · v
Aula 1
(multiplicação de vetor por escalar).
Aplicações de Álgebra Linear
4/4
Espaços vetoriais
Definição
Dizemos que (V , K, +, · ) é um espaço vetorial se as seguintes
condições forem satisfeitas ∀α, β ∈ K e ∀u, v, w ∈ V :
(A1)
(comutatividade)
u + v = v + u,
(A2)
(associatividade)
(u + v) + w = u + (v + w),
(A3)
(vetor nulo)
∃0 ∈ V tal que ∀v ∈ V , v + 0 = 0 + v = v,
(A4)
(inverso aditivo)
∀v ∈ V , ∃w ∈ V tal que v + w = w + v = 0,
[notações: w = −v e u − v = u + (−v)]
8/62
(M1)
(associatividade)
(α · β) · v = α · (β · v),
(M2)
(multiplicação por 1)
1 · v = v,
(D1)
(distributividade)
α · (u + v) = α · u + α · v,
(D2)
(distributividade)
(α + β) · v = α · v + β · v.
Aula 1
Aplicações de Álgebra Linear
1/4
Espaços vetoriais
Definição
Dizemos que (V , K, +, · ) é um espaço vetorial se as seguintes
condições forem satisfeitas ∀α, β ∈ K e ∀u, v, w ∈ V :
(A1)
(comutatividade)
u + v = v + u,
(A2)
(associatividade)
(u + v) + w = u + (v + w),
(A3)
(vetor nulo)
∃0 ∈ V tal que ∀v ∈ V , v + 0 = 0 + v = v,
(A4)
(inverso aditivo)
∀v ∈ V , ∃w ∈ V tal que v + w = w + v = 0,
[notações: w = −v e u − v = u + (−v)]
8/62
(M1)
(associatividade)
(α · β) · v = α · (β · v),
(M2)
(multiplicação por 1)
1 · v = v,
(D1)
(distributividade)
α · (u + v) = α · u + α · v,
(D2)
(distributividade)
(α + β) · v = α · v + β · v.
Aula 1
Aplicações de Álgebra Linear
2/4
Espaços vetoriais
Definição
Dizemos que (V , K, +, · ) é um espaço vetorial se as seguintes
condições forem satisfeitas ∀α, β ∈ K e ∀u, v, w ∈ V :
(A1)
(comutatividade)
u + v = v + u,
(A2)
(associatividade)
(u + v) + w = u + (v + w),
(A3)
(vetor nulo)
∃0 ∈ V tal que ∀v ∈ V , v + 0 = 0 + v = v,
(A4)
(inverso aditivo)
∀v ∈ V , ∃w ∈ V tal que v + w = w + v = 0,
[notações: w = −v e u − v = u + (−v)]
8/62
(M1)
(associatividade)
(α · β) · v = α · (β · v),
(M2)
(multiplicação por 1)
1 · v = v,
(D1)
(distributividade)
α · (u + v) = α · u + α · v,
(D2)
(distributividade)
(α + β) · v = α · v + β · v.
Aula 1
Aplicações de Álgebra Linear
3/4
Espaços vetoriais
Definição
Dizemos que (V , K, +, · ) é um espaço vetorial se as seguintes
condições forem satisfeitas ∀α, β ∈ K e ∀u, v, w ∈ V :
(A1)
(comutatividade)
u + v = v + u,
(A2)
(associatividade)
(u + v) + w = u + (v + w),
(A3)
(vetor nulo)
∃0 ∈ V tal que ∀v ∈ V , v + 0 = 0 + v = v,
(A4)
(inverso aditivo)
∀v ∈ V , ∃w ∈ V tal que v + w = w + v = 0,
[notações: w = −v e u − v = u + (−v)]
8/62
(M1)
(associatividade)
(α · β) · v = α · (β · v),
(M2)
(multiplicação por 1)
1 · v = v,
(D1)
(distributividade)
α · (u + v) = α · u + α · v,
(D2)
(distributividade)
(α + β) · v = α · v + β · v.
Aula 1
Aplicações de Álgebra Linear
4/4
Exemplo: Rn
V = Rn = {(v1 , . . . , vn ) | v1 ∈ R, . . . , vn ∈ R}
K=R
u + v = (u1 , . . . , un ) + (v1 , . . . , vn ) = (u1 + v1 , . . . , un + vn )
α · u = α · (u1 , . . . , un ) = (α · u1 , . . . , α · un )
0 = (0, . . . , 0)
− u = − (u1 , . . . , un ) = (−u1 , . . . , −un )
9/62
Aula 1
Aplicações de Álgebra Linear
1/6
Exemplo: Rn
V = Rn = {(v1 , . . . , vn ) | v1 ∈ R, . . . , vn ∈ R}
K=R
u + v = (u1 , . . . , un ) + (v1 , . . . , vn ) = (u1 + v1 , . . . , un + vn )
α · u = α · (u1 , . . . , un ) = (α · u1 , . . . , α · un )
0 = (0, . . . , 0)
− u = − (u1 , . . . , un ) = (−u1 , . . . , −un )
9/62
Aula 1
Aplicações de Álgebra Linear
2/6
Exemplo: Rn
V = Rn = {(v1 , . . . , vn ) | v1 ∈ R, . . . , vn ∈ R}
K=R
u + v = (u1 , . . . , un ) + (v1 , . . . , vn ) = (u1 + v1 , . . . , un + vn )
α · u = α · (u1 , . . . , un ) = (α · u1 , . . . , α · un )
0 = (0, . . . , 0)
− u = − (u1 , . . . , un ) = (−u1 , . . . , −un )
9/62
Aula 1
Aplicações de Álgebra Linear
3/6
Exemplo: Rn
V = Rn = {(v1 , . . . , vn ) | v1 ∈ R, . . . , vn ∈ R}
K=R
u + v = (u1 , . . . , un ) + (v1 , . . . , vn ) = (u1 + v1 , . . . , un + vn )
α · u = α · (u1 , . . . , un ) = (α · u1 , . . . , α · un )
0 = (0, . . . , 0)
− u = − (u1 , . . . , un ) = (−u1 , . . . , −un )
9/62
Aula 1
Aplicações de Álgebra Linear
4/6
Exemplo: Rn
V = Rn = {(v1 , . . . , vn ) | v1 ∈ R, . . . , vn ∈ R}
K=R
u + v = (u1 , . . . , un ) + (v1 , . . . , vn ) = (u1 + v1 , . . . , un + vn )
α · u = α · (u1 , . . . , un ) = (α · u1 , . . . , α · un )
0 = (0, . . . , 0)
− u = − (u1 , . . . , un ) = (−u1 , . . . , −un )
9/62
Aula 1
Aplicações de Álgebra Linear
5/6
Exemplo: Rn
V = Rn = {(v1 , . . . , vn ) | v1 ∈ R, . . . , vn ∈ R}
K=R
u + v = (u1 , . . . , un ) + (v1 , . . . , vn ) = (u1 + v1 , . . . , un + vn )
α · u = α · (u1 , . . . , un ) = (α · u1 , . . . , α · un )
0 = (0, . . . , 0)
− u = − (u1 , . . . , un ) = (−u1 , . . . , −un )
9/62
Aula 1
Aplicações de Álgebra Linear
6/6
Exemplo: o espaço das sequências reais
V = R∞ = {(v1 , . . . , vi , . . .) | v1 ∈ R, . . . , vi ∈ R, . . .}
K=R
u + v = (u1 , . . . , ui , . . .) + (v1 , . . . , vi , . . .) = (u1 + v1 , . . . , ui + vi , . . .)
α · u = α · (u1 , . . . , ui , . . .) = (α · u1 , . . . , α · ui , . . .)
0 = (0, . . . , 0, . . .)
− u = − (u1 , . . . , ui , . . .) = (−u1 , . . . , −ui , . . .)
10/62
Aula 1
Aplicações de Álgebra Linear
1/6
Exemplo: o espaço das sequências reais
V = R∞ = {(v1 , . . . , vi , . . .) | v1 ∈ R, . . . , vi ∈ R, . . .}
K=R
u + v = (u1 , . . . , ui , . . .) + (v1 , . . . , vi , . . .) = (u1 + v1 , . . . , ui + vi , . . .)
α · u = α · (u1 , . . . , ui , . . .) = (α · u1 , . . . , α · ui , . . .)
0 = (0, . . . , 0, . . .)
− u = − (u1 , . . . , ui , . . .) = (−u1 , . . . , −ui , . . .)
10/62
Aula 1
Aplicações de Álgebra Linear
2/6
Exemplo: o espaço das sequências reais
V = R∞ = {(v1 , . . . , vi , . . .) | v1 ∈ R, . . . , vi ∈ R, . . .}
K=R
u + v = (u1 , . . . , ui , . . .) + (v1 , . . . , vi , . . .) = (u1 + v1 , . . . , ui + vi , . . .)
α · u = α · (u1 , . . . , ui , . . .) = (α · u1 , . . . , α · ui , . . .)
0 = (0, . . . , 0, . . .)
− u = − (u1 , . . . , ui , . . .) = (−u1 , . . . , −ui , . . .)
10/62
Aula 1
Aplicações de Álgebra Linear
3/6
Exemplo: o espaço das sequências reais
V = R∞ = {(v1 , . . . , vi , . . .) | v1 ∈ R, . . . , vi ∈ R, . . .}
K=R
u + v = (u1 , . . . , ui , . . .) + (v1 , . . . , vi , . . .) = (u1 + v1 , . . . , ui + vi , . . .)
α · u = α · (u1 , . . . , ui , . . .) = (α · u1 , . . . , α · ui , . . .)
0 = (0, . . . , 0, . . .)
− u = − (u1 , . . . , ui , . . .) = (−u1 , . . . , −ui , . . .)
10/62
Aula 1
Aplicações de Álgebra Linear
4/6
Exemplo: o espaço das sequências reais
V = R∞ = {(v1 , . . . , vi , . . .) | v1 ∈ R, . . . , vi ∈ R, . . .}
K=R
u + v = (u1 , . . . , ui , . . .) + (v1 , . . . , vi , . . .) = (u1 + v1 , . . . , ui + vi , . . .)
α · u = α · (u1 , . . . , ui , . . .) = (α · u1 , . . . , α · ui , . . .)
0 = (0, . . . , 0, . . .)
− u = − (u1 , . . . , ui , . . .) = (−u1 , . . . , −ui , . . .)
10/62
Aula 1
Aplicações de Álgebra Linear
5/6
Exemplo: o espaço das sequências reais
V = R∞ = {(v1 , . . . , vi , . . .) | v1 ∈ R, . . . , vi ∈ R, . . .}
K=R
u + v = (u1 , . . . , ui , . . .) + (v1 , . . . , vi , . . .) = (u1 + v1 , . . . , ui + vi , . . .)
α · u = α · (u1 , . . . , ui , . . .) = (α · u1 , . . . , α · ui , . . .)
0 = (0, . . . , 0, . . .)
− u = − (u1 , . . . , ui , . . .) = (−u1 , . . . , −ui , . . .)
10/62
Aula 1
Aplicações de Álgebra Linear
6/6
Exemplo: o espaço das matrizes reais m × n






 a11 · · · a1n  ..

.
.
..
..  aij ∈ R para 1 ≤ i ≤ m e 1 ≤ j ≤ n
V = Mm×n (R) =  .




am1 · · · amn K=R

 
 

u11 · · · u1n
v11 · · · v1n
u11 + v11 · · · u1n + v1n


..  +  ..
..  = 
..
..
..
..
..
u + v =  ...

.
.
.
.   .
.  
.
.
um1 · · · umn
vm1 · · · vmn
um1 + vm1 · · · umn + vmn

 
u11 · · · u1n
α · u11 · · · α · u1n


..  = 
..
..
..
..
α · u = α ·  ...

.
.
.  
.
.
um1 · · · umn
α · um1 · · · α · umn

11/62
Aula 1
Aplicações de Álgebra Linear
1/3
Exemplo: o espaço das matrizes reais m × n






 a11 · · · a1n  ..

.
.
..
..  aij ∈ R para 1 ≤ i ≤ m e 1 ≤ j ≤ n
V = Mm×n (R) =  .




am1 · · · amn K=R

 
 

u11 · · · u1n
v11 · · · v1n
u11 + v11 · · · u1n + v1n


..  +  ..
..  = 
..
..
..
..
..
u + v =  ...

.
.
.
.   .
.  
.
.
um1 · · · umn
vm1 · · · vmn
um1 + vm1 · · · umn + vmn

 
u11 · · · u1n
α · u11 · · · α · u1n


..  = 
..
..
..
..
α · u = α ·  ...

.
.
.  
.
.
um1 · · · umn
α · um1 · · · α · umn

11/62
Aula 1
Aplicações de Álgebra Linear
2/3
Exemplo: o espaço das matrizes reais m × n






 a11 · · · a1n  ..

.
.
..
..  aij ∈ R para 1 ≤ i ≤ m e 1 ≤ j ≤ n
V = Mm×n (R) =  .




am1 · · · amn K=R

 
 

u11 · · · u1n
v11 · · · v1n
u11 + v11 · · · u1n + v1n


..  +  ..
..  = 
..
..
..
..
..
u + v =  ...

.
.
.
.   .
.  
.
.
um1 · · · umn
vm1 · · · vmn
um1 + vm1 · · · umn + vmn

 
u11 · · · u1n
α · u11 · · · α · u1n


..  = 
..
..
..
..
α · u = α ·  ...

.
.
.  
.
.
um1 · · · umn
α · um1 · · · α · umn

11/62
Aula 1
Aplicações de Álgebra Linear
3/3
Exemplo: o espaço das funções reais
V = F(X , R) = conjunto de todas as funções f de X em R com X 6= ∅
K=R
f + g:
X
x
α·f : X
x
12/62
Aula 1
→
7
→
R
(f + g)(x) = f (x) + g(x)
→ R
7
→
(α · f )(x) = α · f (x)
Aplicações de Álgebra Linear
1/6
Exemplo: o espaço das funções reais
V = F(X , R) = conjunto de todas as funções f de X em R com X 6= ∅
K=R
f + g:
X
x
α·f : X
x
12/62
Aula 1
→
7
→
R
(f + g)(x) = f (x) + g(x)
→ R
7
→
(α · f )(x) = α · f (x)
Aplicações de Álgebra Linear
2/6
Exemplo: o espaço das funções reais
V = F(X , R) = conjunto de todas as funções f de X em R com X 6= ∅
K=R
f + g:
X
x
α·f : X
x
12/62
Aula 1
→
7
→
R
(f + g)(x) = f (x) + g(x)
→ R
7
→
(α · f )(x) = α · f (x)
Aplicações de Álgebra Linear
3/6
Exemplo: o espaço das funções reais
V = F(X , R) = conjunto de todas as funções f de X em R com X 6= ∅
K=R
f + g:
X
x
α·f : X
x
12/62
Aula 1
→
7
→
R
(f + g)(x) = f (x) + g(x)
→ R
7
→
(α · f )(x) = α · f (x)
Aplicações de Álgebra Linear
4/6
Exemplo: o espaço das funções reais
V = F(X , R) = conjunto de todas as funções f de X em R com X 6= ∅
K=R
f + g:
X
x
α·f : X
x
12/62
Aula 1
→
7
→
R
(f + g)(x) = f (x) + g(x)
→ R
7
→
(α · f )(x) = α · f (x)
Aplicações de Álgebra Linear
5/6
Exemplo: o espaço das funções reais
V = F(X , R) = conjunto de todas as funções f de X em R com X 6= ∅
K=R
f + g:
X
x
α·f : X
x
12/62
Aula 1
→
7
→
R
(f + g)(x) = f (x) + g(x)
→ R
7
→
(α · f )(x) = α · f (x)
Aplicações de Álgebra Linear
6/6
Propriedades
(1) O vetor nulo é único.
(2) O inverso aditivo de um vetor é único.
(3) Se u + w = v + w, então u = v.
(4) 0 · v = 0 e α · 0 = 0.
(5) Se α 6= 0 e v 6= 0, então α · v 6= 0.
(6) (−1) · v = −v.
(7) −0 = 0.
(8) −(−v) = v.
13/62
Aula 1
Aplicações de Álgebra Linear
1/1
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
0
= 0
= 0.
14/62
Aula 1
Aplicações de Álgebra Linear
1/8
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
0
= 0
= 0.
14/62
Aula 1
Aplicações de Álgebra Linear
2/8
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
0
= 0
= 0.
14/62
Aula 1
Aplicações de Álgebra Linear
3/8
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
0
= 0
= 0.
14/62
Aula 1
Aplicações de Álgebra Linear
4/8
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
0
= 0
= 0.
14/62
Aula 1
Aplicações de Álgebra Linear
5/8
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
= 0.
0
= 0
14/62
Aula 1
Aplicações de Álgebra Linear
6/8
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
= 0.
0
= 0
14/62
Aula 1
Aplicações de Álgebra Linear
7/8
Demonstração da propriedade (1)
O vetor nulo de um espaço vetorial é único.
e dois vetores nulos do espaço vetorial. Temos
Demonstração. Considere 0 e 0
que:
e (A3)
e + 0 (A3)
0
= 0
= 0.
14/62
Aula 1
Aplicações de Álgebra Linear
8/8
Exercício
Mostre que o inverso aditivo de um elemento v é único:
v+w=w+v=0
e
⇒ w = w.
e =w
e +v=0
v+w
15/62
Aula 1
Aplicações de Álgebra Linear
1/7
Exercício
Mostre que o inverso aditivo de um elemento v é único:
v+w=w+v=0
e
⇒ w = w.
e =w
e +v=0
v+w
Demonstração.
15/62
Aula 1
Aplicações de Álgebra Linear
2/7
Exercício
Mostre que o inverso aditivo de um elemento v é único:
v+w=w+v=0
e
⇒ w = w.
e =w
e +v=0
v+w
Demonstração. Temos que
w=0+w
15/62
Aula 1
Aplicações de Álgebra Linear
3/7
Exercício
Mostre que o inverso aditivo de um elemento v é único:
v+w=w+v=0
e
⇒ w = w.
e =w
e +v=0
v+w
Demonstração. Temos que
e + v) + w
w = 0 + w = (w
15/62
Aula 1
Aplicações de Álgebra Linear
4/7
Exercício
Mostre que o inverso aditivo de um elemento v é único:
v+w=w+v=0
e
⇒ w = w.
e =w
e +v=0
v+w
Demonstração. Temos que
e + v) + w = w
e + (v + w)
w = 0 + w = (w
15/62
Aula 1
Aplicações de Álgebra Linear
5/7
Exercício
Mostre que o inverso aditivo de um elemento v é único:
v+w=w+v=0
e
⇒ w = w.
e =w
e +v=0
v+w
Demonstração. Temos que
e + v) + w = w
e + (v + w) = w
e +0
w = 0 + w = (w
15/62
Aula 1
Aplicações de Álgebra Linear
6/7
Exercício
Mostre que o inverso aditivo de um elemento v é único:
v+w=w+v=0
e
⇒ w = w.
e =w
e +v=0
v+w
Demonstração. Temos que
e + v) + w = w
e + (v + w) = w
e + 0 = w.
e
w = 0 + w = (w
15/62
Aula 1
Aplicações de Álgebra Linear
7/7
Subespaços Vetoriais
16/62
Aula 1
Aplicações de Álgebra Linear
1/1
Subespaços vetoriais
Definição
Sejam (V , K, +, · ) um espaço vetorial. Um subespaço vetorial de V
é um subconjunto W ⊆ V com as seguintes propriedades:
(1) 0 ∈ W .
(2) Se w1 , w2 ∈ W , então w1 + w2 ∈ W .
(3) Se α ∈ K e w ∈ W , então α · w ∈ W .
Note que, em particular, W , K, +|W ×W , · |K×W é, em si mesmo, um espaço vetorial.
{0} e V são sempre subespaços de V , para qualquer espaço vetorial V .
17/62
Aula 1
Aplicações de Álgebra Linear
1/3
Subespaços vetoriais
Definição
Sejam (V , K, +, · ) um espaço vetorial. Um subespaço vetorial de V
é um subconjunto W ⊆ V com as seguintes propriedades:
(1) 0 ∈ W .
(2) Se w1 , w2 ∈ W , então w1 + w2 ∈ W .
(3) Se α ∈ K e w ∈ W , então α · w ∈ W .
Note que, em particular, W , K, +|W ×W , · |K×W é, em si mesmo, um espaço vetorial.
{0} e V são sempre subespaços de V , para qualquer espaço vetorial V .
17/62
Aula 1
Aplicações de Álgebra Linear
2/3
Subespaços vetoriais
Definição
Sejam (V , K, +, · ) um espaço vetorial. Um subespaço vetorial de V
é um subconjunto W ⊆ V com as seguintes propriedades:
(1) 0 ∈ W .
(2) Se w1 , w2 ∈ W , então w1 + w2 ∈ W .
(3) Se α ∈ K e w ∈ W , então α · w ∈ W .
Note que, em particular, W , K, +|W ×W , · |K×W é, em si mesmo, um espaço vetorial.
{0} e V são sempre subespaços de V , para qualquer espaço vetorial V .
17/62
Aula 1
Aplicações de Álgebra Linear
3/3
Exemplos
(1) W = {(v1 , v2 , . . . , vn ) ∈ Rn | v1 = 0} é subespaço de Rn .
(2) W = {A ∈ Mn×n (R) | A = AT } (conjunto das matrizes reais
simétricas) é subespaço de Mn×n (R).
(3) W = {f ∈ F(R, R) | f é contínua} (conjunto das funções reais
contínuas) é subespaço de F(R, R).

a11 · x1 + · · · + a1n · xn = 0,


..
(4) W =
(x1 , . . . , xn ) ∈ Rn .


am1 · x1 + · · · + amn · xn = 0.
(soluções de um sistema linear homogêneo) é subespaço de Rn .
18/62
Aula 1
Aplicações de Álgebra Linear





1/4
Exemplos
(1) W = {(v1 , v2 , . . . , vn ) ∈ Rn | v1 = 0} é subespaço de Rn .
(2) W = {A ∈ Mn×n (R) | A = AT } (conjunto das matrizes reais
simétricas) é subespaço de Mn×n (R).
(3) W = {f ∈ F(R, R) | f é contínua} (conjunto das funções reais
contínuas) é subespaço de F(R, R).

a11 · x1 + · · · + a1n · xn = 0,


..
(4) W =
(x1 , . . . , xn ) ∈ Rn .


am1 · x1 + · · · + amn · xn = 0.
(soluções de um sistema linear homogêneo) é subespaço de Rn .
18/62
Aula 1
Aplicações de Álgebra Linear





2/4
Exemplos
(1) W = {(v1 , v2 , . . . , vn ) ∈ Rn | v1 = 0} é subespaço de Rn .
(2) W = {A ∈ Mn×n (R) | A = AT } (conjunto das matrizes reais
simétricas) é subespaço de Mn×n (R).
(3) W = {f ∈ F(R, R) | f é contínua} (conjunto das funções reais
contínuas) é subespaço de F(R, R).

a11 · x1 + · · · + a1n · xn = 0,


..
(4) W =
(x1 , . . . , xn ) ∈ Rn .


am1 · x1 + · · · + amn · xn = 0.
(soluções de um sistema linear homogêneo) é subespaço de Rn .
18/62
Aula 1
Aplicações de Álgebra Linear





3/4
Exemplos
(1) W = {(v1 , v2 , . . . , vn ) ∈ Rn | v1 = 0} é subespaço de Rn .
(2) W = {A ∈ Mn×n (R) | A = AT } (conjunto das matrizes reais
simétricas) é subespaço de Mn×n (R).
(3) W = {f ∈ F(R, R) | f é contínua} (conjunto das funções reais
contínuas) é subespaço de F(R, R).

a11 · x1 + · · · + a1n · xn = 0,


..
(4) W =
(x1 , . . . , xn ) ∈ Rn .


am1 · x1 + · · · + amn · xn = 0.
(soluções de um sistema linear homogêneo) é subespaço de Rn .
18/62
Aula 1
Aplicações de Álgebra Linear





4/4
Exercício
W1 = {A ∈ Mn×n (R) | tr(A) = 0}
e
W2 = {A ∈ Mn×n (R) | tr(A) 6= 0}
são subespaços vetoriais de V = Mn×n (R)?


a11 · · · a1n
n

..  = a + a + · · · + a = X a .
..
tr  ...


nn
.
11
22
ii
.
i=1
an1 · · · ann
19/62
Aula 1
Aplicações de Álgebra Linear
1/1
Operações com Subespaços
20/62
Aula 1
Aplicações de Álgebra Linear
1/1
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
1/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
2/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
3/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
4/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
5/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
6/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
7/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
8/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
9/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
10/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
11/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
12/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
13/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
14/15
Interseção
Teorema
Seja {Wλ }λ∈Λ uma coleção de subespaços de um espaço vetorial V .
Então, a interseção
\
W =
Wλ
λ∈Λ
também é um subespaço de V .
Demonstração.
(1) Para todo λ ∈ Λ, temos que 0 ∈ Wλ , pois cada Wλ é subespaço vetorial
T
de V . Logo, 0 ∈ W = λ∈Λ Wλ .
T
(2) Se w1 , w2 ∈ W = λ∈Λ Wλ , então w1 , w2 ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaçoTvetorial, segue-se que w1 + w2 ∈ Wλ , ∀λ ∈ Λ.
Logo, w1 + w2 ∈ W = λ∈Λ Wλ .
T
(3) Se α ∈ K e w ∈ W = λ∈Λ Wλ , então w ∈ Wλ , para todo λ ∈ Λ. Como
cada Wλ é subespaço
vetorial, segue-se que α · w ∈ Wλ , ∀λ ∈ Λ. Logo,
T
α · w ∈ W = λ∈Λ Wλ .
21/62
Aula 1
Aplicações de Álgebra Linear
15/15
União
União de subespaços não é, em geral, um subespaço.
W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}
são subespaços de R2 .
Mas W = W1 ∪ W2 não é subespaço de R2 .
De fato: w1 = (1, 0) ∈ W , w2 = (0, 1) ∈ W ,
mas w = w1 + w2 = (1, 1) 6∈ W .
22/62
Aula 1
Aplicações de Álgebra Linear
1/5
União
União de subespaços não é, em geral, um subespaço.
W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}
são subespaços de R2 .
Mas W = W1 ∪ W2 não é subespaço de R2 .
De fato: w1 = (1, 0) ∈ W , w2 = (0, 1) ∈ W ,
mas w = w1 + w2 = (1, 1) 6∈ W .
22/62
Aula 1
Aplicações de Álgebra Linear
2/5
União
União de subespaços não é, em geral, um subespaço.
W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}
são subespaços de R2 .
Mas W = W1 ∪ W2 não é subespaço de R2 .
De fato: w1 = (1, 0) ∈ W , w2 = (0, 1) ∈ W ,
mas w = w1 + w2 = (1, 1) 6∈ W .
22/62
Aula 1
Aplicações de Álgebra Linear
3/5
União
União de subespaços não é, em geral, um subespaço.
W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}
são subespaços de R2 .
Mas W = W1 ∪ W2 não é subespaço de R2 .
De fato: w1 = (1, 0) ∈ W , w2 = (0, 1) ∈ W ,
mas w = w1 + w2 = (1, 1) 6∈ W .
22/62
Aula 1
Aplicações de Álgebra Linear
4/5
União
União de subespaços não é, em geral, um subespaço.
W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}
são subespaços de R2 .
Mas W = W1 ∪ W2 não é subespaço de R2 .
De fato: w1 = (1, 0) ∈ W , w2 = (0, 1) ∈ W ,
mas w = w1 + w2 = (1, 1) 6∈ W .
22/62
Aula 1
Aplicações de Álgebra Linear
5/5
Soma
Teorema
Sejam W1 e W2 dois subespaços de um espaço vetorial V . Então,
a soma
W = W1 + W2 = {w1 + w2 ∈ V | w1 ∈ W1 e w2 ∈ W2 }
também é um subespaço de V .
23/62
Aula 1
Aplicações de Álgebra Linear
1/1
Soma direta
Definição
Dizemos que W é soma direta dos subespaços W1 e W2 se
W1 + W2 = W
e
W1 ∩ W2 = {0}.
Notação: W = W1 ⊕ W2 .
24/62
Aula 1
Aplicações de Álgebra Linear
1/1
Exemplos
(1) W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}.
e
W2 = {A ∈ Mn×n (K) | A = −AT }.
e
W2 = {f ∈ F(R, R) | f é ímpar}.
R2 = W1 ⊕ W2
(2) W1 = {A ∈ Mn×n (K) | A = AT }
Mn×n (K) = W1 ⊕ W2
(3) W1 = {f ∈ F(R, R) | f é par}
F(R, R) = W1 ⊕ W2
25/62
Aula 1
Aplicações de Álgebra Linear
1/3
Exemplos
(1) W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}.
e
W2 = {A ∈ Mn×n (K) | A = −AT }.
e
W2 = {f ∈ F(R, R) | f é ímpar}.
R2 = W1 ⊕ W2
(2) W1 = {A ∈ Mn×n (K) | A = AT }
Mn×n (K) = W1 ⊕ W2
(3) W1 = {f ∈ F(R, R) | f é par}
F(R, R) = W1 ⊕ W2
25/62
Aula 1
Aplicações de Álgebra Linear
2/3
Exemplos
(1) W1 = {(x, 0) ∈ R2 | x ∈ R}
e
W2 = {(0, y ) ∈ R2 | y ∈ R}.
e
W2 = {A ∈ Mn×n (K) | A = −AT }.
e
W2 = {f ∈ F(R, R) | f é ímpar}.
R2 = W1 ⊕ W2
(2) W1 = {A ∈ Mn×n (K) | A = AT }
Mn×n (K) = W1 ⊕ W2
(3) W1 = {f ∈ F(R, R) | f é par}
F(R, R) = W1 ⊕ W2
25/62
Aula 1
Aplicações de Álgebra Linear
3/3
Soma direta
Definição
W = W1 ⊕ · · · ⊕ Wk
m
26/62




W = W1 + · · · + Wk



∀1 ≤ j ≤ k , Wj ∩ (W1 + · · · + Wj−1 + Wj+1 + · · · Wk ) = {0}.
e
Aula 1
Aplicações de Álgebra Linear
1/1
Combinações Lineares e Geradores
27/62
Aula 1
Aplicações de Álgebra Linear
1/1
Combinações Lineares e Geradores
Definição
Seja V um espaço vetorial.
(1) Um vetor v ∈ V é uma combinação linear dos vetores
v1 , . . . , vk ∈ V se existem escalares α1 , . . . , αk ∈ K tais que
v = α1 · v1 + · · · + αk · vk =
k
X
αi · vi .
i=1
(2) Seja B um subconjunto de V . O subespaço gerado por B,
denotado por [B], é o conjunto formado por todo todo elemento
de V que é uma combinação linear de um número finito de
elementos de B. Convenção: [∅] = {0}.
(3) Se [B] = V , dizemos que B é um conjunto de geradores de V .
Exercício: mostre que, de fato, [B] é subespaço vetorial de V .
28/62
Aula 1
Aplicações de Álgebra Linear
1/6
Combinações Lineares e Geradores
Definição
Seja V um espaço vetorial.
(1) Um vetor v ∈ V é uma combinação linear dos vetores
v1 , . . . , vk ∈ V se existem escalares α1 , . . . , αk ∈ K tais que
v = α1 · v1 + · · · + αk · vk =
k
X
αi · vi .
i=1
(2) Seja B um subconjunto de V . O subespaço gerado por B,
denotado por [B], é o conjunto formado por todo todo elemento
de V que é uma combinação linear de um número finito de
elementos de B. Convenção: [∅] = {0}.
(3) Se [B] = V , dizemos que B é um conjunto de geradores de V .
Exercício: mostre que, de fato, [B] é subespaço vetorial de V .
28/62
Aula 1
Aplicações de Álgebra Linear
2/6
Combinações Lineares e Geradores
Definição
Seja V um espaço vetorial.
(1) Um vetor v ∈ V é uma combinação linear dos vetores
v1 , . . . , vk ∈ V se existem escalares α1 , . . . , αk ∈ K tais que
v = α1 · v1 + · · · + αk · vk =
k
X
αi · vi .
i=1
(2) Seja B um subconjunto de V . O subespaço gerado por B,
denotado por [B], é o conjunto formado por todo todo elemento
de V que é uma combinação linear de um número finito de
elementos de B. Convenção: [∅] = {0}.
(3) Se [B] = V , dizemos que B é um conjunto de geradores de V .
Exercício: mostre que, de fato, [B] é subespaço vetorial de V .
28/62
Aula 1
Aplicações de Álgebra Linear
3/6
Combinações Lineares e Geradores
Definição
Seja V um espaço vetorial.
(1) Um vetor v ∈ V é uma combinação linear dos vetores
v1 , . . . , vk ∈ V se existem escalares α1 , . . . , αk ∈ K tais que
v = α1 · v1 + · · · + αk · vk =
k
X
αi · vi .
i=1
(2) Seja B um subconjunto de V . O subespaço gerado por B,
denotado por [B], é o conjunto formado por todo todo elemento
de V que é uma combinação linear de um número finito de
elementos de B. Convenção: [∅] = {0}.
(3) Se [B] = V , dizemos que B é um conjunto de geradores de V .
Exercício: mostre que, de fato, [B] é subespaço vetorial de V .
28/62
Aula 1
Aplicações de Álgebra Linear
4/6
Combinações Lineares e Geradores
Definição
Seja V um espaço vetorial.
(1) Um vetor v ∈ V é uma combinação linear dos vetores
v1 , . . . , vk ∈ V se existem escalares α1 , . . . , αk ∈ K tais que
v = α1 · v1 + · · · + αk · vk =
k
X
αi · vi .
i=1
(2) Seja B um subconjunto de V . O subespaço gerado por B,
denotado por [B], é o conjunto formado por todo todo elemento
de V que é uma combinação linear de um número finito de
elementos de B. Convenção: [∅] = {0}.
(3) Se [B] = V , dizemos que B é um conjunto de geradores de V .
Exercício: mostre que, de fato, [B] é subespaço vetorial de V .
28/62
Aula 1
Aplicações de Álgebra Linear
5/6
Combinações Lineares e Geradores
Definição
Seja V um espaço vetorial.
(1) Um vetor v ∈ V é uma combinação linear dos vetores
v1 , . . . , vk ∈ V se existem escalares α1 , . . . , αk ∈ K tais que
v = α1 · v1 + · · · + αk · vk =
k
X
αi · vi .
i=1
(2) Seja B um subconjunto de V . O subespaço gerado por B,
denotado por [B], é o conjunto formado por todo todo elemento
de V que é uma combinação linear de um número finito de
elementos de B. Convenção: [∅] = {0}.
(3) Se [B] = V , dizemos que B é um conjunto de geradores de V .
Exercício: mostre que, de fato, [B] é subespaço vetorial de V .
28/62
Aula 1
Aplicações de Álgebra Linear
6/6
Exemplos
(1) [(1, 0), (0, 1)] = R2 .
(2) [(1, 0), (0, 1), (1, 1)] = R2 .
(3) [R2 ] = R2 .
(4) [1, x, . . . , x n , . . .] = P(R), onde P(R) é o espaço vetorial dos polinômios com
coeficientes reais .
29/62
Aula 1
Aplicações de Álgebra Linear
1/4
Exemplos
(1) [(1, 0), (0, 1)] = R2 .
(2) [(1, 0), (0, 1), (1, 1)] = R2 .
(3) [R2 ] = R2 .
(4) [1, x, . . . , x n , . . .] = P(R), onde P(R) é o espaço vetorial dos polinômios com
coeficientes reais .
29/62
Aula 1
Aplicações de Álgebra Linear
2/4
Exemplos
(1) [(1, 0), (0, 1)] = R2 .
(2) [(1, 0), (0, 1), (1, 1)] = R2 .
(3) [R2 ] = R2 .
(4) [1, x, . . . , x n , . . .] = P(R), onde P(R) é o espaço vetorial dos polinômios com
coeficientes reais .
29/62
Aula 1
Aplicações de Álgebra Linear
3/4
Exemplos
(1) [(1, 0), (0, 1)] = R2 .
(2) [(1, 0), (0, 1), (1, 1)] = R2 .
(3) [R2 ] = R2 .
(4) [1, x, . . . , x n , . . .] = P(R), onde P(R) é o espaço vetorial dos polinômios com
coeficientes reais .
29/62
Aula 1
Aplicações de Álgebra Linear
4/4
Combinações lineares e sistemas lineares


 a11 · x1 + · · · + a1n · xn = b1 ,
..
.


am1 · x1 + · · · + amn · xn = bm .
m



 
a11
a1n



 
x1 ·  ...  + · · · + xn ·  ...  = 
am1
amn

b1
.. 
. 
bm
Moral:
o sistema linear possui solução
m
o vetor (b1 , . . . , bm ) pode ser escrito como combinação linear
dos vetores (a11 , . . . , am1 ), . . . , (a1n , . . . , amn ).
30/62
Aula 1
Aplicações de Álgebra Linear
1/4
Combinações lineares e sistemas lineares


 a11 · x1 + · · · + a1n · xn = b1 ,
..
.


am1 · x1 + · · · + amn · xn = bm .
m

 
a11
a1n

 


x1 ·  ...  + · · · + xn ·  ...  = 
amn
am1



b1
.. 
. 
bm
Moral:
o sistema linear possui solução
m
o vetor (b1 , . . . , bm ) pode ser escrito como combinação linear
dos vetores (a11 , . . . , am1 ), . . . , (a1n , . . . , amn ).
30/62
Aula 1
Aplicações de Álgebra Linear
2/4
Combinações lineares e sistemas lineares


 a11 · x1 + · · · + a1n · xn = b1 ,
..
.


am1 · x1 + · · · + amn · xn = bm .
m

 
a11
a1n

 


x1 ·  ...  + · · · + xn ·  ...  = 
amn
am1



b1
.. 
. 
bm
Moral:
o sistema linear possui solução
m
o vetor (b1 , . . . , bm ) pode ser escrito como combinação linear
dos vetores (a11 , . . . , am1 ), . . . , (a1n , . . . , amn ).
30/62
Aula 1
Aplicações de Álgebra Linear
3/4
Combinações lineares e sistemas lineares


 a11 · x1 + · · · + a1n · xn = b1 ,
..
.


am1 · x1 + · · · + amn · xn = bm .
m

 
a11
a1n

 


x1 ·  ...  + · · · + xn ·  ...  = 
amn
am1



b1
.. 
. 
bm
Moral:
o sistema linear possui solução
m
o vetor (b1 , . . . , bm ) pode ser escrito como combinação linear
dos vetores (a11 , . . . , am1 ), . . . , (a1n , . . . , amn ).
30/62
Aula 1
Aplicações de Álgebra Linear
4/4
Multiplicação de matrizes e combinações lineares
ym×1 = Bm×r · xr ×1
m




y1
..
.
ym


 
=
 
 
|
b1
|
···
|
br
|
 
·
 
x1
..
.
xr




m




y1
..
.
ym




 = x1 · 



|
b1
|




 + · · · + xr · 


|
br
|



Moral:
Se y = B · x, então y é combinação linear das colunas da
matriz B.
31/62
Aula 1
Aplicações de Álgebra Linear
1/4
Multiplicação de matrizes e combinações lineares
ym×1 = Bm×r · xr ×1
m




y1
..
.
ym


 
=
 
 
|
b1
|
···
|
br
|
 
·
 
x1
..
.
xr




m




y1
..
.
ym




 = x1 · 



|
b1
|



 + · · · + xr · 



|
br
|



Moral:
Se y = B · x, então y é combinação linear das colunas da
matriz B.
31/62
Aula 1
Aplicações de Álgebra Linear
2/4
Multiplicação de matrizes e combinações lineares
ym×1 = Bm×r · xr ×1
m




y1
..
.
ym


 
=
 
 
|
b1
|
···
|
br
|
 
·
 
x1
..
.
xr




m




y1
..
.
ym




 = x1 · 



|
b1
|



 + · · · + xr · 



|
br
|



Moral:
Se y = B · x, então y é combinação linear das colunas da
matriz B.
31/62
Aula 1
Aplicações de Álgebra Linear
3/4
Multiplicação de matrizes e combinações lineares
ym×1 = Bm×r · xr ×1
m




y1
..
.
ym


 
=
 
 
|
b1
|
···
|
br
|
 
·
 
x1
..
.
xr




m




y1
..
.
ym




 = x1 · 



|
b1
|



 + · · · + xr · 



|
br
|



Moral:
Se y = B · x, então y é combinação linear das colunas da
matriz B.
31/62
Aula 1
Aplicações de Álgebra Linear
4/4
Multiplicação de matrizes e combinações lineares
Am×n = Bm×r · Cr ×n
m





|
a1
|
|
an
|
···

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c11
..
.
···
cr 1
c1r
..
.
crn




m





|
aj
|

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c1j
..
.
cr j




Moral:
Se A = B · C, então as colunas da matriz A são combinações
lineares das colunas da matriz B.
32/62
Aula 1
Aplicações de Álgebra Linear
1/4
Multiplicação de matrizes e combinações lineares
Am×n = Bm×r · Cr ×n
m





|
a1
|
|
an
|
···

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c11
..
.
···
c1r
..
.
crn
cr 1




m





|
aj
|

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c1j
..
.
cr j




Moral:
Se A = B · C, então as colunas da matriz A são combinações
lineares das colunas da matriz B.
32/62
Aula 1
Aplicações de Álgebra Linear
2/4
Multiplicação de matrizes e combinações lineares
Am×n = Bm×r · Cr ×n
m





|
a1
|
|
an
|
···

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c11
..
.
···
c1r
..
.
crn
cr 1




m





|
aj
|

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c1j
..
.
cr j




Moral:
Se A = B · C, então as colunas da matriz A são combinações
lineares das colunas da matriz B.
32/62
Aula 1
Aplicações de Álgebra Linear
3/4
Multiplicação de matrizes e combinações lineares
Am×n = Bm×r · Cr ×n
m





|
a1
|
|
an
|
···

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c11
..
.
···
c1r
..
.
crn
cr 1




m





|
aj
|

 
=
 
 
|
b1
|
···
|
br
|
 
·
 
c1j
..
.
cr j




Moral:
Se A = B · C, então as colunas da matriz A são combinações
lineares das colunas da matriz B.
32/62
Aula 1
Aplicações de Álgebra Linear
4/4
Geradores e a escolha de K
B = {(1, 0), (0, 1)}
é um conjunto gerador de V = C2
sobre K = C.
De fato: ∀(z1 , z2 ) ∈ C2 , (z1 , z2 ) = z1 · (1, 0) + z2 · (0, 1).
Mas
B = {(1, 0), (0, 1)} não é um conjunto gerador de V = C2
sobre K = R.
Por exemplo, (i, 0) 6∈ [(1, 0), (0, 1)].
B = {(1, 0), (0, 1), (i, 0), (0, i)} é um conjunto gerador de V = C2 sobre K = R.
33/62
Aula 1
Aplicações de Álgebra Linear
1/7
Geradores e a escolha de K
B = {(1, 0), (0, 1)}
é um conjunto gerador de V = C2
sobre K = C.
De fato: ∀(z1 , z2 ) ∈ C2 , (z1 , z2 ) = z1 · (1, 0) + z2 · (0, 1).
Mas
B = {(1, 0), (0, 1)} não é um conjunto gerador de V = C2
sobre K = R.
Por exemplo, (i, 0) 6∈ [(1, 0), (0, 1)].
B = {(1, 0), (0, 1), (i, 0), (0, i)} é um conjunto gerador de V = C2 sobre K = R.
33/62
Aula 1
Aplicações de Álgebra Linear
2/7
Geradores e a escolha de K
B = {(1, 0), (0, 1)}
é um conjunto gerador de V = C2
sobre K = C.
De fato: ∀(z1 , z2 ) ∈ C2 , (z1 , z2 ) = z1 · (1, 0) + z2 · (0, 1).
Mas
B = {(1, 0), (0, 1)} não é um conjunto gerador de V = C2
sobre K = R.
Por exemplo, (i, 0) 6∈ [(1, 0), (0, 1)].
B = {(1, 0), (0, 1), (i, 0), (0, i)} é um conjunto gerador de V = C2 sobre K = R.
33/62
Aula 1
Aplicações de Álgebra Linear
3/7
Geradores e a escolha de K
B = {(1, 0), (0, 1)}
é um conjunto gerador de V = C2
sobre K = C.
De fato: ∀(z1 , z2 ) ∈ C2 , (z1 , z2 ) = z1 · (1, 0) + z2 · (0, 1).
Mas
B = {(1, 0), (0, 1)} não é um conjunto gerador de V = C2
sobre K = R.
Por exemplo, (i, 0) 6∈ [(1, 0), (0, 1)].
B = {(1, 0), (0, 1), (i, 0), (0, i)} é um conjunto gerador de V = C2 sobre K = R.
33/62
Aula 1
Aplicações de Álgebra Linear
4/7
Geradores e a escolha de K
B = {(1, 0), (0, 1)}
é um conjunto gerador de V = C2
sobre K = C.
De fato: ∀(z1 , z2 ) ∈ C2 , (z1 , z2 ) = z1 · (1, 0) + z2 · (0, 1).
Mas
B = {(1, 0), (0, 1)} não é um conjunto gerador de V = C2
sobre K = R.
Por exemplo, (i, 0) 6∈ [(1, 0), (0, 1)].
B = {(1, 0), (0, 1), (i, 0), (0, i)} é um conjunto gerador de V = C2 sobre K = R.
33/62
Aula 1
Aplicações de Álgebra Linear
5/7
Geradores e a escolha de K
B = {(1, 0), (0, 1)}
é um conjunto gerador de V = C2
sobre K = C.
De fato: ∀(z1 , z2 ) ∈ C2 , (z1 , z2 ) = z1 · (1, 0) + z2 · (0, 1).
Mas
B = {(1, 0), (0, 1)} não é um conjunto gerador de V = C2
sobre K = R.
Por exemplo, (i, 0) 6∈ [(1, 0), (0, 1)].
B = {(1, 0), (0, 1), (i, 0), (0, i)} é um conjunto gerador de V = C2 sobre K = R.
33/62
Aula 1
Aplicações de Álgebra Linear
6/7
Geradores e a escolha de K
B = {(1, 0), (0, 1)}
é um conjunto gerador de V = C2
sobre K = C.
De fato: ∀(z1 , z2 ) ∈ C2 , (z1 , z2 ) = z1 · (1, 0) + z2 · (0, 1).
Mas
B = {(1, 0), (0, 1)} não é um conjunto gerador de V = C2
sobre K = R.
Por exemplo, (i, 0) 6∈ [(1, 0), (0, 1)].
B = {(1, 0), (0, 1), (i, 0), (0, i)} é um conjunto gerador de V = C2 sobre K = R.
33/62
Aula 1
Aplicações de Álgebra Linear
7/7
Bases
34/62
Aula 1
Aplicações de Álgebra Linear
1/1
Dependência e independência linear
Definição
Sejam (V , K, +, · ) um espaço vetorial e B um subconjunto de V .
(1) Dizemos que B é um conjunto linearmente independente (LI) se,
para qualquer escolha de vetores v1 , . . . , vk ∈ B tais que
α1 · v1 + · · · + αk · vk = 0
⇒
α1 = · · · = αk = 0,
onde α1 , . . . , αk ∈ K. Por convenção, ∅ é LI.
(2) Dizemos que B é linearmente dependente (LD) se ele não for LI.
35/62
Aula 1
Aplicações de Álgebra Linear
1/6
Dependência e independência linear
Definição
Sejam (V , K, +, · ) um espaço vetorial e B um subconjunto de V .
(1) Dizemos que B é um conjunto linearmente independente (LI) se,
para qualquer escolha de vetores v1 , . . . , vk ∈ B tais que
α1 · v1 + · · · + αk · vk = 0
⇒
α1 = · · · = αk = 0,
onde α1 , . . . , αk ∈ K. Por convenção, ∅ é LI.
(2) Dizemos que B é linearmente dependente (LD) se ele não for LI.
35/62
Aula 1
Aplicações de Álgebra Linear
2/6
Dependência e independência linear
Definição
Sejam (V , K, +, · ) um espaço vetorial e B um subconjunto de V .
(1) Dizemos que B é um conjunto linearmente independente (LI) se,
para qualquer escolha de vetores v1 , . . . , vk ∈ B tais que
α1 · v1 + · · · + αk · vk = 0
⇒
α1 = · · · = αk = 0,
onde α1 , . . . , αk ∈ K. Por convenção, ∅ é LI.
(2) Dizemos que B é linearmente dependente (LD) se ele não for LI.
35/62
Aula 1
Aplicações de Álgebra Linear
3/6
Dependência e independência linear
Definição
Sejam (V , K, +, · ) um espaço vetorial e B um subconjunto de V .
(1) Dizemos que B é um conjunto linearmente independente (LI) se,
para qualquer escolha de vetores v1 , . . . , vk ∈ B tais que
α1 · v1 + · · · + αk · vk = 0
⇒
α1 = · · · = αk = 0,
onde α1 , . . . , αk ∈ K. Por convenção, ∅ é LI.
(2) Dizemos que B é linearmente dependente (LD) se ele não for LI.
35/62
Aula 1
Aplicações de Álgebra Linear
4/6
Dependência e independência linear
Definição
Sejam (V , K, +, · ) um espaço vetorial e B um subconjunto de V .
(1) Dizemos que B é um conjunto linearmente independente (LI) se,
para qualquer escolha de vetores v1 , . . . , vk ∈ B tais que
α1 · v1 + · · · + αk · vk = 0
⇒
α1 = · · · = αk = 0,
onde α1 , . . . , αk ∈ K. Por convenção, ∅ é LI.
(2) Dizemos que B é linearmente dependente (LD) se ele não for LI.
35/62
Aula 1
Aplicações de Álgebra Linear
5/6
Dependência e independência linear
Definição
Sejam (V , K, +, · ) um espaço vetorial e B um subconjunto de V .
(1) Dizemos que B é um conjunto linearmente independente (LI) se,
para qualquer escolha de vetores v1 , . . . , vk ∈ B tais que
α1 · v1 + · · · + αk · vk = 0
⇒
α1 = · · · = αk = 0,
onde α1 , . . . , αk ∈ K. Por convenção, ∅ é LI.
(2) Dizemos que B é linearmente dependente (LD) se ele não for LI.
35/62
Aula 1
Aplicações de Álgebra Linear
6/6
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
1/8
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
2/8
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
3/8
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
4/8
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
5/8
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
6/8
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
7/8
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é LI em (Rn , R, +, · ).
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é LI em (C2 , R, +, · ).
(3) {(1, 0), (0, 1), (i, 0), (0, i)} é LD em (C2 , C, +, · ).
De fato: i · (1, 0) + 0 · (0, 1) − 1 · (i, 0) + 0 · (0, i) = (0, 0).
(4) O conjunto infinito
fn : [a, b] → R
t 7→ fn (t) = t n
n∈N
é um conjunto LI em C([a, b], R).
De fato: pelo teorema fundamental da álgebra,
(∀t ∈ [a, b], α1 · t n1 + · · · + αk · t nk = 0) ⇒ α1 = · · · = αk = 0.
36/62
Aula 1
Aplicações de Álgebra Linear
8/8
Bases
Definição
Sejam (V , K, +, · ) um espaço vetorial e B um subconjunto de V .
Dizemos que B é uma base de V se
(a) B for um conjunto gerador de V e
(b) B for linearmente independente.
37/62
Aula 1
Aplicações de Álgebra Linear
1/1
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é uma base do espaço
vetorial (Rn , R, +, · ). Ela é denominada base canônica de Rn .
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é uma base de (C2 , R, +, · ).
(3) {(1, 0), (0, 1)} é uma base de (C2 , C, +, · ).
(4) O conjunto infinito
fn : [a, b] → R
n
t 7→ fn (t) = t
n∈N∪{0}
é uma base de
P([a, b], R) = conjunto das funções polinomiais de [a, b] em R sobre K = R.
38/62
Aula 1
Aplicações de Álgebra Linear
1/4
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é uma base do espaço
vetorial (Rn , R, +, · ). Ela é denominada base canônica de Rn .
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é uma base de (C2 , R, +, · ).
(3) {(1, 0), (0, 1)} é uma base de (C2 , C, +, · ).
(4) O conjunto infinito
fn : [a, b] → R
n
t 7→ fn (t) = t
n∈N∪{0}
é uma base de
P([a, b], R) = conjunto das funções polinomiais de [a, b] em R sobre K = R.
38/62
Aula 1
Aplicações de Álgebra Linear
2/4
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é uma base do espaço
vetorial (Rn , R, +, · ). Ela é denominada base canônica de Rn .
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é uma base de (C2 , R, +, · ).
(3) {(1, 0), (0, 1)} é uma base de (C2 , C, +, · ).
(4) O conjunto infinito
fn : [a, b] → R
n
t 7→ fn (t) = t
n∈N∪{0}
é uma base de
P([a, b], R) = conjunto das funções polinomiais de [a, b] em R sobre K = R.
38/62
Aula 1
Aplicações de Álgebra Linear
3/4
Exemplos
(1) {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)} é uma base do espaço
vetorial (Rn , R, +, · ). Ela é denominada base canônica de Rn .
(2) {(1, 0), (0, 1), (i, 0), (0, i)} é uma base de (C2 , R, +, · ).
(3) {(1, 0), (0, 1)} é uma base de (C2 , C, +, · ).
(4) O conjunto infinito
fn : [a, b] → R
n
t 7→ fn (t) = t
n∈N∪{0}
é uma base de
P([a, b], R) = conjunto das funções polinomiais de [a, b] em R sobre K = R.
38/62
Aula 1
Aplicações de Álgebra Linear
4/4
Espaços Finitamente Gerados
39/62
Aula 1
Aplicações de Álgebra Linear
1/1
Espaços finitamente gerados
Definição
Dizemos que um espaço vetorial (V , K, +, · ) é finitamente gerado se
ele possui um conjunto gerador finito.
40/62
(1) (R2 , R, +, · )
é
(2) (R2 , Q, +, · )
não é
finitamente gerado.
(3) (Pn ([a, b], R), R, +, · )
não é
finitamente gerado.
(4) (Pn ([a, b], R), R, +, · )
é
Aula 1
finitamente gerado por B = {(1, 0), (0, 1)}.
finitamente gerado por B = {1, x, . . . , x n }.
Aplicações de Álgebra Linear
1/5
Espaços finitamente gerados
Definição
Dizemos que um espaço vetorial (V , K, +, · ) é finitamente gerado se
ele possui um conjunto gerador finito.
40/62
(1) (R2 , R, +, · )
é
(2) (R2 , Q, +, · )
não é
finitamente gerado.
(3) (Pn ([a, b], R), R, +, · )
não é
finitamente gerado.
(4) (Pn ([a, b], R), R, +, · )
é
Aula 1
finitamente gerado por B = {(1, 0), (0, 1)}.
finitamente gerado por B = {1, x, . . . , x n }.
Aplicações de Álgebra Linear
2/5
Espaços finitamente gerados
Definição
Dizemos que um espaço vetorial (V , K, +, · ) é finitamente gerado se
ele possui um conjunto gerador finito.
40/62
(1) (R2 , R, +, · )
é
(2) (R2 , Q, +, · )
não é
finitamente gerado.
(3) (Pn ([a, b], R), R, +, · )
não é
finitamente gerado.
(4) (Pn ([a, b], R), R, +, · )
é
Aula 1
finitamente gerado por B = {(1, 0), (0, 1)}.
finitamente gerado por B = {1, x, . . . , x n }.
Aplicações de Álgebra Linear
3/5
Espaços finitamente gerados
Definição
Dizemos que um espaço vetorial (V , K, +, · ) é finitamente gerado se
ele possui um conjunto gerador finito.
40/62
(1) (R2 , R, +, · )
é
(2) (R2 , Q, +, · )
não é
finitamente gerado.
(3) (Pn ([a, b], R), R, +, · )
não é
finitamente gerado.
(4) (Pn ([a, b], R), R, +, · )
é
Aula 1
finitamente gerado por B = {(1, 0), (0, 1)}.
finitamente gerado por B = {1, x, . . . , x n }.
Aplicações de Álgebra Linear
4/5
Espaços finitamente gerados
Definição
Dizemos que um espaço vetorial (V , K, +, · ) é finitamente gerado se
ele possui um conjunto gerador finito.
40/62
(1) (R2 , R, +, · )
é
(2) (R2 , Q, +, · )
não é
finitamente gerado.
(3) (Pn ([a, b], R), R, +, · )
não é
finitamente gerado.
(4) (Pn ([a, b], R), R, +, · )
é
Aula 1
finitamente gerado por B = {(1, 0), (0, 1)}.
finitamente gerado por B = {1, x, . . . , x n }.
Aplicações de Álgebra Linear
5/5
Proposição
Proposição
Se B = {v1 , . . . , vk } é um conjunto gerador de V , então todo conjunto
LI de V possui no máximo k elementos.
Demonstração.
Passo 1. Vamos mostrar que todo subconjunto de V com mais do que k
vetores é LD.
Passo 2. Seja X = {u1 , . . . , um } um subconjunto de V com m > k
elementos.
Passo 3. Como B = {v1 , . . . , vk } é um conjunto gerador para V , existem
escalares aij , com 1 ≤ i ≤ k e 1 ≤ j ≤ m tais que


 u1 = a11 · v1 + · · · + ak 1 · vk
..
.


um = a1m · v1 + · · · + akm · vk
41/62
Aula 1
=
Pk
· vi ,
=
Pk
· vi .
i=1 ai1
i=1 aim
Aplicações de Álgebra Linear
1/6
Proposição
Proposição
Se B = {v1 , . . . , vk } é um conjunto gerador de V , então todo conjunto
LI de V possui no máximo k elementos.
Demonstração.
Passo 1. Vamos mostrar que todo subconjunto de V com mais do que k
vetores é LD.
Passo 2. Seja X = {u1 , . . . , um } um subconjunto de V com m > k
elementos.
Passo 3. Como B = {v1 , . . . , vk } é um conjunto gerador para V , existem
escalares aij , com 1 ≤ i ≤ k e 1 ≤ j ≤ m tais que


 u1 = a11 · v1 + · · · + ak 1 · vk
..
.


um = a1m · v1 + · · · + akm · vk
41/62
Aula 1
=
Pk
· vi ,
=
Pk
· vi .
i=1 ai1
i=1 aim
Aplicações de Álgebra Linear
2/6
Proposição
Proposição
Se B = {v1 , . . . , vk } é um conjunto gerador de V , então todo conjunto
LI de V possui no máximo k elementos.
Demonstração.
Passo 1. Vamos mostrar que todo subconjunto de V com mais do que k
vetores é LD.
Passo 2. Seja X = {u1 , . . . , um } um subconjunto de V com m > k
elementos.
Passo 3. Como B = {v1 , . . . , vk } é um conjunto gerador para V , existem
escalares aij , com 1 ≤ i ≤ k e 1 ≤ j ≤ m tais que


 u1 = a11 · v1 + · · · + ak 1 · vk
..
.


um = a1m · v1 + · · · + ak m · vk
41/62
Aula 1
=
Pk
· vi ,
=
Pk
· vi .
i=1 ai1
i=1 aim
Aplicações de Álgebra Linear
3/6
Proposição
Proposição
Se B = {v1 , . . . , vk } é um conjunto gerador de V , então todo conjunto
LI de V possui no máximo k elementos.
Demonstração.
Passo 1. Vamos mostrar que todo subconjunto de V com mais do que k
vetores é LD.
Passo 2. Seja X = {u1 , . . . , um } um subconjunto de V com m > k
elementos.
Passo 3. Como B = {v1 , . . . , vk } é um conjunto gerador para V , existem
escalares aij , com 1 ≤ i ≤ k e 1 ≤ j ≤ m tais que


 u1 = a11 · v1 + · · · + ak 1 · vk
..
.


um = a1m · v1 + · · · + ak m · vk
41/62
Aula 1
=
Pk
· vi ,
=
Pk
· vi .
i=1 ai1
i=1 aim
Aplicações de Álgebra Linear
4/6
Proposição
Proposição
Se B = {v1 , . . . , vk } é um conjunto gerador de V , então todo conjunto
LI de V possui no máximo k elementos.
Demonstração.
Passo 1. Vamos mostrar que todo subconjunto de V com mais do que k
vetores é LD.
Passo 2. Seja X = {u1 , . . . , um } um subconjunto de V com m > k
elementos.
Passo 3. Como B = {v1 , . . . , vk } é um conjunto gerador para V , existem
escalares aij , com 1 ≤ i ≤ k e 1 ≤ j ≤ m tais que


 u1 = a11 · v1 + · · · + ak 1 · vk
..
.


um = a1m · v1 + · · · + ak m · vk
41/62
Aula 1
=
Pk
· vi ,
=
Pk
· vi .
i=1 ai1
i=1 aim
Aplicações de Álgebra Linear
5/6
Proposição
Proposição
Se B = {v1 , . . . , vk } é um conjunto gerador de V , então todo conjunto
LI de V possui no máximo k elementos.
Demonstração.
Passo 1. Vamos mostrar que todo subconjunto de V com mais do que k
vetores é LD.
Passo 2. Seja X = {u1 , . . . , um } um subconjunto de V com m > k
elementos.
Passo 3. Como B = {v1 , . . . , vk } é um conjunto gerador para V , existem
escalares aij , com 1 ≤ i ≤ k e 1 ≤ j ≤ m tais que


 u1 = a11 · v1 + · · · + ak 1 · vk
..
.


um = a1m · v1 + · · · + akm · vk
41/62
Aula 1
=
Pk
· vi ,
=
Pk
· vi .
i=1 ai1
i=1 aim
Aplicações de Álgebra Linear
6/6
Demonstração
Passo 4. Vamos agora estudar as combinações lineares de u1 , . . . , um em
termos de v1 , . . . , vk :
=
x1 · u1 + · · · + xm · um
=
x1 · (a11 · v1 + · · · + ak 1 · vk ) + · · · + xm · (a1m · v1 + · · · + ak m · vk )
(a11 · x1 + · · · + a1m · xm ) · v1 + · · · + (ak 1 · x1 + · · · + akm · xm ) · vk .
Passo 5. Para mostrar que {u1 , . . . , um } é LD, precisamos exibir x1 , . . . , xm
não todos nulos tais que a combinação linear acima resulta no
vetor nulo.
Passo 6. Para isto, basta exibir x1 , . . . , xm não todos nulos tais que


 a11 · x1 + · · · + a1m · xm = 0,
..
.


ak 1 · x1 + · · · + akm · xm = 0.
42/62
Aula 1
Aplicações de Álgebra Linear
1/5
Demonstração
Passo 4. Vamos agora estudar as combinações lineares de u1 , . . . , um em
termos de v1 , . . . , vk :
=
x1 · u1 + · · · + xm · um
=
x1 · (a11 · v1 + · · · + ak 1 · vk ) + · · · + xm · (a1m · v1 + · · · + ak m · vk )
(a11 · x1 + · · · + a1m · xm ) · v1 + · · · + (ak 1 · x1 + · · · + akm · xm ) · vk .
Passo 5. Para mostrar que {u1 , . . . , um } é LD, precisamos exibir x1 , . . . , xm
não todos nulos tais que a combinação linear acima resulta no
vetor nulo.
Passo 6. Para isto, basta exibir x1 , . . . , xm não todos nulos tais que


 a11 · x1 + · · · + a1m · xm = 0,
..
.


ak 1 · x1 + · · · + akm · xm = 0.
42/62
Aula 1
Aplicações de Álgebra Linear
2/5
Demonstração
Passo 4. Vamos agora estudar as combinações lineares de u1 , . . . , um em
termos de v1 , . . . , vk :
=
x1 · u1 + · · · + xm · um
=
x1 · (a11 · v1 + · · · + ak 1 · vk ) + · · · + xm · (a1m · v1 + · · · + ak m · vk )
(a11 · x1 + · · · + a1m · xm ) · v1 + · · · + (ak 1 · x1 + · · · + akm · xm ) · vk .
Passo 5. Para mostrar que {u1 , . . . , um } é LD, precisamos exibir x1 , . . . , xm
não todos nulos tais que a combinação linear acima resulta no
vetor nulo.
Passo 6. Para isto, basta exibir x1 , . . . , xm não todos nulos tais que


 a11 · x1 + · · · + a1m · xm = 0,
..
.


ak 1 · x1 + · · · + akm · xm = 0.
42/62
Aula 1
Aplicações de Álgebra Linear
3/5
Demonstração
Passo 4. Vamos agora estudar as combinações lineares de u1 , . . . , um em
termos de v1 , . . . , vk :
=
x1 · u1 + · · · + xm · um
=
x1 · (a11 · v1 + · · · + ak 1 · vk ) + · · · + xm · (a1m · v1 + · · · + ak m · vk )
(a11 · x1 + · · · + a1m · xm ) · v1 + · · · + (ak 1 · x1 + · · · + akm · xm ) · vk .
Passo 5. Para mostrar que {u1 , . . . , um } é LD, precisamos exibir x1 , . . . , xm
não todos nulos tais que a combinação linear acima resulta no
vetor nulo.
Passo 6. Para isto, basta exibir x1 , . . . , xm não todos nulos tais que


 a11 · x1 + · · · + a1m · xm = 0,
..
.


ak 1 · x1 + · · · + ak m · xm = 0.
42/62
Aula 1
Aplicações de Álgebra Linear
4/5
Demonstração
Passo 4. Vamos agora estudar as combinações lineares de u1 , . . . , um em
termos de v1 , . . . , vk :
=
x1 · u1 + · · · + xm · um
=
x1 · (a11 · v1 + · · · + ak 1 · vk ) + · · · + xm · (a1m · v1 + · · · + ak m · vk )
(a11 · x1 + · · · + a1m · xm ) · v1 + · · · + (ak 1 · x1 + · · · + akm · xm ) · vk .
Passo 5. Para mostrar que {u1 , . . . , um } é LD, precisamos exibir x1 , . . . , xm
não todos nulos tais que a combinação linear acima resulta no
vetor nulo.
Passo 6. Para isto, basta exibir x1 , . . . , xm não todos nulos tais que


 a11 · x1 + · · · + a1m · xm = 0,
..
.


ak 1 · x1 + · · · + ak m · xm = 0.
42/62
Aula 1
Aplicações de Álgebra Linear
5/5
Demonstração
Passo 6. Ou seja, o sistema linear homogêneo abaixo deve ter pelo menos
uma solução (x1 , . . . , xm ) não nula:


 a11 · x1 + · · · + a1m · xm = 0,
..
.


ak 1 · x1 + · · · + ak m · xm = 0.
Passo 7. Mas isto acontece, porque o número de equações (k ) é menor do
que o número de variáveis (m).
43/62
Aula 1
Aplicações de Álgebra Linear
1/2
Demonstração
Passo 6. Ou seja, o sistema linear homogêneo abaixo deve ter pelo menos
uma solução (x1 , . . . , xm ) não nula:


 a11 · x1 + · · · + a1m · xm = 0,
..
.


ak 1 · x1 + · · · + ak m · xm = 0.
Passo 7. Mas isto acontece, porque o número de equações (k ) é menor do
que o número de variáveis (m).
43/62
Aula 1
Aplicações de Álgebra Linear
2/2
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
1/8
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
2/8
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
3/8
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
4/8
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
5/8
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
6/8
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
7/8
Corolário
Corolário
Se (V , K, +, · ) é um espaço vetorial não nulo finitamente gerado,
então toda base de V possui o mesmo número de elementos,
denominado dimensão de V .
Demonstração. Sejam B e B 0 duas bases de V .
Passo 1. Como V é finitamente gerado e B e B 0 são LI, pela proposição
anterior, B e B 0 são conjuntos finitos.
Passo 2. Sejam então m = #B e m0 = #B 0 .
Passo 3. Como [B] = V e B 0 é LI, pela proposição anterior, m0 ≤ m.
Passo 4. Como [B 0 ] = V e B é LI, pela proposição anterior, m ≤ m0 .
Passo 5. Logo, m = m0 .
44/62
Aula 1
Aplicações de Álgebra Linear
8/8
Exemplos
(1) dimR (Rn ) =
(2) dimR (C2 ) =
(3) dimC (C2 ) =
(4) dimR (P([a, b], R)) =
(5) dimR (Mm×n (R)) =
(6) dimK ({0}) =
45/62
Aula 1
Aplicações de Álgebra Linear
1/8
Exemplos
(1) dimR (Rn ) = n.
(2) dimR (C2 ) =
(3) dimC (C2 ) =
(4) dimR (P([a, b], R)) =
(5) dimR (Mm×n (R)) =
(6) dimK ({0}) =
45/62
Aula 1
Aplicações de Álgebra Linear
2/8
Exemplos
(1) dimR (Rn ) = n.
(2) dimR (C2 ) = 4.
(3) dimC (C2 ) =
(4) dimR (P([a, b], R)) =
(5) dimR (Mm×n (R)) =
(6) dimK ({0}) =
45/62
Aula 1
Aplicações de Álgebra Linear
3/8
Exemplos
(1) dimR (Rn ) = n.
(2) dimR (C2 ) = 4.
(3) dimC (C2 ) = 2.
(4) dimR (P([a, b], R)) =
(5) dimR (Mm×n (R)) =
(6) dimK ({0}) =
45/62
Aula 1
Aplicações de Álgebra Linear
4/8
Exemplos
(1) dimR (Rn ) = n.
(2) dimR (C2 ) = 4.
(3) dimC (C2 ) = 2.
(4) dimR (P([a, b], R)) = ∞.
(5) dimR (Mm×n (R)) =
(6) dimK ({0}) =
45/62
Aula 1
Aplicações de Álgebra Linear
5/8
Exemplos
(1) dimR (Rn ) = n.
(2) dimR (C2 ) = 4.
(3) dimC (C2 ) = 2.
(4) dimR (P([a, b], R)) = ∞.
(5) dimR (Mm×n (R)) = m · n.
(6) dimK ({0}) =
45/62
Aula 1
Aplicações de Álgebra Linear
6/8
Exemplos
(1) dimR (Rn ) = n.
(2) dimR (C2 ) = 4.
(3) dimC (C2 ) = 2.
(4) dimR (P([a, b], R)) = ∞.
(5) dimR (Mm×n (R)) = m · n.
(6) dimK ({0}) = 0.
45/62
Aula 1
Aplicações de Álgebra Linear
7/8
Exemplos
(1) dimR (Rn ) = n.
(2) dimR (C2 ) = 4.
(3) dimC (C2 ) = 2.
(4) dimR (P([a, b], R)) = ∞.
(5) dimR (Mm×n (R)) = m · n.
(6) dimK ({0}) = 0. Lembre-se que, por convenção, ∅ é LI e [∅] = {0}.
45/62
Aula 1
Aplicações de Álgebra Linear
8/8
Corolário
Corolário
Seja (V , K, +, · ) um espaço vetorial de dimensão n ≥ 1.
(1) Todo conjunto de vetores com mais do que n elementos é LD.
(2) Nenhum conjunto com menos do que n elementos pode gerar V .
46/62
Aula 1
Aplicações de Álgebra Linear
1/1
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
α1
αk
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
1/8
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
αk
α1
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
2/8
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
α1
αk
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
3/8
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
α1
αk
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
4/8
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
α1
αk
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
5/8
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
α1
αk
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
6/8
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
α1
αk
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
7/8
Proposição
Proposição
Seja B = {v1 , . . . , vk } um subconjunto LI de um espaço vetorial V .
Se v 6∈ [B], então {v1 , . . . , vk , v} também é LI.
Demonstração.
Passo 1. Suponha, por absurdo, que {v1 , . . . , vk , v} seja LD.
Passo 2. Então existem escalares α1 , . . . , αk , α não todos nulos tais que
α1 · v1 + · · · + αk · vk + α · v = 0.
Passo 3. Obrigatoriamente, α 6= 0 pois, caso contrário, {v1 , . . . , vk } seria
LD.
Passo 4. Então, v = −
47/62
Aula 1
α1
αk
· v1 − · · · −
· vk ∈ [B]. Uma contradição.
α
α
Aplicações de Álgebra Linear
8/8
Teorema
Teorema
(1) Todo espaço vetorial não nulo finitamente gerado possui uma
base.
(2) Se B é subconjunto LI de um espaço vetorial V finitamente
gerado, então existe base de V que contém B.
48/62
Aula 1
Aplicações de Álgebra Linear
1/2
Teorema
Teorema
(1) Todo espaço vetorial não nulo finitamente gerado possui uma
base.
(2) Se B é subconjunto LI de um espaço vetorial V finitamente
gerado, então existe base de V que contém B.
48/62
Aula 1
Aplicações de Álgebra Linear
2/2
Proposição
Teorema
Seja V um espaço vetorial e sejam W1 , W2 dois subespaços vetoriais
de V , ambos de dimensão finita. Então
dimK (W1 + W2 ) = dimK (W1 ) + dimK (W2 ) − dimK (W1 ∩ W2 ).
49/62
Aula 1
Aplicações de Álgebra Linear
1/1
Coordenadas
50/62
Aula 1
Aplicações de Álgebra Linear
1/1
Proposição
Proposição
Seja V um espaço vetorial de dimensão n ≥ 1 e seja B ⊆ V . As duas
afirmações abaixo são equivalentes.
(a) B é uma base de V .
(b) Todo elemento de V se escreve de maneira única como
combinação linear de elementos de B.
51/62
Aula 1
Aplicações de Álgebra Linear
1/2
Proposição
Proposição
Seja V um espaço vetorial de dimensão n ≥ 1 e seja B ⊆ V . As duas
afirmações abaixo são equivalentes.
(a) B é uma base de V .
(b) Todo elemento de V se escreve de maneira única como
combinação linear de elementos de B.
51/62
Aula 1
Aplicações de Álgebra Linear
2/2
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
1/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
2/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
3/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
4/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
5/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
6/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
7/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
8/9
Demonstração: (a) ⇒ (b)
Como B é base de V , certamente B gera V . Logo, todo vetor v de V se
escreve como combinação linear de elementos de B. Resta mostrar que os
coeficientes desta combinação linear são únicos.
Passo 1. Vamos escrever B = {v1 , . . . , vn } e supor que
v = α1 · v1 + · · · + αn · vn = β1 · v1 + · · · + βn · vn .
Passo 2. Logo, (α1 − β1 ) · v1 + · · · + (αn − βn ) · vn = 0.
Passo 3. Como {v1 , . . . , vn } é LI, segue-se que α1 = β1 , . . . , αn = βn .
52/62
Aula 1
Aplicações de Álgebra Linear
9/9
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
1/8
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
2/8
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
3/8
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
4/8
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
5/8
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
6/8
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
7/8
Demonstração: (b) ⇒ (a)
Como, por hipótese, todo elemento v se escreve de maneira única como
combinação linear de elementos de B, segue-se que B gera V . Resta mostrar
que B é LI.
Passo 1. Seja v1 , . . . , vk ∈ V e α1 , . . . , αk ∈ K tais que
α1 · v1 + · · · + αk · vk = 0.
Passo 2. Temos também que:
0 · v1 + · · · + 0 · vk = 0.
Passo 3. Como, por hipótese, todo vetor se escreve de maneira única como
combinação linear de elementos de B, segue-se que
α1 = · · · = αk = 0.
Passo 4. Isto mostra que B é LI.
53/62
Aula 1
Aplicações de Álgebra Linear
8/8
Bases
Definição
Seja B = {v1 , . . . , vn } uma base de V . Fixando-se a ordem dos
elementos desta base, pela proposição anterior, cada elemento v
de V fica determinado de maneira unívoca pelos coeficientes
α1 , . . . , αn da combinação linear
v = α1 · v1 + · · · + αn · vn .
A n-upla ordenada
[v]B = (α1 , . . . , αn )B
será denominada coordenadas do vetor v com relação à base B.
54/62
Aula 1
Aplicações de Álgebra Linear
1/1
Aplicação
55/62
Aula 1
Aplicações de Álgebra Linear
1/1
Aplicação
Seja W o conjunto das soluções da equação diferencial linear
homogênea de ordem k com coeficientes constantes:
d k −1 f
dkf
df
+ ak −1 · k −1 + · · · + a1 ·
+ a0 f = 0.
k
dx
dx
dx
Isto significa que:
(1) f ∈ F(R, R),
(2) f tem derivada até ordem k para qualquer x ∈ R e
(3) ∀x ∈ R,
d k −1 f
df
dkf
(x)
(x) + · · · + a1 ·
+
a
·
(x) + a0 f (x) = 0.
k
−1
dx
dx k
dx k −1
Exercício: W é um subespaço de F(R, R).
Exercício mais interessante: W é um subespaço de C ∞ (R, R).
56/62
Aula 1
Aplicações de Álgebra Linear
1/4
Aplicação
Seja W o conjunto das soluções da equação diferencial linear
homogênea de ordem k com coeficientes constantes:
d k −1 f
dkf
df
+ ak −1 · k −1 + · · · + a1 ·
+ a0 f = 0.
k
dx
dx
dx
Isto significa que:
(1) f ∈ F(R, R),
(2) f tem derivada até ordem k para qualquer x ∈ R e
(3) ∀x ∈ R,
d k −1 f
df
dkf
(x)
(x) + · · · + a1 ·
+
a
·
(x) + a0 f (x) = 0.
k
−1
dx
dx k
dx k −1
Exercício: W é um subespaço de F(R, R).
Exercício mais interessante: W é um subespaço de C ∞ (R, R).
56/62
Aula 1
Aplicações de Álgebra Linear
2/4
Aplicação
Seja W o conjunto das soluções da equação diferencial linear
homogênea de ordem k com coeficientes constantes:
d k −1 f
dkf
df
+ ak −1 · k −1 + · · · + a1 ·
+ a0 f = 0.
k
dx
dx
dx
Isto significa que:
(1) f ∈ F(R, R),
(2) f tem derivada até ordem k para qualquer x ∈ R e
(3) ∀x ∈ R,
d k −1 f
df
dkf
(x)
(x) + · · · + a1 ·
+
a
·
(x) + a0 f (x) = 0.
k
−1
dx
dx k
dx k −1
Exercício: W é um subespaço de F(R, R).
Exercício mais interessante: W é um subespaço de C ∞ (R, R).
56/62
Aula 1
Aplicações de Álgebra Linear
3/4
Aplicação
Seja W o conjunto das soluções da equação diferencial linear
homogênea de ordem k com coeficientes constantes:
d k −1 f
dkf
df
+ ak −1 · k −1 + · · · + a1 ·
+ a0 f = 0.
k
dx
dx
dx
Isto significa que:
(1) f ∈ F(R, R),
(2) f tem derivada até ordem k para qualquer x ∈ R e
(3) ∀x ∈ R,
d k −1 f
df
dkf
(x)
(x) + · · · + a1 ·
+
a
·
(x) + a0 f (x) = 0.
k
−1
dx
dx k
dx k −1
Exercício: W é um subespaço de F(R, R).
Exercício mais interessante: W é um subespaço de C ∞ (R, R).
56/62
Aula 1
Aplicações de Álgebra Linear
4/4
Aplicação
Seja W o conjunto das soluções da equação diferencial linear
homogênea de ordem k com coeficientes constantes:
y (k ) + ak −1 y (k −1) + · · · + a1 y 0 + a0 y = 0.
Isto significa que:
(1) y ∈ F(R, R),
(2) y tem derivada até ordem k para qualquer x ∈ R e
(3) ∀x ∈ R,
y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0.
Exercício: W é um subespaço de F(R, R).
Exercício mais interessante: W é um subespaço de C ∞ (R, R).
57/62
Aula 1
Aplicações de Álgebra Linear
1/1
Teorema de Existência e Unicidade (TEU)
Teorema
Existe uma única solução y : R → R para o problema de valor inicial

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = c ,
0
58/62
Aula 1
y 0 (0) = c1 ,
...,
y (k −1) (0) = ck −1 .
Aplicações de Álgebra Linear
1/1
Teorema
Teorema
O subespaço W das soluções da equação diferencial linear
homogênea de ordem k com coeficientes constantes
y (k ) + ak −1 y (k −1) + · · · + a1 y 0 + a0 y = 0.
tem dimensão k .
59/62
Aula 1
Aplicações de Álgebra Linear
1/1
Demonstração
Seja y1 solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 1 ,
Seja y2 solução de
y 0 (0) = 0 ,
...,
y (k −1) (0) = 0 .

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 1 ,
...,
y (k −1) (0) = 0 .
..
.
Seja yk solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 0 ,
...,
y (k −1) (0) = 1 .
Fato: B = {y1 , . . . , yk } é base de W !
60/62
Aula 1
Aplicações de Álgebra Linear
1/5
Demonstração
Seja y1 solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 1 ,
Seja y2 solução de
y 0 (0) = 0 ,
...,
y (k −1) (0) = 0 .

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 1 ,
...,
y (k −1) (0) = 0 .
..
.
Seja yk solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 0 ,
...,
y (k −1) (0) = 1 .
Fato: B = {y1 , . . . , yk } é base de W !
60/62
Aula 1
Aplicações de Álgebra Linear
2/5
Demonstração
Seja y1 solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 1 ,
Seja y2 solução de
y 0 (0) = 0 ,
...,
y (k −1) (0) = 0 .

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 1 ,
...,
y (k −1) (0) = 0 .
..
.
Seja yk solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 0 ,
...,
y (k −1) (0) = 1 .
Fato: B = {y1 , . . . , yk } é base de W !
60/62
Aula 1
Aplicações de Álgebra Linear
3/5
Demonstração
Seja y1 solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 1 ,
Seja y2 solução de
y 0 (0) = 0 ,
...,
y (k −1) (0) = 0 .

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 1 ,
...,
y (k −1) (0) = 0 .
..
.
Seja yk solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 0 ,
...,
y (k −1) (0) = 1 .
Fato: B = {y1 , . . . , yk } é base de W !
60/62
Aula 1
Aplicações de Álgebra Linear
4/5
Demonstração
Seja y1 solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 1 ,
Seja y2 solução de
y 0 (0) = 0 ,
...,
y (k −1) (0) = 0 .

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 1 ,
...,
y (k −1) (0) = 0 .
..
.
Seja yk solução de

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = 0 ,
y 0 (0) = 0 ,
...,
y (k −1) (0) = 1 .
Fato: B = {y1 , . . . , yk } é base de W !
60/62
Aula 1
Aplicações de Álgebra Linear
5/5
Demonstração: B = {y1 , y2 , . . . , yk } gera V
Seja z ∈ W . Afirmamos que z = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
Passo 1. Note que f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk também satisfaz
o problema de valor inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 2. Note que a própria função z satisfaz o mesmo problema de valor
inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 3. Pelo Teorema de Existência e Unicidade, segue-se que
z = f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
61/62
Aula 1
Aplicações de Álgebra Linear
1/5
Demonstração: B = {y1 , y2 , . . . , yk } gera V
Seja z ∈ W . Afirmamos que z = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
Passo 1. Note que f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk também satisfaz
o problema de valor inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 2. Note que a própria função z satisfaz o mesmo problema de valor
inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 3. Pelo Teorema de Existência e Unicidade, segue-se que
z = f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
61/62
Aula 1
Aplicações de Álgebra Linear
2/5
Demonstração: B = {y1 , y2 , . . . , yk } gera V
Seja z ∈ W . Afirmamos que z = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
Passo 1. Note que f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk também satisfaz
o problema de valor inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 2. Note que a própria função z satisfaz o mesmo problema de valor
inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 3. Pelo Teorema de Existência e Unicidade, segue-se que
z = f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
61/62
Aula 1
Aplicações de Álgebra Linear
3/5
Demonstração: B = {y1 , y2 , . . . , yk } gera V
Seja z ∈ W . Afirmamos que z = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
Passo 1. Note que f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk também satisfaz
o problema de valor inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 2. Note que a própria função z satisfaz o mesmo problema de valor
inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 3. Pelo Teorema de Existência e Unicidade, segue-se que
z = f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
61/62
Aula 1
Aplicações de Álgebra Linear
4/5
Demonstração: B = {y1 , y2 , . . . , yk } gera V
Seja z ∈ W . Afirmamos que z = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
Passo 1. Note que f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk também satisfaz
o problema de valor inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 2. Note que a própria função z satisfaz o mesmo problema de valor
inicial:

 y (k ) (x) + ak −1 y (k −1) (x) + · · · + a1 y 0 (x) + a0 y (x) = 0,
 y (0) = z(0),
y 0 (0) = z 0 (0),
...,
y (k −1) (0) = z (k −1) (0).
Passo 3. Pelo Teorema de Existência e Unicidade, segue-se que
z = f = z(0)y1 + z 0 (0)y2 + · · · + z (k −1) (0)yk .
61/62
Aula 1
Aplicações de Álgebra Linear
5/5
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
1/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
2/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
3/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
4/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
5/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
6/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
7/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
8/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
9/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
10/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
11/12
Demonstração: B = {y1 , y2 , . . . , yk } é LI
Sejam α1 , . . . , αk escalares tais que α1 y1 + α2 y2 + · · · αk yk = 0. Sendo assim,
α1 y10 + α2 y20 + · · · αk yk0 = 0,
α1 y100 + α2 y200 + · · · αk yk00 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
= 0.
Agora
α1 y1 + α2 y2 + · · · αk yk = 0 ⇒ α1 y1 (0) + α2 y2 (0) + · · · αk yk (0) = 0 ⇒ α1 = 0,
α1 y10 + α2 y20 + · · · αk yk0 = 0 ⇒ α1 y10 (0) + α2 y20 (0) + · · · αk yk0 (0) = 0 ⇒ α2 = 0,
...
(k −1)
α1 y1
(k −1)
+ α2 y2
(k −1)
+ · · · αk yk
(k −1)
= 0 ⇒ α1 y1
(k −1)
(0) + α2 y2
(k −1)
(0) + · · · αk yk
(0) = 0 ⇒ αk = 0.
Isto demonstra que B = {y1 , y2 , . . . , yk } é LI.
62/62
Aula 1
Aplicações de Álgebra Linear
12/12