Estudo do movimento de queda de um balão

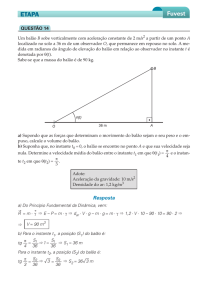
ACÇÃO DE FORMAÇÃO
ACTIVIDADES LABORATORIAIS PARA OS 10.º E 11.º ANOS DO ENSINO SECUNDÁRIO
Estudo do movimento de queda de um balão
Actividade Prática de Sala de Aula
Maria da Conceição da Mata Morais
Maria José Martins da Silva
Rosa Bela da Silva Correia Barros
Trabalho realizado na FCUP – Departamento de Física
21 de Julho de 2010
Actividade prática de sala de aula 11.º ano
Julho 2010
Sumário
Em corpos leves mas com volumes significativos, a resistência do ar tem um efeito não
desprezável.
Pode-se verificar esse efeito estudando o movimento de queda de um balão de borracha
recorrendo a um sensor de movimento ligado a um computador ou um CBR ligado a uma
calculadora gráfica.
É objectivo deste trabalho analisar o tipo de movimento adquirido por balões de massas
diferentes mas com o mesmo volume, assim como, determinar a velocidade terminal de cada
um.
Fundamento Teórico
A teoria de Galileu levou algum tempo a vingar, uma vez que a observação da queda de
objectos no dia-a-dia ocorre em condições naturais de atrito, e assim parece contrariá-la.
Repare-se no que acontece quando uma folha de papel aberta e lisa e uma folha de papel
amassado caem da mesma altura. Verifica-se que a folha de papel aberta demora mais tempo
a atingir o solo do que a de papel amassado.
Galileu explicou este fenómeno atribuindo-o ao facto de em determinadas circunstâncias não
se poder desprezar a resistência do ar. Quando um corpo cai no ar, sofre a acção de uma força
contrária ao sentido do seu movimento, que resulta da colisão e fricção com as moléculas do
ar. Este fenómeno faz com que a resultante das forças que actuam no corpo seja menor do que
seria se a resistência do ar pudesse desprezar-se.
A força de resistência do ar depende essencialmente de dois factores: da forma do corpo e da
velocidade. Quanto maior a velocidade do corpo maior a força de resistência do ar.
Considere-se o movimento de queda de um corpo com efeito da resistência do ar apreciável.
Inicialmente, o corpo está sujeito, apenas, à acção da força gravítica que a Terra exerce sobre
Pág. 2 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
ele. Assim, o corpo desce em queda livre e o seu movimento é, inicialmente, rectilíneo
uniformemente acelerado.
Após um certo intervalo de tempo, o ar oferece resistência ao movimento do corpo. Como a
intensidade da força gravítica aplicada no corpo é superior à intensidade da força de
resistência do ar, a qual vai aumentando uma vez que aumenta a norma da velocidade, o corpo
move-se com uma aceleração variável e adquire movimento rectilíneo acelerado.
No entanto, a partir de um determinado instante a intensidade da força de resistência do ar
iguala a intensidade da força gravítica pelo que a resultante das forças é nula. O corpo continua
a mover-se em direcção ao solo, agora com movimento uniforme. Assim, sob o efeito da
resistência do ar, ao fim de um certo tempo, o corpo atinge uma velocidade que se mantém
constante e se designa por velocidade terminal.
Material utilizado

Balões de borracha

Sensor de movimento CBR

Máquina de calcular gráfica

Cabo para ligar a calculadora ao CBR

Balança

Limalha de ferro
Procedimento
1) Prendeu-se um CBR a um suporte adequado, a uma distância do solo de cerca de 2 m.
2) Depois de executado o programa RANGER da calculadora, colocou-se o balão a cerca de
0,5 m do CBR, como se ilustra na figura 1.
Pág. 3 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
Fig. 1 – Esquema da montagem utilizada.
3) Premiu-se TRIGGER no CBR e quando a luz verde ficou intermitente, deixou-se cair o
balão de modo que o seu movimento se executasse por baixo do CBR.
4) Colocaram-se diferentes massas de limalha de ferro dentro de outros balões,
encheram-se com ar de modo que todos tivessem o mesmo volume e pesaram-se.
Seguidamente, repetiram-se os procedimentos de 1) a 3).
5) Registaram-se os dados obtidos.
Resultados obtidos
Balão A
Massa = 2,25 g
Tempo (s)
Altura* (m)
Velocidade (m/s)
0,52
0,56
0,60
0,65
0,69
0,73
0,77
0,82
0,86
0,90
0,95
0,99
1,03
1,08
0,94
0,94
0,91
0,87
0,83
0,78
0,74
0,69
0,64
0,59
0,53
0,48
0,43
0,38
0,01
-0,43
-0,75
-0,91
-0,98
-1,05
-1,13
-1,16
-1,19
-1,21
-1,21
-1,21
-1,21
-1,21
*Altura– posição do balão em relação ao solo
Pág. 4 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
Balão B
Massa = 3,56 g
Tempo (s)
Altura (m)
Velocidade (m/s)
0,43
0,47
0,52
0,56
0,60
0,65
0,69
0,73
0,77
0,82
0,86
0,90
0,95
0,99
1,03
1,08
0,94
0,93
0,89
0,85
0,80
0,75
0,69
0,64
0,58
0,51
0,45
0,39
0,32
0,25
0,19
0,12
-0,18
-0,62
-0,94
-1,04
-1,13
-1,22
-1,31
-1,37
-1,44
-1,48
-1,50
-1,51
-1,52
-1,51
-1,51
-1,52
Tempo (s)
Altura (m)
Velocidade (m/s)
Balão C
Massa = 4,64 g
0,47
0,52
0,56
0,59
0,65
0,69
0,73
0,77
0,82
0,86
0,90
0,95
0,92
0,86
0,80
0,74
0,66
0,59
0,51
0,43
0,35
0,27
0,20
0,12
-0,80
-1,20
-1,41
-1,62
-1,70
-1,76
-1,80
-1,78
-1,81
-1,81
-1,80
-1,80
No final de cada ensaio analisaram-se os gráficos da posição e da velocidade em função do
tempo; seleccionou-se, para cada caso, a região que representa o intervalo de tempo desde o
início do movimento até o balão atingir o solo e transferiram-se os resultados para o programa
EXCEL do computador.
Pág. 5 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
Tratamento de resultados
A partir dos resultados obtidos, reproduziram-se, no programa EXCEL os gráficos da posição e
da velocidade em função do tempo, relativos ao intervalo de tempo que decorre entre o início
do movimento até o balão atingir o solo.
Balão A
Velocidade-Tempo
Posição-Tempo
0,8
velocidade/ms-1
posição/m
.
.
1,0
0,6
0,4
0,2
0,0
0,40
0,50
0,60
0,70
0,80
0,90
1,00
1,10
0,0
0,40
-0,2
0,50
0,60
0,70
0,80
0,90
1,00
1,10
1,20
1,00
1,10
1,20
-0,4
-0,6
-0,8
-1,0
-1,2
-1,4
1,20
tempo/s
tempo/s
Balão B
Posição-Tempo
Velocidade-Tempo
.
1,10
0,50
0,60
0,70
0,80
0,90
-0,4
0,70
velocidade/ms-1
Posição/m
.
0,90
0,0
-0,20,40
0,50
0,30
0,10
-0,100,40
0,50
0,60
0,70
0,80
0,90
1,00
1,10
-0,6
-0,8
-1,0
-1,2
-1,4
-1,6
1,20
tempo/s
tempo/s
Balão C
Posição-Tempo
Velocidade-Tempo
1,0
.
-1
0,6
velocidade/ms
.
posição/m
0,0
0,8
0,4
0,2
0,0
0,40
0,50
0,60
0,70
tempo/s
0,80
0,90
1,00
-0,20,40
-0,4
0,50
0,60
0,70
0,80
0,90
1,00
-0,6
-0,8
-1,0
-1,2
-1,4
-1,6
-1,8
-2,0
tempo/s
Pág. 6 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
A partir de determinado instante (0,86s para os balões A e B e 0,77s para o balão C) observase, sempre, que o gráfico posição-tempo toma a forma linear. Para os intervalos decorridos
desde esse instante até ao instante em que os balões tocam no solo, construíram-se os gráficos
de dispersão posição-tempo e determinaram-se as equações da recta que melhor se ajustam a
cada conjunto de pontos.
Os gráficos obtidos foram:
Balão A
Velocidade Terminal
posiçao/m .
0,7
0,6
y = -1,21x + 1,68
0,5
0,4
0,3
0,85
0,90
0,95
1,00
1,05
1,10
tempo/s
Balão B
Velocidade Terminal
Posição/m
.
0,5
y = -1,53x + 1,76
0,4
0,3
0,2
0,1
0,0
0,80
0,85
0,90
0,95
1,00
1,05
1,10
tempo/s
Balão C
Velocidade Terminal
posiçao/m
.
0,5
0,4
y = -1,81x + 1,83
0,3
0,2
0,1
0,0
0,75
0,80
0,85
0,90
0,95
1,00
tempo/s
Pág. 7 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
O declive da recta obtida fornece, para cada caso, o valor da velocidade terminal. Assim,
Velocidade terminal do balão A: vA = 1,21 ms-1
Velocidade terminal do balão B: vB = 1,53 ms-1
Velocidade terminal do balão A: vA = 1,81 ms-1
Conclusões e Crítica
A partir dos resultados obtidos observa-se que, qualquer que seja a massa do balão, este
adquire, a partir de determinado instante, velocidade constante – velocidade terminal. Esse
facto é traduzido pela linearidade dos gráficos posição em função do tempo e pela constância
do valor registado para as velocidades.
Os valores da velocidade determinados para os balões de massas de 2,25 g, 5,56 g e 4,64 g
foram, respectivamente, 1,21 ms-1, 1,53 ms-1 e 1,81 ms-1. Conclui-se assim que, quando
largados da mesma altura, quanto maior a massa do balão maior o valor da velocidade
terminal e menor a altura, em relação ao solo, para a qual essa velocidade é adquirida. O
tempo de queda é diferente para cada balão. Para o balão de maior massa o tempo de queda é
menor.
Quanto ao tipo de movimento adquirido pelos balões, observa-se que até ao instante em que
atingem a velocidade terminal, todos os balões adquiriram movimento acelerado mas não
uniformemente e, posteriormente ao instante referido, movimento uniforme. De facto, até
atingirem a velocidade terminal, registaram, para todos os balões, variações do valor da
velocidade que diminuíram de forma não linear.
Há ainda a salientar que, para balões de massa superior a 5,0 g quando largados de uma altura
de 1,5m, não se conseguiu fazer o registo da velocidade terminal, pois para tal, seria
necessário aumentar a altura de queda.
Pág. 8 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
Bibliografia
Caldeira, H., Bello, A., Ontem e Hoje 10/11, Porto, Porto Editora, 2007
Escoval, M. T., Capucho, R.T., Problemas de Física e Química, 1ª edição, Lisboa, Editorial
Presença, 2006
Rodrigues, M., Dias, F., Física na Nossa Vida 11, Porto, Porto Editora, 2008
Ventura., G., Fiolhais, C., 11 F – Física e Química A, 1ª Edição, Lisboa, Texto Editores, 2008
Pág. 9 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
Anexo
Pág. 10 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
APSA – Estudo do movimento de queda de um balão
Objectivo da actividade:
Estudar o efeito da força de resistência do ar na queda de um balão.
Material:
Balões de borracha
Limalha de ferro
CBR
Cabo de ligação da calculadora ao CBR
Máquina de calcular gráfica
Balança
Como proceder:

Identificar as variáveis a medir que permitem estudar o movimento de queda de um balão;

Efectuar a montagem indicada na figura 1;

Medir e registar a massa do balão;

Utilizar o CBR para estudar o movimento do balão;

Transferir os dados obtidos para a máquina de calcular e visualizar os gráficos da posição em função do
tempo e da velocidade em função do tempo.

Repetir a experiência utilizando dois balões com diferentes massas.
Fig. 1
Análise dos dados obtidos:
1. Para o gráfico posição-tempo seleccione a região que representa o intervalo de tempo desde o início do
movimento até o balão atingir o solo.
1.1. A partir de um dado instante, o gráfico passa a ter uma forma linear. Identifique o tipo de movimento do
balão a partir desse instante.
1.2. Seleccione a região do gráfico cuja forma é aproximadamente linear.
1.2.1. Para o intervalo de tempo seleccionado, construa o gráfico posição em função do tempo e determine a
equação da recta.
Pág. 11 de 12
Actividade prática de sala de aula 11.º ano
Julho 2010
1.2.2. Qual é o significado físico do declive da recta obtida?
1.3. Faça uma análise do gráfico da velocidade em função do tempo, obtido experimentalmente.
1.4. Calcule o valor para o qual a velocidade do balão é aproximadamente constante. Como se designa esta
velocidade?
1.5. Compare o valor calculado na alínea anterior como o obtido na alínea 1.2.2.
1.6. Identifique, num esquema, as forças que actuam no balão durante a queda, em dois instantes diferentes:
 antes da atingir a velocidade constante;
 após atingir a velocidade constante.
1.7. Da análise dos gráficos posição-tempo e velocidade-tempo, que conclusão pode tirar sobre o valor da
força de resistência do ar?
2.
Trace os gráficos posição-tempo e velocidade-tempo para os restantes balões. Analise os gráficos
obtidos, para os três ensaios, e tire conclusões.
Pág. 12 de 12