46 AULA 6 Expressões Algébricas São expressões

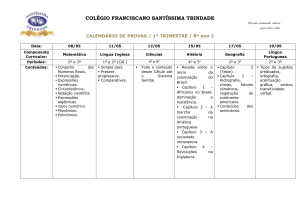
AULA 6
Forma reduzida e monômios semelhantes
Expressões Algébricas
Podemos escrever o monômio 6.a.(-3).x2 em
uma forma reduzida sendo dada por
-18ax2.
São expressões matemáticas que envolvem
números, letras e as operações indicadas
entre eles. As letras são as variáveis de uma
expressão algébrica e podem representar
qualquer número real.
Além disso, dois ou mais monômios são
chamados semelhantes quando têm partes
literais iguais.
Exemplo: 2a2b
semelhantes.
e
-5a2b
são
monômios
Exemplos:
a) 10ax + 4b
Operações entre monômios
2
b) ax + bx + c
c) 7a
Adição e Subtração entre monômios
Valor numérico
algébrica
A soma ou a diferença de dois monômios
semelhantes é um monômio com:
Coeficiente igual à soma algébrica dos
coeficientes;
Parte literal igual à desses monômios.
de
uma
expressão
É o resultado que obtemos quando
atribuímos às letras dessa expressão valores
numéricos e efetuamos as operações nela
indicadas.
Exemplo: A expressão 20t representa a
quantidade de parafusos produzidos em t
horas. Determine quanto parafusos são
produzidos em 4 horas.
Substituindo t por 4 na expressão 20t
obtemos a quantidade de parafusos
produzidos em 4 horas. Assim, 20t=20.4=80
parafusos.
Monômio
São expressões algébricas que representam
um produto de números reais por uma parte
literal formada por letras e seus expoentes,
que devem ser números naturais.
Exemplo:
Exemplos:
a) 3x2y3 + 5 x2y3 = (3 + 5) x2y3 = 8 x2y3
b) 39x5y4
25 x5y4
5 4
y =14x5y4
Multiplicação e Divisão entre monômios
Multiplicação entre monômios
A multiplicação entre dois ou mais monômios
é um monômio com:
Coeficiente igual ao produto dos
coeficientes desses monômios;
Parte literal igual ao produto das partes
literais desses monômios.
Exemplo:
(2ax2).(5a3xy) = (-2.5).a.a3.x2.x.y=
= -10.a1+3.x2+1.y =
= -10a4x3y
Divisão entre monômios
A divisão ou quociente entre dois monômios
com divisor diferente de zero, tem:
Coeficiente igual ao quociente entre os
coeficientes desses monômios;
46
Parte literal igual ao quociente entre as
partes literais desses monômios.
Exemplo:
Trinômio: é uma soma algébrica de três
monômios. Exemplo: ax2 + bx + c
Polinômio:
monômios.
é
uma
soma
Obs: Monômios também
chamados de polinômios.
Potência de um monômio
A potência de um monômio é um monômio
com:
Coeficiente
igual
à
potência
do
coeficiente desse monômio;
Parte literal igual à potência da parte
literal desse monômio.
Exemplo:
Simplificação de expressões algébricas
Podemos
simplificar
as
expressões
algébricas
que
envolvem
operações
procedendo da mesma forma que em
expressões numéricas. Efetuamos primeiro
às potências, em seguida calculamos os
produtos e o quocientes e, finalmente, as
somas algébricas, reduzindo os termos
semelhantes.
Exemplo: Simplifique a expressão algébrica
algébrica
de
podem
ser
Grau de um polinômio (não nulo) com uma
variável é o maior expoente da variável que
tem coeficiente diferente de zero.
Exemplo:O grau do polinômio 6t2 + 20t -3 é 2,
pois é o maior expoente de t com coeficiente
diferente de zero.
Operações entre polinômios
Adição e subtração de polinômios
Para somar ou subtrair polinômios,
colocamos termo semelhante abaixo de
termo semelhante e efetuamos a adição ou
subtração. Veja os exemplos a seguir:
a) (a + 4ab) + (9a - 6ab - 6) =
=10ª 2ab 6
a + 4ab
+ 9a 6ab 6
---------------------10a 2ab 6
b) (8x3 + 6x2 7)
= 8x3 - x2 2
(7x2
5) =
Para calcular a diferença, eliminamos os
parênteses trocando os sinais de 7x2 5. Em
seguida, efetuamos a adição entre os
polinômios.
8x3+ 6x2 7
+
- 7x2 + 5
é o oposto 7x2
---------------------8x3 - x2 2
5.
Multiplicação e divisão de polinômios
Binômios Trinômios e Polinômios
Binômio: é uma soma algébrica de dois
monômios. Exemplo: ax + b
Calculamos o produto de dois polinômios
multiplicando cada termo de um deles por
todos os termos do outro e reduzindo os
termos semelhantes.
Exemplo: Determine o produto:
47
Exemplo:
Para calcular o quociente e o resto da divisão
entre x4+ 4x3 + 4x2 + 9 por x2 + x
1,
escrevemos os polinômios na forma
completa e na ordem decrescente dos
expoentes dos monômios.
Inicialmente, dividimos o termo de maior grau
do dividendo pelo termo de maior grau do
divisor.
Dividimos um polinômio por um monômio,
não nulo, dividindo cada termo desse
polinômio por esse monômio.
Exemplo: Faça a divisão de 36x6
6x2.
(36x6
12x5)
12x5 por
Em seguida, calculamos x2 . (x2 + x 1) e
subtraímos o resultado do dividendo. ... ou
adicionamos o oposto a ele.
Faremos este processo, até que o resto da
divisão resulte em um polinômio cujo grau é
menor do que o grau do divisor. Assim:
6x2 =
Dividimos um polinômio por outro
polinômio, não nulo, de maneira semelhante
ao utilizado para os números.
Em geral, em uma divisão de polinômios
podemos escrever uma relação entre
multiplicação e divisão: quociente x divisor +
resto = dividendo.
Por exemplo: Na divisão de (6x3
1) por (x-2):
5x2
17x
EXERCÍCIOS
Aula 6
01) Escreva cada frase a seguir usando
uma expressão algébrica:
a) A soma do quadrado de um número x
com um número y.
b) O quociente entre o quadrado de um
número a e o quadrado de um
número b, diferente de zero, nessa
ordem.
c) O quadrado da diferença entre um
número x e um número y, nessa
ordem.
02) Determine o valor numérico da
expressão a2 + 2ª + 3 para a = - 5
Temos:
03) Qual é o valor numérico da expressão
algébrica:
para y = 4?
04) Determine o valor de x para o qual
não existe o valor numérico destas
expressões algébricas:
48
a)
;
b)
;
13) Efetue as operações e simplifique as
expressões algébricas:
c)
05) Para quais valores de x o valor
numérico da expressão
não é um número real?
a) x = 0; b) x = 4; c) x = 6,4 d) x = 10
Determine o valor numérico dessa
expressão algébrica quando ele for um
número real.
06) Os monômios
e
são
semelhantes? Justifique sua resposta.
07) Quando um monômio é nulo?
a) (3y2) - y2 + 3y2
b)
c)
14) Qual é o quadrado de
11ª2b3?
15) Calcule as potências:
a) (-3x2y3)3
b) (0,2y2z)5
c)
08) Calcule a soma e a diferença, na
ordem dada, entre estes monômios:
a) -5x2 e -7x2
b)
ay3 e 10ay3
c)
e
d)
e
e)
d)
0,3ay4)2
e)
1,2ª4b2)2
f)
16) Simplifique as expressões algébricas:
a)
b)
e
c)
09) Qual é o monômio que na forma
reduzida
corresponde
a:
17) Qual é o resultado de
?
10) Calcule estas somas algébricas:
?
18) Considere a expressão algébrica
(5y+4y)2 - (5y 4y)2 e responda:
a) Ela é um monômio? Qual?
b) Qual é o valor numérico da expressão
para y = -3?
a)
b)
11) Qual é o monômio que multiplicado
por 20x3y tem como produto -18x4y2?
12) Calcule os produtos:
a)
b)
c)
19) O valor numérico da expressão a3
3a2 . x2 . y2 , em que a = 10, x = 3 e y
= 1, é igual a: _____
20) Um polinômio que possui monômios
semelhantes pode ser escrito na
forma reduzida, ou seja, com um
número menor de termos. Em posse
dessa informação, determine a forma
reduzida dos polinômios:
a)
b)
49
21) Qual é o valor numérico do polinômio
y4 y2 + 1 para y = -1/2
22) Qual é o valor numérico do polinômio
para y = - 4
23) Calcule o valor de y para o qual o
valor numérico do polinômio 5y 7 é
13.
24) Para qual valor de a o valor numérico
do binômio
é igual a zero?
25) Quais são os valores de m e n para
que o polinômio (m 2)y3 + (2n 1)y2
seja nulo?
26) Obtenha a soma de (-25ª + 7ab) com
(-4ab + 16a)
27) Calcule (32a
18c 27b)
40b
18c)
(27a
2
28) Calcule A B, sendo A = -3m + 20m
+ 14 e B = 14 + 31m 10m2
29) Calcule a soma de
com
30) Que polinômio adicionado a 8a3 +
14a2 9 resulta em a3 + a2 2ª + 6 ?
31) A soma de dois polinômios é igual a
.
Um
deles
é
.
Qual
é
o
outro
polinômio?
32) Considere os polinômios A = x2
2xy+ 4y2 e B = -2x2 + 2xy + 4y2.
a) Qual é o resultado de (A B)?
b) Qual é o valor numérico de (A
B) para x = 1 e y = ¼ ?
c) Que expressão algébrica se
obtém para (A - B)?
d) Relacione o valor numérico de
(A B) para x = 1 e y = ¼ com o
valor de (A B) obtido no item b.
33) Que monômio deve ser adicionado a
7a4 4a2 12a + 19 para se obter um
trinômio do 2º grau?
34) Qual é o produto do monômio -13ab2
pelo polinômio (-2ª + 5b 3a2b 6)?
35) Considere P =
e
Q =
a) Qual é o produto de P por Q?
b) Qual é o valor numérico de P.q
para m = - 2 e n = 0?
36) Calcule o produto dos seguintes
polinômios:
a) (x + 3).(x + 3)
b) (5a + 1).(5a + 2)
c) (y + 4).(y2 + 3y)
d) (12x + 30).(x/6 + 1/3)
e) (x + 1/3).(9x + 15)
f)
(x + 2).(x2
2x + 4)
g) (12x2 + 6x
3).(2x
1)
h) (7y2 + 2y + 2).(10y2 + 4y
4)
37) Sabendo que P = 9a2 3ª, M = 3ª + 1
e R = 9a2 + 1, responda:
a) Qual é o polinômio P.M.R ?
b) Qual é o polinômio
?
38) Dados os polinômios A = x 1, B = x2
+ x e C = x, determine os polinômios:
a) A.B
b) B.C
c) A.a ou A2
d) A.B B.C + A.C
39) Calcule o produto dos polinômios e
reduza os termos semelhantes:
a) a.(2a + b + 2) + b.(- a b+ 12)
12.(a + b- 1)
b) (3x - 2).(2x + 3)
6x.(x + 1)
40) Se A = x.(3x 1) e B = (x + 5).(3x
determine os polinômios:
a) A B
b)
13.(A B)
2)
41) Que polinômio é o resultado da
divisão de 36x2 12x5 por 6x2?
50