Circuito Potenciómetro, Tensões de Referência e

Capítulo IV Potenciómetros; Tensões de Referência e Pontes
balanceadas dc e ac.
INDICE
4. APLICAÇÃO DE POTENCIOMETROS E TENSÕES DE REFERÊNCIA. PONTES.........................2
4.1 O potenciómetro..................................................................................................2
4.1.1 O Potenciómetro em circuitos de precisão ............................................................. 2
4.1.2 Potenciómetro de fita e suas aplicações ................................................................ 5
4.1.3 Potenciómetros rotativos .................................................................................... 6
4.1.4 Problemas. ....................................................................................................... 7
Problema 4.5....................................................................................................... 8
4.1.5 Aplicações ........................................................................................................ 9
4.2 TENSÕES DE REFERÊNCIA....................................................................................9
4.2.1 Nomenclatura Usual ........................................................................................ 11
4.2. Erro de saída e definições de precisão de uma referência ........................................ 12
Bibliografia ............................................................................................................. 13
4.2.1 Caixa de tensões ............................................................................................13
4.3 . PONTES DE CORRENTE CONTINUA ...................................................................13
4.3.1 Ponte de Wheatstone .....................................................................................13
4.3.2 PONTE DE KELVIN ........................................................................................... 16
4.3.3 Circuito de um quarto de ponte.......................................................................16
4.3.4 Aplicações de pontes na determinação de parâmetros distribuídos de cabos ............ 19
4.4. PONTES DE CORRENTE ALTERNA ......................................................................21
4.4.1 Diferentes tipos de pontes de corrente alterna ...............................................23
4.4.1.1 PONTE DE PEQUENOS ÂNGULOS..................................................................... 23
4.4.1.2 PONTE DE MAXWELL ..................................................................................... 24
4.4.1.3 PONTE DOS ÂNGULOS OPOSTOS OU DE HAY.................................................... 24
4.4.1.4 PONTE DE WIEN........................................................................................... 25
4.4.1.5 PONTES DE RÁDIO FREQUÊNCIA .................................................................... 25
4.4.1.6 PONTE DE SCHERING.................................................................................... 26
Sites a Consultar .....................................................................................................27
4. APLICAÇÃO DE POTENCIOMETROS E TENSÕES DE REFERÊNCIA. PONTES
4.1 O potenciómetro
É uma resistência eléctrica de elevada precisão, variável e com três terminais acessíveis. Os
extremos da resistência estão ligadas a duas entradas de tensão do circuito eléctrico e o
terceiro terminal, ligado à saída do circuito, é ajustável ao longo de um elemento da
resistência situado entre os dois terminais fixos, dividindo deste modo a resistência em duas
componentes.
Uma vez que a posição do terminal móvel determina qual a
percentagem da tensão de entrada que é aplicada ao circuito, o
potenciómetro pode ser utilizado para variar a tensão aplicada a
um circuito, pelo que é também conhecido como divisor de
tensão. Normalmente os potenciómetros são utilizados em : (1)
circuitos de calibração e de precisão de fontes de tensão; (2)
controlo do volume de rádios e de controlo de brilho das
Figura 4.1 Potenciómetro
televisões.
Figura 4.2 Esquemático de um potenciómetro, evidenciando a sua estrutura e terminais.
Para além do potenciómetro, existem outras formas
de
resistências
variáveis,
cujo
comportamento é similar ao do potenciómetro e quer são:
(1) “trimmer”, é uma resistência ajustável e que se utiliza muito em PCB. O ajuste é feito
normalmente rodando o seu cursor com uma pequena chave de fenda e normalmente não
é utilizada em sistemas que necessitem de um ajuste frequente.
(2) O reostato é uma resistência variável de 3 terminais, que normalmente só usa dois dos
seus terminais.
Os materiais utilizados na sua concepção são fio de cromo-niquel enrolado sobre um suporte
isolante do tipo cerâmico; carvão; polimero condutor ou mistura oxido -metal (cermet).
4.1.1 O Potenciómetro em circuitos de precisão
O efeito de carga em instrumentos de medida vai influenciar o valor final indicado pelo
aparelho de medida. Este efeito é mais crítico e portanto, o erro associado maior, quando o
IV/2
circuito eléctrico de medida é de baixa tensão ou se pretende uma grande precisão do valor
medido. Mesmo quando se utilizam instrumentos de uma elevada impedância de entrada para
se medir uma dada tensão, uma pequena porção do sinal de medida (corrente) é subtraída do
circuito em teste, dando origem a uma queda de tensão IR, associada ao erro de medida.
Uma forma de se eliminar o efeito de carga num processo de medida é o de se utilizar um
circuito balanceador que não provoque qualquer perturbação ao circuito sob teste. Para isso,
recorre-se a uma segunda fonte de tensão, externa ao circuito sob teste, capaz de gerar uma
corrente idêntica à do circuito teste, mas que flua em sentido contrário. Para a obtenção de tal
condição, é necessário recorrer-se a um circuito detector, capaz de indicar que, para a tensão
padrão escolhida, a corrente é igual e de sentido contrário à do circuito teste. Tal consegue-se
associando em série com a fonte de tensão uma resistência variável de alta precisão,
designada de potenciómetro, que para além de limitar a corrente (através de um reostato),
permite controlar o seu valor (potenciómetro, propriamente dito), através das queda de tensão
aos seus terminais (móveis), directamente proporcional ao comprimento da resistência do
potenciómetro.
Para a calibração do potenciómetro a primeira operação consiste em ajustar-se a corrente que
passa por este, através do reostato, de modo a que a queda de tensão aos seus terminais
(xy), seja proporcional ao seu comprimento. Depois liga-se os seus terminais a um circuito
padrão, constituído por uma tensão padrão (em oposição a V) e um galvanómetro (detector),
ligado a uma resistência de protecção. Quando se liga o galvanómetro ao circuito, o reostato
deve ser ajustado de modo que a indicação no galvanómetro seja nula. Uma vez conseguido
esse balanceamento, a resistência de protecção do galvanómetro deve ser cuto-circuitada, de
modo a aumentar a sua sensibilidade e reajustar o valor de leitura (nula) do galvanómetro.
Nestas condições, o galvanómetro encontra-se em condições de ser utilizado na medida de
forças electromotrizes (traduzidas em potenciais) desconhecidas.
S
V
R
(Reóstato)
Y
Saída do potenciómetro
X
G
Circuito de
calibração
Figura 4.3a) Circuito Potenciométrico de Calibração de fontes de tensão
Na figura que se segue mostra-se o caso de utilização de um potenciómetro utilizado num
processo de calibração prática onde se deve ter em conta que IRx = Ex e IRn = En.
Nestas condições tem-se que:
IV/3
Ex =
Rx
l
En = x En
Rn
ln
(4.1)
Figura 4.3b) Circuito Potenciométrico de Calibração de fontes de tensão
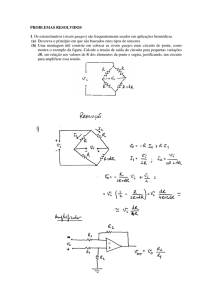
Problema 4.1- Considere a montagem que se mostra acima em que o fio de cromo-níquel
que constitui o potenciómetro tem um comprimento de 200 cm e uma resistência de
200 Ω, ligado a uma fonte de tensão de 3 V. Sabendo que o valor da tensão padrão utilizada
como referência é de 1,356 V, determine o valor da corrente de trabalho, a resistência do
reostato e a resolução do potenciómetro, quando utilizado para medir a força electromotriz de
uma fonte desconhecida em que o comprimento útil do potenciómetro é de 100 cm e o valor
da escala mínima de leitura 0,5 mm.
A
resistência
R100 =
correspondente
ao
comprimento
útil
do
potenciómetro
é
de
100cm × 200Ω
1,356
= 100Ω e a correspondente corrente de trabalho é I =
= 13,56 mA.
200cm
100
A queda de tensão correspondente no potenciómetro é de V P = IR = 13,56 × 10
V, pelo que a resistência do reostato é R =
−3
× 200 = 2,712
3V − 2,712
= 21,2 Ω .
13,56 × 10 −3
Para o cálculo da resolução devemos saber quantas divisões tem a escala. de acordo com o
enunciado tem-se:
Númerodedivisõesdaescala =
: resolução =
IV/4
200cm × 10mm / cm
= 4000 , pelo que a resolução da escala será de
0,5mm
2,712
= 0,68 mV.
4000
4.1.2 Potenciómetro de fita e suas aplicações
Anteriormente dissemos que o potenciómetro tem uma “fita resistiva linear”. Isto é, que a
resistência varia linearmente com o seu comprimento. Deste modo é possível calibrar-se o
comprimento da fita com um dado essencial onde o potenciómetro se insira, como seja o de
controlar uma fonte de tensão dc ou o volume de um rádio.
Figura 4.4 Potenciómetro como divisor de tensão.
No caso de divisor de tensão liga-se o terminal de referência da fonte (normalmente o
negativo) a um dos contactos fixos do potenciómetro e o outro terminal (terminal móvel) será
a saída, tal como se mostra no diagrama acima.
Figura 4.5 Formas de onda de saída ac e dc de um potenciómetro
Se o potenciómetro fosse ligado a um gerador ac (gerador de onda sinusoidal) o valor da
tensão de saída seria 63% da tensão de entrada. No gráfico que se segue mostramos os
diagramas das tensões de saída para os casos dc e ac.
Para o caso do potenciómetro ser utilizado para o controlo do volume de um rádio, precisamos
de utilizar um potenciómetro cuja fita resistiva varie de modo logaritmo, uma vez que o
IV/5
sistema
auditivo
humano
funciona
logaritmicamente.
Caso
utilizássemos
um
sistema
potenciométrico linear para controlar o volume de um rádio num dos seus extremos seria
irritável. Isto é, daria a sensação que o volume aumentava muito rapidamente no extremo do
botão.
No gráfico que se segue pode-se ver que o valor da resistência quando varia linearmente
(traçado a vermelho) a 50% do seu comprimento o seu valor é também de 50%, enquanto
que no traçado logarítmico (traçado a amarelo) a 50% do seu comprimento, o valor da
resistência é de cerca de 23% do seu valor. Para se obter 50% do valor da resistência, o
comprimento necessário da fita é de cerca de 85%.
Figura 4.6 Esquemático da variação da resistência em fita de um potenciómetro com o seu
comprimento para: uma variação linear (vermelho) e uma variação logarítmica (amarelo).
4.1.3 Potenciómetros rotativos
O diagrama que se segue mostra dois potenciómetros rotativos respectivamente a 50% e a
63% da sua excursão máxima.
Figura 4.7 Potenciómetros rotativos
Estas posições corresponderiam às posições do cursor móvel no potenciómetro de fita. Neste
caso, temos um potenciómetro de uma só volta, o que significa que 100% da resistência
corresponde a rodar-se o botão de cerca de 270 graus (não 360 graus! Explique por quê!).
Existem outros potenciómetros rotativos que permitem que seja dada mais de uma volta (ver
aulas práticas).
IV/6
Figura 4.8 Potenciómetro rotativo utilizado em circuitos amplificadores áudio.
Em termos de consumo de energia, os potenciómetros consomem energia, tal como qualquer
resistência eléctrica. Se utilizarmos os potenciómetros para controlar o sinal áudio de um
pre−amplificador, de baixo consumo de corrente, a dissipação de energia e calor não são
problemas (por quê?). Contudo, se o potenciómetro se utilizar num circuito de elevado
consumo de corrente, a dissipação de calor é elevada (aplicar a lei de Ohm e ver) e deve-se
ter em conta formas de dissipar o calor gerado.
Figura 4.9 Exemplos de diferente potenciómetros.
Na figura acima mostramos diferentes formas de potenciómetros utilizados em diferentes
circuitos eléctricos.
4.1.4 Problemas.
Problema 4.2
IV/7
a) Calcule as tensões de saída destes dois divisores de tensão (VA e VB), bem como a tensão
entre os pontos A e b (VAB).
b) Se eliminássemos o fio que une os dois circuitos, seria que estes valores se alterariam?
Resposta:
a) VA=65,28 V,
VB=22,26 V e
VAB=42,02 V.
b) Não. Explique
por quê.
Problema 4.3
a) Calcule as tensões de saída dos dois circuitos divisores de tensão (tensão entre A e a
massa e entre B e a massa).
b) Calcule também o valor VAB.
Resolução:
a) VA=65,28 V, VB=75,00V
e.
b) VAB=9,72 V
Problema 4.4
De quanto deverá ser a queda de tensão aos terminais da resistência R1 para que a tensão
VAB=0. E qual o valor de R1?
Resolução
V=9 V e R1=20 KΩ.
Problema 4.5
Um termístor é uma resistência especial em que o valor da sua resistência varia de forma
dramática com a temperatura. Assim sendo, considere o circuito que se segue em que existem
ligados a dois ramos opostos dois termístores iguais (os mesmos coeficientes positivos
térmicos).
IV/8
a) Que tensão deve o voltímetro registrar quando os dois termístores estiverem
exactamente à mesma temperatura?.
b) Qual dos dois termístores deverá estar mais quente para que o voltímetro de uma
leitura negativa?
Resolução
a) V== V
b) Deverá ser o termístor do lado
esquerdo.
4.1.5 Aplicações
Duas das aplicações mais frequentes dos potenciómetros são na calibração de tensões dc e
para medir temperaturas, quando utilizado conjuntamente com um termopar.
No primeiro caso, é aplicado na calibração de fontes de tensão de baixo valor, permitindo a
determinação da curva de calibração.
A curva de calibração não é mais de que um gráfico x-y em que se registam os valores da
corrente em ordenadas e das tensões nas abcissas, fornecidas respectivamente por um
amperímetro e um voltímetro, determinadas por um potenciómetro, que indica os desvios da
corrente relativamente ao seu valor médio (condição de indicação nula, dada por um
Galvanómetro).
Na segunda aplicação o potenciómetro é utilizado para medir temperaturas elevadas. Nestes
casos recorre-se ao uso de um termopar (ver a parte de transdutores) que está em contacto
com a superfície do meio cuja temperatura se pretende determinar, gerando uma pequena
diferença de potencial (de algumas dezenas a centenas de microvolts) que é depois medida
com elevada precisão pelo potenciómetro (usando um indicador do tipo Galvanómetro) e
depois convertida numa indicação de temperatura.
4.2 TENSÕES DE REFERÊNCIA
Um díodo Zener é um díodo de junção pn com propriedades de polarização inversa
controladas, o que o torna extremamente útil em aplicações como dispositivo de referência de
tensão (ver secção 3). Neste caso a tensão aplicada faz-se no modo inverso, de tal forma que
à medida que a tensão de polarização aumenta em amplitude se atinge um valor tal em que a
tensão permanece constante para uma faixa bastante larga de correntes. Isto é, consegue-se
manter uma tensão de referência bastante estável, independentemente da corrente que circula
no circuito teste.
IV/9
Num circuito destes deve-se conhecer primeiramente os parâmetros característicos do díodo
Zener, nomeadamente a corrente e a tensão Vs, de modo a seleccionar-se aquele que melhor
serve a funcionalidade do circuito pretendido. Depois segue-se o dimensionamento do circuito
que consiste em determinar-se qual o valor da resistência a associar-se ao circuito de modo a
limitar a corrente no Zener a um valor predeterminado, bem como a razão de dissipação de
potência no Zener. Isto é:
− V f + I s R + Vs = 0
donde se tira que:
R=
If
V f − Vs
Is
Vs
Vr
deste modo, a razão de dissipação
Is
Vf
de potência é dada por:
P=
2(V f − Vs ) 2
Fonte de
tensão
R
+
Vs
-
Ir
R
em que se inclui o factor 2, como
factor de segurança do circuito.
Problema 4.6
Projecte uma fonte de tensão de corrente continua estável de 10 V, utilizando uma fonte de
alimentação de 15 V e um díodo Zener 1N 961, em que o factor de dissipação de potência é de
400 mW, para uma corrente máxima de 12,5 mA.
Resposta
A primeira coisa, é determinar R a utilizar. Tendo em conta as equações anteriores, obtém-se:
R=
V f − Vs
Is
=
15 − 12
= 400Ω . Agora, devemos saber qual a potência que esta deve
12,5 × 10 −3
suportar. Tendo em conta que P =
2(V f − Vs ) 2
R
=
2 × 32
= 0,125W . Isto é, basta seleccionar
400
uma resistência de 1/8W.
Uma outra forma de se projectar uma fonte de tensão estável é a partir de uma corrente
constante produzida por um circuito transistorizado (bipolar ou unipolar), em que a corrente
de saída se mantém invariável, qualquer que seja a tensão de saída, para além de apresentar
uma resistência bastante elevada, conveniente para se reduzir os erros devidos ao efeito de
carga. Para o caso de um transístor unipolar JFET. Neste casso, pode-se ligar a porta (“gate”)
directamente à fonte (“source”), polarizando-se só a malha da saída. Nestas condições tem-se
Vs=IDR, ou seja:
IV/10
ID =
∆VDS
, onde a resistência de dreno RD,
∆R D
G
D
ID
R
se calcula tendo em conta que RD=∆VDS/∆ID
Vo
S
Vf
4.2.1 Nomenclatura Usual
No que segue, referimo-nos aos termos técnicos mais usuais utilizados e importantes de se
conhecer, no processo de selecção de dispositivos para tensões de referência.
(a) Tensão de alimentação de entrada (Input voltage supply) depende da tecnologia e material
de base usado na concepção do dispositivo activo, em termos de limites superior e inferior
de funcionamento. Tipicamente deve-se ter:
VIN(MIN) = VREF + VDROPOUT
(4.1)
(b) Tensão de referência de saída (reference output voltage), tensão de saída regulada que
deve de estar de acordo com a eq. 4.1.
(c) Exactidão inicial (Initial accuracy), define qual o erro inicial da tensão de saída e define-se
em % ou em mV, para a temperatura de 25ºC.
(d) Corrente de referência de saída (Reference output-voltage).
(e) Carga de referência de Regulação (Reference –load regulation), representa as variações
incrementais da tensão de saída, função da carga utilizada. Exprime-se normalmente em
µV/µA ou mV/mAou ppm/mA, or %/mA.
(f) Regulação de linha de entrada (Input-line regulation), representa as variações incrementais
da tensão de saída devidas a variações da tensão de entrada. Normalmente exprime-se em
µV/V.
(g) Coeficiente de temperatura da tensão de saída (Output-voltage temperature coefficient),
representa as variações na tensão de saída de referência para um dado valor de
temperatura:
TCVOUT = 106 × |VREF(max) / VREF| / (TMAX-TMIN)
(4.2)
Exprime-se normalmente em ppm/°C.
(h) Tensão de saída de elevada estabilidade (Output-voltage long term stability), representa
variações na tensão de referência de saída em função do tempo. Normalmente exprime-se
em ppm/horas.
(i) tensão de ruído de saída (output noise voltage), corresponde ao valor de tensão esporádico
que aparece sobreposto ao sinal. É função da frequência do sinal utilizado e exprime-se em
µVRMS na faixa de frequências de 10Hz a 10kHz.
IV/11
(j) Faixa de estabilidade e de carga capacitiva (Capacitive-load Stability range) corresponde à
faixa de capacidades de carga (inclui também efeitos parasitas) que a tensão de referência
pode tolerar, sem alterar o seu valor ou forma.
4.2. Erro de saída e definições de precisão de uma referência
Designamos por erro o desvio da condição ideal de uma dada tensão de saída. Em circuitos
digitais tal significa que a resolução pretendida é a do bit. Assim, num circuito de 12- bit, a
saída possível é de 4096. Se associarmos a cada valor numérico um 1mV, significa que o valor
máximo da tensão de saída será de 4,096 V, com uma tensão de referência de 4,096V.
Qualquer desvio deste valor corresponderá a um erro.
Em termos de exactidão, considerando que o bit menos significativo (LSB) é 1mV e se
designarmos a precisão final da medida como sendo de ±4SLB (±4mV), a exactidão da medida
corresponderá a sabermos com que exactidão de bits a saídas poderá ser processada:
Exactidão = Resolução da fonte - log2(erro)
(4.3)
Neste exemplo significa que só temos 10 bits (12 - log2(4)) de precisão.
Figure 4.10 Função de transferência e erro de saída em fonte DAC
Existem várias fontes que contribuem para o erro da tensão de saída (tal como o “offset” da
fonte), mas algumas são ignoradas, pois são irrelevantes para o processo de selecção da
tensão de referência. As fontes de erro que são normalmente consideradas não incluem: erro
inicial da referência; histerese térmica; estabilidade a longo prazo; regulação da linha e da
carga; ruído de entrada e saída.
IV/12
Bibliografia
H. Young and R. Freedman. Sears and Zemansky's University Physics with modern physics
(10th edition). Addison Wesley Longman, Inc., pages 799-864, 2000.
H. Young and R. Freedman. Sears and Zemansky's University Physics with modern physics
(10th edition). Addison Wesley Longman, Inc., pages 799-864, 2000.
4.2.1 Caixa de tensões
A faixa de tensões em que o potenciómetro é directamente utilizado para determinar tensões
desconhecidas é muito baixa (1 a 3 V). Assim, quando se pretendem determinar tensões
desconhecidas de valor elevado, tal não é possível. Nestas condições, recorre-se a um
instrumento designado de caixa de tensões.
A caixa de tensões é um instrumento de precisão que opera no principio de indicação nula,
utilizado para determinar valores de tensões desconhecidas. O seu principio de funcionamento
está associado ao do potenciómetro. Neste caso concreto a tensão desconhecida (Vx) a
determinar é ligada em série a uma resistência conhecida variável (reostato). Aos terminais do
reostato é ligado então um potenciómetro (V2). Como se tem uma ligação em série, a corrente
que passa no circuito, que contém a tensão desconhecida e, na resistência R2, de parte do
reostato (Rr=R1+R2) ligado ao potenciómetro, é a mesma.
Nestas condições tira-se que:
Vx R 1 + R 2
=
V2
R2
(4.4)
Problema 4.7
Uma caixa de tensões foi projectada de modo a que quando uma tensão desconhecida de 100
V é aplicada à entrada desta, a tensão de saída seja de 2 V. Nestas condições, determine o
valor da resistências a utilizar.
Resolução
De acordo com a equação 4.4 tem-se que Vx/V2=50, donde se tira que (R1+R2)/R2=50 e
portanto R1=49R2
4.3 . PONTES DE CORRENTE CONTINUA
4.3.1 Ponte de Wheatstone
Circuitos pontes são instrumentos utilizados para comparar medidas de componentes passivos
e baseiam-se no princípio de indicação nula. Isto é, a sua indicação é independente da
calibração do dispositivo detector, pelo que o seu grau de precisão é muito elevado. Tal faz
com que sejam utilizados no controlo de diferentes circuitos de medida, em que num dos
ramos existe a componente a medir, sensível a um parâmetro físico (pressão, temperatura,
etc.) e nos outros, componentes passivos reguláveis, previamente conhecidos.
IV/13
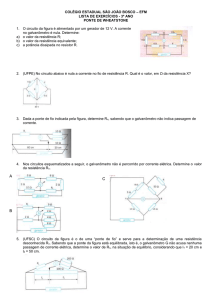
A ponte de Wheatstone consiste em dois ramos paralelos de resistências, cada um contendo
duas resistências em série. A estas resistências é aplicada uma tensão continua de modo a
provocar a passagem de correntes nos ramos.
Entre os ramos em paralelo liga-se um
detector (galvanómetro) de modo a
I1
R1
R2
I2
determinar a condição de balanceamento
(corrente nula). Este circuito foi inventado em
V
G
1833 por S.H. Chriestie em 1833 e só posto
em prática a partir de 1847 por Sir Charles
I3
R3
Wheatstone.
I4
R4
Quando a ponte está balanceada isso significa que não passa qualquer corrente no
galvanómetro e que o potencial neste é nulo. Nestas condições, isso significa que I1=I3 e I2=I4
e I3R3=I4R4; I1R1=I2R2, pelo que se tem:
R1 R2
=
, ou R1R4=R2R3
R3 R4
(4.5)
Assim, caso um dos valores da resistência seja desconhecido, é possível determinar-se, por
ajuste de valor de uma das resistências do ramo oposto.
Problema 4.8- Considere a ponte de Wheatstone representada na figura. Se R1=15KΩ,
R2=10KΩ,R3=30KΩqual deverá ser o valor de R4 para a ponte estar equilibrada.
Resolução
De acordo com o que foi dito anteriormente tira-se que R4 =
R2 R3 10 × 30
=
= 20kΩ .
15
R1
Quando uma dada ponte não está balanceada, passa corrente pelo galvanómetro, que faz com
que haja uma deflexão do seu ponteiro, proporcional à quantidade de corrente que por lá
passa. Define-se sensibilidade da ponte à deflexão por unidade de corrente que passa pelo
galvanómetro. Isto quer dizer que quanto mais sensível o galvanómetro for, maior será a sua
deflexão, para a mesma quantidade de corrente. Isto é, D=S×I, onde D é a deflexão, S a
sensibilidade da ponte e I a corrente que por lá passa.
Nas condições de não balanceamento, I1≠I3 e I2≠I4. Para além disso, a diferença de potencial
aos terminais do galvanómetro (Vab) não é nula. Nestas condições, para a determinação das
correntes que passam neste circuito devemos recorrer às malhas de Kirchoff às quais se deve
aplicar o teorema de Thevenin, para simplificação das malhas resultantes (análise reduzida ao
comportamento de uma fonte de tensão equivalente ligada em série com uma resistência
equivalente). Por análise do circuito, a tensão equivalente de Thevenin aos terminais do
galvanómetro é a tensão vista aos terminais ab, quando estes estão em circuito aberto. Isto é:
IV/14
Vab = Va − Vb , onde Va = V
R3
R4
e Vb = V
.
R1 + R3
R2 + R4
(4.6)
A resistência equivalente de Thevenin é aquela que é vista aos terminais de saída quando
todas as fontes do circuito são substituídas por curto circuitos. Nestas condições, a resistência
final é a resultante da associação em série das combinações em paralelo de R1 com R3 e R2
com R4. Isto é:
RTh =
R1 R3
R R
+ 2 4 .
R1 + R3 R2 + R4
(4.7)
Se 3 das quatro resistências da ponte forem iguais a um dado valor Re e, se a quarta diferir
destas de um valor inferior a 5%, é possível desenvolvermos uma expressão quer para Vth e
Rth: Isto é: VTh≈V(∆r/4R) e RTh≈R.
Problema 4.9
Em termos gerais diga o que deve ser feito para balancear a ponte que se mostra na figura
que se segue. O que realmente significa, neste contexto, o termo balanceamento?.
Resolução
A ponte estar balanceada significa que a diferença de
potencial entre os dois extremos do circuito, assinalados,
não ligados à fonte de alimentação, é nula.
O atingir-se a condição de balanceamento significa que a
razão das resistências adjacentes dos quatro braços que
constituem o circuito são proporcionais e iguais entre si,
pelo que não circula qualquer corrente pelo medidor,
também.
Problema 4.10
O que é que acontece à tensão entre os pontos A e B se se aumentar a tensão da fonte de
alimentação?
Resolução.
A razão entre as resistências adjacentes é
constante e igual entre si, logo a ponte está
balanceada. Assim, nada acontece por se
aumentar a tensão da fonte de alimentação.
VAB=0 V.
Problema 4.11
IV/15
Complete as ligações do circuito que se mostra de forma a que a ponte formada fique
balanceada.
Resolução
4.3.2 PONTE DE KELVIN
A ponte de Kelvin é uma versão modificada da ponte de Wheatstone, de modo a eliminar o
efeito das resistências dos contactos e dos cabos de ligação, do processo de medida, quando
se pretende determinar com rigor o valor de resistências de muito baixo valor (µΩ). Para
compensar os efeitos acima enumerados, esta ponte usa um segundo par de ramos de forma a
compensar o valor das resistências de contacto e dos cabos.
A ponte está balanceada quando se verifica:
R4 R3 Rb
=
=
R2 R1 Ra
R2
I1
(4.8)
R1
I2
V
c
Ra
Rk
G
c
Rb
I3
R3
R4
I4
4.3.3 Circuito de um quarto de ponte
Na configuração do circuito de um quarto de ponte, um dos braços do circuito varia com o
parâmetro físico que se pretende medir e os outros permanecem constantes.
Nestas condições tem-se:
Vbo/Vex = (Rc/(Rc+Rg+dRg)- (1/2)
(4.9a)
A ponte diz-se estar balanceada quando Rc é escolhida de forma a se adaptar a Rg. Rg
representa o que resta da resistência do transdutor, em termos de compensação do circuito
ponte. Para medição de forças de tensão mecânica, quando Rc=Rg, a equação anterior pode
ser expressa em termos do factor de calibração (Gf) dando:
IV/16
Vbo/Vex = Gf/(4 +2 Gf)
(4.9b)
Dependendo das especificações do transdutor utilizado, a tensão de alimentação é de 5 V e o
consumo de corrente típico é de 50 mA.
Na configuração de meia ponte um dos braços é constituído por dois sensores e o outro por
duas resistências fixas. Neste caso tem-se:
Vout/Vex = Gf/2
(4.9c)
Problema 4.12
Um transdutor de força de tensão é um aparelho capaz de ler a força de compressão ou
extensão a que um dado objecto está sujeito, ao dar lugar a uma variação da resistência
proporcional ao valor da força em causa. No que se segue mostra-se um transdutor de pressão
ligado a um circuito de um quarto de ponte enquanto os outros ¾ correspondem a
componentes fixos. Explique o que aconteceria à tensão medida na ponte se o transdutor
estiver em compressão, pressupondo que inicialmente a ponte está balanceada, sem qualquer
força de compressão aplicada.
Resolução
À medida que a força de compressão aumenta
a ponte fica não balanceada, passando o
voltímetro a indicar uma medida não nula de
polaridade independente da natureza da força
utilizada!
Problema 4.13
Suponha que tem um circuito ponte em que um dos braços da ponte está ligado a um
transdutor de pressão compressivo. O que acontece à tensão VAB se a temperatura da amostra
variar (mesmo sem aplicação de qualquer força), partindo do pressuposto que inicialmente a
ponte se encontrava balanceada? Considere que o coeficiente α de temperatura da resistência
do sensor é positivo. Comente da exequibilidade de utilização deste sistema como instrumento
de medida de forças de tensão.
IV/17
Resolução
Se o sensor aquece, desenvolve-se uma
tensão aos terminais A e B tal que o
terminal A é positivo e B é negativo (por
quê?)
Problema 4.14
Explique de que forma o circuito que se segue poderia ser utilizado para compensar
automaticamente variações de temperatura num sensor de pressão.
Resolução
Para se satisfazer as condições requeridas, é
necessário que exista no circuito um sensor
de sacrifício (dummy) ligado à amostra a
caracterizar, de tal maneira que não seja
sujeito às mesmas condições de trabalho do
sensor, que irá medir a força de tensão. Este
está somente sujeito às mesmas condições de
temperatura da amostra e reagirá somente a
estas
variações.
Deste
modo,
qualquer
variação da temperatura será compensada
por este, pelo que a indicação do voltímetro
será deste modo insensível à temperatura.
Problema 4.15
Considere o circuito que se mostra a seguir onde se supõe que a tensão aos terminais
corresponde
à
diferença
entre
a
tensão
gerada
pelas
duas
fotocélulas
(elementos
transdutores). Contudo, neste circuito alguma coisa falhou, pois a indicação do voltímetro é
sempre negativa e não varia ao variar-se a iluminação a qualquer um dos sensores. Indique
pelo menos duas possibilidades que possam justificar o comportamento detectado.
IV/18
Resolução
O
comportamento
observado
deve-se
ou
à
resistência R1 que está em curto circuito (por quê?)
ou por que a fotocélula R3 se encontra em circuito
aberto (por quê?).
4.3.4 Aplicações de pontes na determinação de parâmetros distribuídos de
cabos
Uma das principais aplicações das pontes dc é na determinação da resistência distribuída em
cabos eléctricos, para determinação de falhas nestes. Estão neste caso as chamadas malhas
de Murray e de Varley.
Figura 4.11 Exemplo da malha de Murray para determinação de curto circuitos à massa em cabos de
comunicações
IV/19
A
malha
de
Murray
é
utilizada
para
determinar curto circuitos entre linhas ou à
massa. Neste caso o condutor com defeito
possui um comprimento L está ligado aos
terminais
de
um
bom
condutor
de
comprimento LA. A malha formada pelos dois
condutores está ligada à ponte como se
mostra nas figuras, sendo a ponte balanceada
por ajuste da resistência do B (RB). Se
designarmos
por
RA,
RLa,
RL
e
RX
respectivamente as resistências do braço A da
ponte, do braço associado ao bom condutor,
resistência
total
defeituoso
e
associada
Resistência
ao
condutor
associada
ao
comprimento X do mau condutor, na condição
de balanceamento tem-se:
RX =
RA
( R La + RL )
R A + RB
4.10a
Por outro lado, se os dois condutores forem do mesmo material e tendo em conta que R=ρl/S
em que l é o comprimento do condutor e S a sua secção, tem-se:
X =
RA
( L + La )
R A + RB
4.10b
Assim, para um cabo de multicondutores, todos com o mesmo comprimento, a distância a que
se encontra o curto circuito à massa do ponto de ligação à ponte é dado por:
X =
2 LR A
R A + RB
4.10c
O outro circuito utilizado na detecção de falhas em cabos e a malha de Varley. Trata-se de
uma modificação da malha de Murray em que se utiliza uma razão constante dos braços
adjacentes contendo resistências fixas e no outro, adjacente ao cabo ma inspeccionar, liga-se
um reostato. Este circuito é mais utilizado para localizar curto circuitos entre condutores ou à
massa e é mais preciso que o anterior.
IV/20
Figura 4.12 Malha de Varley
Nestas condições, tem-se em balanceamento:
RX =
R B ( R g + Rb ) − RR A
(4.11a)
R A + RB
Se ligarmos agora o terminal GR ao outro extremo do braço B e balanceando de novo a ponte
tem-se:
R g + Rb =
RA R
RB
(4.11b)
Deste modo é preciso localizar o condutor e a posição em que se deu a falha.
4.4. PONTES DE CORRENTE ALTERNA
No caso da ponte de Wheatstone ser formada por quatro impedâncias não resistivas, esta pode
ser utilizada para determinar condições de balanceamento em circuitos de corrente alterna.
Neste caso, o detector a utilizar deve ser de corrente alterna. As pontes de corrente alterna
são circuitos muito usados em circuitos eléctricos de deslocamento de fase, como meio de
realimentação em circuitos eléctricos Osciladores ou em amplificadores, filtros de sinais
eléctricos e para medição da frequência de sinais áudio.
A condição de balanceamento é similar à
obtida
para
a
ponte
de
Wheatstone,
substituindo R por Z (impedância). Nestas
condições tem-se Z1Z4=Z2Z3. Se tivermos em
conta que a impedância tem uma componente
real e outra imaginária e portanto, se pode
representar sob a forma Z= Zejθ=a+jb, da
relação anterior obtém-se:
Z 1 e jθ 1 Z 4 e jθ 4 = Z 2 e jθ 2 Z 3 e jθ 3 ,
(4.12)
IV/21
donde se conclui que para a ponte estar balanceada é necessário que Z1Z4=Z2Z3.e θ1+θ4=θ2+θ3.
Outra forma de chegar ao mesmo resultado é o de se considerar a impedância como uma
grandeza complexa, com componente real e imaginária. Nestas condições tem-se:
(a1 + jb1 ) × (a 4 + jb4 ) = (a 2 + jb2 ) × (a3 + jb3 ) ,
(4.13a)
donde se obtém:
(a1 a 4 − b1b4 ) + j (a1b4 + a 4 b1 ) = (a 2 a3 − b3b2 ) + j (a 2 b3 + a3 b2 ) ,
(4.13b)
igualdade que só é verdadeira quando as partes reais e imaginárias são iguais entre si. Isto é:
(a1 a 4 − b1b4 ) = (a 2 a3 − b3 b2 )
(4.14a)
e
(a1b4 + a 4 b1 ) = (a 2 b3 + a3 b2 )
(4.14b)
As pontes de impedância são similares às pontes dc. Neste caso o detector a utilizar deve ter a
capacidade de discriminar pequenos sinais ac. Muitas vezes utiliza-se para o efeito
osciloscópios ou mesmo auscultadores se a frequência a detectar está dentro da faixa áudio.
Neste caso estes são ligados ao circuito através de um transformador/adaptador de
impedância. Os auscultadores possuem normalmente uma baixa impedância de carga (cerca
de 8 Ω), pelo que requerem também correntes elevadas. Tal faz com que se recorra a um
transformador áudio de saída (valores típicos: 220/6 Volts e razão de impedâncias de 1000:8).
Deste modo, é possível detectar-se correntes tão baixas como 0,1 µA e sinais dc a ac com
f=2 MHz.
Figura 4.13 Ponte ac com detector à base de auscultadores áudio.
A condição de balanceamento é obtida quando deixar-se de se ouvir “clicks” nos
auscultadores.
IV/22
4.4.1 Diferentes tipos de pontes de corrente alterna
Os circuitos ponte servem também para medir indutâncias, capacitância e mesmo o factor Q
de um circuito. Tal como nos circuitos anteriores a impedância desconhecida deve ser sempre
balanceada, em termos de um valor padrão conhecido. Dependendo do modo como a ponte é
ligada a componente desconhecida pode ser determinada directa ou indirectamente. Nos dois
exemplos que se seguem, determina-se o valor de uma indutância ou de uma capacidade
desconhecidas a partir de padrões conhecidos indutivos ou capacitvos, respectivamente.
Neste caso as pontes dizem-se simétricas, pois a determinação da reactância desconhecida é
feita por acerto directo do padrão similar utilizado.
Figura 4.14 Exemplos de pontes ac para determinação de indutâncias e capacidades desconhecidas, a
partir de padrões conhecidos.
Contudo, em casos práticos, essa não é a situação normal.
4.4.1.1 PONTE DE PEQUENOS ÂNGULOS
Esta ponte é utilizada para medir a impedância capacitiva de circuitos eléctricos. Neste caso, 2
ramos adjacentes da ponte são puramente resitivos (Z1=R1 e Z2=R2) e os outros dois,
impedâncias capacitivas (Z3=R3-j/ωC3) e Z4=Rx-j/ωCx). Nestas condições, e de acordo com o
que foi anteriormente dito, a condição de balanceamento implica que:
R1 R x = R2 R3
e
R1
R
= 2 . Isto é, Cx=C3(R1/R2). A determinação da capacidade
ωC X ωC 3
desconhecida é independente da amplitude e frequência do sinal alterno aplicado à ponte.
A Rx também se designa de resistência série equivalente da impedância desconhecida, por
representar a parte real da componente de impedância total.
A Cx designa-se de capacidade equivalente da impedância desconhecida, por representar a
reactância total da impedância.
IV/23
4.4.1.2 PONTE DE MAXWELL
Esta ponte é utilizada para determinar o valor de indutâncias desconhecidas, à custa de
capacidades padrão.
Neste caso, dois dos ramos justapostos da ponte
são puramente resistivos e nos outros dois, num
deles existe a indutância de valor desconhecido e
no outro a capacidade padrão, associada em
paralelo com uma resistência variável.
Nestas condições, a condição de balanceamento
conduz-nos
R1 R x = R2 R3
a:
e
Lx=C1R3R2,
também independente do valor da frequência e
amplitude do sinal alterno aplicado á ponte. Tal
como
anteriormente,
Lx
representa
a
componente indutiva equivalente em série (pois
pressupõe-se que as componentes desconhecias
se encontram assim associadas).
Nota: em
termos práticos faz-se com que R1=R2=R3.
4.4.1.3 PONTE DOS ÂNGULOS OPOSTOS OU DE HAY
Esta ponte serve também para medir indutâncias e resistências de bobinas desconhecidas em
que o factor de qualidade de bobinas [razão entre a reactância (XL) e a resistência da bobina:
Q=XL/R] seja superior a 10.
É uma ponte similar à de Maxwell (utilizada
quando
Q<10)
mas
neste
caso,
R1
a
I1
capacidade padrão encontra-se associada
em série com uma resistência.
I2
V
D
Neste caso, a condição de balanceamento
conduz-nos às relações: R x
=
ω RR RC
1+ω R C
2
2
1 2 3 1
2 2 2
1 1
R2 R3 C1
.
e Lx =
1 + ω 2 R12 C12
Neste
caso,
os
valores
obtidos
dependentes da frequência.
Nota: R1=RB; R3= Rs; R2=RA; C1=Cx.
IV/24
são
R2
C1
Rx
I3
I4
R3
Lx
Isto é, os valores de resistência e indutância desconhecidos dependem do valor da frequência
do sinal alterno aplicado à fonte.
4.4.1.4 PONTE DE WIEN
Trata-se de uma fonte versátil, utilizada para medir componentes de impedâncias, quer
associados em série, quer associados em paralelo.
Esta ponte é largamente utilizada em circuitos
eléctricos
de
realimentação,
para
R1
provocar
I1
R2
I2
oscilação do sinal eléctrico, a uma frequência préV
determinada.
Neste
caso,
a
condição
de
balanceamento
corresponde a:
Rx =
R3
R2
R
1
e C x = 1 (C 3 +
)
2 2 2
2 2 2
R1 1 + ω R3 C 3
R2
1 + ω R3 C 3
D
Rx
I3
R3
C3
I4
Cx
onde os valores de resistência e capacidade
desconhecidos dependem da frequência do sinal
alterno utilizado.
Em circuitos práticos tem-se R1=R2=R, passando o
circuito a ter a forma que ao lado se mostra.
4.4.1.5 PONTES DE RÁDIO FREQUÊNCIA
As pontes de rádio frequência são similares às pontes de Wien, sendo R1 substituído pela
combinação paralelo de uma resistência e um condensador variável e a combinação R3 e C3
substituída por uma única resistência.
IV/25
Neste caso, a impedância desconhecida Zx=Rx±jXx é
R1
C1
inserida no ramo previamente balanceado, através
de R4 e C4 e a condição de balanceamento
corresponde a:
R2
I2
I1
V
D
R4
I3
R
1 1
1
R x = 3 (C1' − C1 ) e X x = ( ' − )
C2
ω C4 C4
I4
R3
C4
Zx
'
'
onde C1 e C 4 são os valores de C1e C4 reajustados após a inserção na ponte de Zx. Assim,
constata-se que enquanto a determinação da componente resistiva de Zx é independente da
frequência do sinal aplicado à ponte, a determinação da componente reactiva depende da
frequência do sinal alterno aplicado à ponte.
Deve-se também ter em conta que a natureza da reactância desconhecida depende do sinal de
Xx. Se C’4>C4, então o sinal de Xx é negativo e a reactância é capacitiva, pelo que Cx=1/(ωXx).
Se C’4<C4 então Xx é positivo e a reactância é indutiva, pelo que Lx=Xx/ω.
Problema 4.16- Considere a ponte de rádio frequência que acima se mostra. Sem inserção de
Zx, para f=10 MHz, os valores de balanceamento obtidos são R1=120 KΩ; C1= 100 µF; C2= 7,5
µF; R3= 7,5 KΩ; C4= 120 µF; R4= 100 KΩ. Por inserção de Zx a ponte teve de ser de novo
balanceada, ajustando C1 e C4 respectivamente para 110 µF e 102,4 µF.
Calcule os valores dos componentes da impedância desconhecida
Resolução
De acordo com as expressões anteriores obtém-se: Rx= 10 KΩ e Xx= 22,8×10-6, donde se
conclui que a reactância é indutiva (por quê?), onde Lx= 3,63×10-13 H.
4.4.1.6 PONTE DE SCHERING
A ponte de Schering é particularmente importante na determinação das propriedades
dieléctricas de materiais. Isto é, em componentes em que o angulo de desfasagem da
impedância se encontra muito próximo dos 90º.
Nestas condições tem-se:
R x = R2
C1
C3
e
C x = C3
R1
C1
R1
. Isto é, os
R2
valores são independentes da frequência
R2
I2
I1
V
D
do sinal alterno aplicado á ponte
Rx
I3
I4
C3
Cx
IV/26
Problema 4.17- Considere o circuito que a seguir se mostra. Determine as constantes de Zx R
e C ou L, considerando as mesmas como estando associadas em série.
Resolução
Tendo
em
R2 =200Ω
conta
os
valores
R1=200Ω
apresentados na figura, a impedância
em
questão
é
capacitiva,
Rx=122,6 Ω e Cx=0,33 µF.
onde:
I2
I1
V=6 V
f=1KHz
C2 =5µF
D
R3=500Ω
I4
I3
Zx
C3 =0.2µF
Problema 4.18- repita o problema 4.17, mas agora com Z1= 400ej0 Ω; Z2=300e-j40 Ω;
Z3=100e-j20.
Resolução
Tendo em conta que Z1Zx=Z2Z3, obtém-se Zx=(Z2Z3)/Z1=75e-j60, conclui-se que para este caso
a impedância continua a ser do tipo capacitivo onde Rx=37,5 Ω e Cx=15,4 µF.
Sites a Consultar
http://sound.westhost.com/pots.htm
http://www.ece.drexel.edu/courses/ECE-E432/Lab2_Sources.html
http://www.aslltd.co.uk/acvdc.htm
http:// www.aslltd.co.uk/pdf/Acvdc.pdf
http:// physics.ucsd.edu/~drs/Classwork/ 120A_Lab2_Week3_Spr_04.pdf –
www.allaboutcircuits.com/vol_2/chpt_12/5.html - 27k
IV/27