Circuitos Elétricos

Circuitos Elétricos
1) Introducão
Revisão sobre elementos
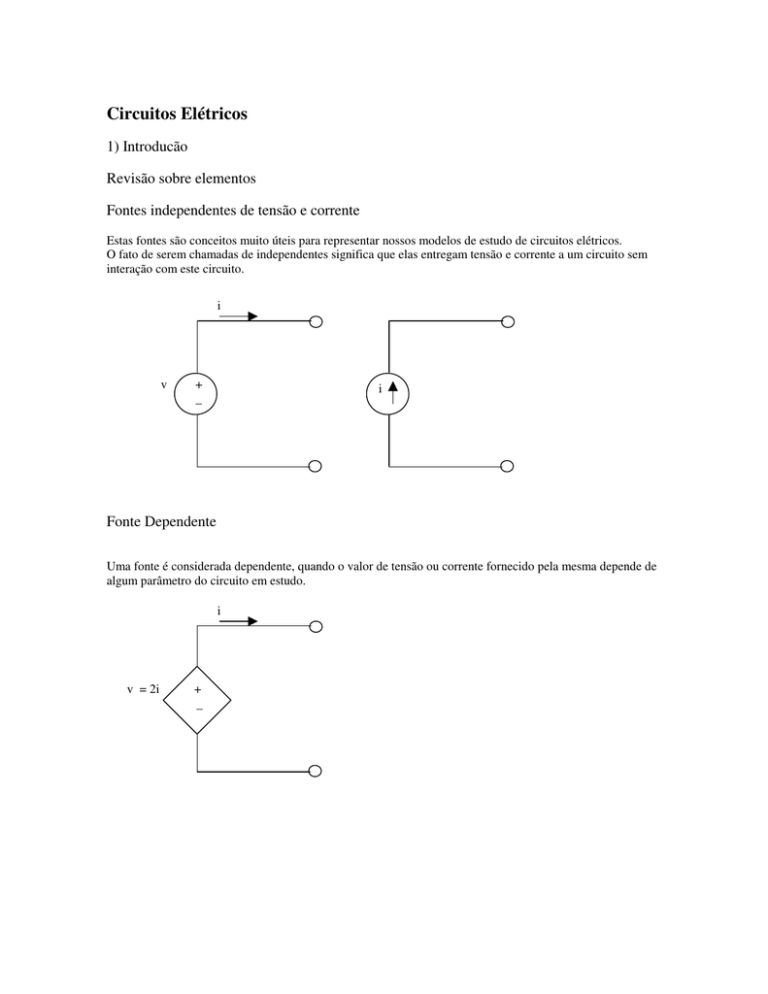
Fontes independentes de tensão e corrente
Estas fontes são conceitos muito úteis para representar nossos modelos de estudo de circuitos elétricos.
O fato de serem chamadas de independentes significa que elas entregam tensão e corrente a um circuito sem
interação com este circuito.
i
v
+
_
i
Fonte Dependente
Uma fonte é considerada dependente, quando o valor de tensão ou corrente fornecido pela mesma depende de
algum parâmetro do circuito em estudo.
i
v = 2i
+
_
Circuitos CC e CA
Os circuitos de corrente contínua são aqueles que são submetidos a uma fonte de tensão ou corrente que ao
longo do tempo não alternam sua polaridade.
v
i
v
R
tempo
i
tempo
Os circuitos de corrente alternada são submetidos a fontes que alternam sua polaridade ao longo do tempo.
v
v
200
150
100
50
0
-50 0
-100
-150
-200
180
360
Resistores
Resistores elétricos são dispositivos usados em circuitos elétricos, onde se aproveita a sua resistividade
para servir como carga, ou mesmo como limitador de corrente, sendo que sua resistência ao fluxo de elétrons
é devidamente conhecida e medida em ohms (Ω) e simbolizado em circuitos pela letra R.
O termo carga agora passa a representar o dispositivo elétrico capaz de consumir energia elétrica.
Como carga elétrica, os resistores convertem a energia elétrica em calor, como exemplo, temos o ferro
elétrico, chuveiro e forno a resistência, ou em luz como é o caso das lâmpadas incandescentes, que apesar de
converter a energia elétrica em energia luminosa, ela tem um baixo rendimento, isto porque quase que a
totalidade da energia fornecida é convertida em calor, um percentual em torno de 95%. E apenas 5%
aproximadamente é utilizado como luz.
Todos estes efeitos, podem ser entendidos com uma simples interpretação da lei de ohm, ou seja, V =
R.I, onde para alterar o valor da corrente sem modificar valor da tensão, trabalha-se com R.
_______________________________________________________________________________________
REVISÃ0
RESISTÊNCIA ELÉTRICA
Ao provocarmos a circulação de corrente por um material condutor através da aplicação de uma
diferença de potencial, pode-se observar para um mesmo valor de tensão aplicada em condutores de diversos
materiais que a corrente possuirá valores diferentes. Isto ocorrerá devido as características intrínsecas de cada
material.
Este comportamento diferenciado da corrente, deve-se à resistência elétrica de cada material, que
depende do tipo de material do condutor, comprimento, área da seção transversal e da temperatura.
Esta resistência atua como uma dificuldade à circulação de corrente elétrica, ou à circulação de
elétrons.
Para haver uma melhor interpretação do fenômeno de resistência, deve-se analisar os aspectos
macroscópicos e microscópicos dos diversos materiais.
Os aspectos microscópicos referem-se à estrutura da rede cristalina, do número de elétrons livres do
material e a movimentação destes elétrons livres no interior do condutor. Quando os elétrons livres são
impulsionados a movimentar devido a ação de uma tensão ocorrerão choques entre os próprios elétrons livres
e a rede cristalina, então como efeito disto, ter-se-á uma dificuldade ao deslocamento dos elétrons.
Assim sendo, as características microscópicas que influenciam no deslocamento dos elétrons livres
são:
• a forma como estão organizados os íons na rede cristalina.
• o espaçamento disponível para o movimento dos elétrons livres.
• sua velocidade média de arrastamento.
• número de íons e de elétrons livres disponíveis por unidade de volume.
Os fatores macroscópicos são:
• tipo do material que constitui o condutor
• comprimento
• área da sua seção transversal
• temperatura
• tensão elétrica
Todos estes fatores irão caracterizar a resistência elétrica do material.
1A LEI DE OHM
O estudo da resistência é de grande valia na determinação da potência dos diversos equipamentos
elétricos.
A expressão, matemática que permite a obtenção da grandeza resistência é a seguinte:
V = R . I , ou seja, R =V , onde
I
R - é a resistência elétrica, dada em ohms, cujo símbolo é Ω (letra ômega).
V - é a tensão elétrica nos terminais do dispositivo, dada em volt, cujo símbolo é V (letra V).
I - é a intensidade de corrente que circula pelo dispositivo, dada em ampères (letra A)
2A LEI DE OHM
Para determinação da resistência, valendo-se dos parâmetros macroscópicos, tem-se a seguinte
expressão conhecida como segunda lei de ohm:
λ
S
λ
R = ρ , onde
S
ρ - (letra grega rô) é a resistividade específica do material dada em ohm vezes metro (Ω.m).
λ - é o comprimento em metros (m).
S - é a área da seção transversal em metros quadrados (m2).
Através da observação da expressão, pode-se verificar que o valor da resistência é diretamente
proporcional ao comprimento e inversamente proporcional a área da seção transversal, em outras palavras,
quanto maior o comprimento, maior a resistência. Quanto maior a área da seção transversal, menor a
resistência.
A variação da resistência em função do comprimento do condutor pode ser explorada em transdutores
conhecidos como extensômetros.
TABELA Resistividades ρ e Coeficientes de temperatura α
ρ (20º) Ω.m
α (20º) k-1
Alumínio
2,8.10-8
3,9.10-3
chumbo
22,0.10-8
4,3.10-3
cobre
1,7.10-8
3,9.10-3
ferro
10,0.10-8
5,0.10-3
prata
1,6.10-8
3,8.10-3
100,0.10-8
0,4.10-3
640
-7,5.10-2
MATERIAL
nichome (Ni, Cr, Fe)
silício
VARIAÇÃO DA RESISTÊNCIA EM FUNÇÃO DA TEMPERATURA
A influência da temperatura é demonstrada na expressão a seguir.
R = R0 (1 + α ∆θ) , onde
R - é a resistência na temperatura final expressa em ohms (Ω)
R0 - é a resistência na temperatura inicial expressa em ohms (Ω)
α - coeficiente de variação da resistência com a temperatura, expressa
em graus Celsius elevado a menos um (oC-1)
∆θ - é a variação da temperatura, ou seja, é a temperatura final menos a
temperatura inicial, expressa em grau Celsius (oC).
Como exemplo: Um fio de cobre tem resistência de 100Ω a 20oC. Considerando α = 3,9.10- 3 oC- 1
para o cobre e temperatura final de 100oC, então sua resistência final será :
R = 100 . ( 1 + 3,9.10- 3 . 80 ) = 131,2 Ω
O que normalmente se observa nos condutores metálicos é o aumento da resistência em função do
aumento da temperatura. Isto pode ser explicado pelo estado de agitação térmica da estrutura cristalina do
material. Portanto, quanto maior o estado de agitação cristalina do material, maior será a resistência para uma
grande maioria dos casos.
Algumas aplicações da propriedade da resistência são mostradas a seguir:
• fusíveis
• lâmpadas incandescentes
• resistores para aquecimento (fornos, estufas, chuveiros, etc.)
• sensores de temperatura ( termo-resistores )
Para a realização de medidas diretas de resistências pode-se usar o ohmímetro ou a ponte de
Wheatstone.
Capacitores
Capacidade de armazenar carga elétrica.
C=
q
coulomb
(F)
v
volt
v=
q
C
dv 1 dq
=
dt C dt
i=C
dv
dt
1
i dt
C
dv =
v
t
∫ dv
v0
1
=
C
∫ idt
t0
t
v =
1
C
∫ idt + v0
t0
Indutores
Indutância
L=
λ
i
(H-henries)
λ = fluxo magnético
Indutores : bobinas para tirar proveito da indutância
dλ
(lei de faraday)
dt
dλ d ( Li )
di
v=
=
=L
dt
dt
dt
v=
di =
v
L
i
t
∫
di = 1
L
i0
1
i=
L
dt
∫ vdt
0
t
∫ vdt + i
0
0
Exemplo de Carga e Descarga de um Capacitor
Desenhe como ocorre a carga e a descarga de um capacitor no circuito abaixo.
Qual é a constante de tempo do circuito?
100 Ω
S
50 Ω
+
1µ F
10V
-
Carga do Capacitor
R
i
v2
V
c
v
V= v + v2 = v + R . i
Para
i=c
dv
dv
=> V = v + R . C
dt
dt
dv
1
V
+
v=
dt RC
RC
Solução da equação diferencial :
v = vh + vp
( Solução da equação é igual a soma das soluções homogêncea com a
particular )
Solução Homogênea ( vh ):
dv
v
+
=0
dt RC
vh = A.est
s.A.est +
1
.A.est = 0
RC
A.est (s +
1
)=0
RC
=>
s =
−1
RC
vh = A.e-t/RC
Solução Particular ( vp ) :
vp = B (cte)
0+
B
V
=
RC
RC
=>
B = V = vp
v = vh + vp = A .e-t/RC + V
p/
t = 0+ => v (0+ ) = A + V => A = v (0+ ) – V
v = (v (0+ ) –V ).e-t/RC + V
p/
v (0+ ) = v (0- ) = 0
v = V (1 - e-t/RC )
v
V
t
Um conceito muito utilizado é o da constante de tempo de um circuito que é representada
por t = RC , significando que após t segundos a tensão no capacitor inicialmente
descarregado chegará a 0,63 V e a corrente decrescerá p/ 0,37 V/R
Descarga do Capacitor
v
v + v2 = 0
v+R.i=0
v+R.C
dv
= 0
dt
dv
1
+
.v = 0
dt
RC
Solução: v = vh + vp
vh :
vh = A.est
s.A.est +
A.est (s +
1
. A.est = 0
RC
1
)=0
RC
=>
s=
vp :
vp = B
0+
1
.B =0
RC
v = vh + vp
=> B = 0
−1
RC
v2
R
v = A.e-t/RC
t = 0+ => v (0+ ) = A
p/
v (0+ ) = V =>
A=V
v = V .e-t/RC
v
V
x
Exercício
Determine a tensão de carga do capacitor, quando em t = 0, i (0) = 0, vc (0) = 0, e dvc (0)/dt = 0
v(t)
S
R
L
+
-
C
V
Tarefa Complementar
Estudo do Texto Acadêmico:
Giacomin, J. Vieira, O.J .Princípios de Eletricidade. Editora UFLA/FAEPE
Leitura e exercícios dos Capítulos 1 e 2 de:
O’Malley, J. Análise de Circuitos 2ª. Ed. Schaum McGraw-Hill
Relembrar ponte de Wheatstone