a utilização de livros paradidáticos para o ensino de probabilidade

A UTILIZAÇÃO DE LIVROS PARADIDÁTICOS PARA O ENSINO DE
PROBABILIDADE NO ENSINO FUNDAMENTAL
Valéria Ciabotti - UFTM1
Resumo
Os Parâmetros Curriculares Nacionais – PCN, Brasil (1997), preveem que no final do Ensino
Fundamental o aluno conclua essa etapa com a aprendizagem e domínio de conceitos básicos
sobre Probabilidade, quais sejam: (1) Relacionar o conceito de probabilidade com o de razão;
e (2) Resolver problemas que envolvam o cálculo de probabilidade de eventos simples.
Partindo desse pressuposto definiu-se como objetivo deste trabalho a busca de material
bibliográfico que pudesse subsidiar o ensino de conteúdos probabilísticos para os anos finais
do Ensino Fundamental através de livros paradidáticos. Partiu-se então para a busca de livros
paradidáticos que abordassem o conteúdo de Probabilidade para o Ensino Fundamental bem
como trabalhos didáticos que abordassem esta temática. Acreditamos ser necessário investigar
e buscar uma compreensão mais ampla e fundamentada sobre o uso de livros paradidáticos no
desenvolvimento da leitura e consequentemente nos conteúdos de Probabilidade que se ensina
no Ensino Fundamental. De acordo com Menezes e Santos (2002), os paradidáticos são livros
e materiais que, sem serem propriamente didáticos, são utilizados para este fim. Munakata
(1997), afirma que os paradidáticos têm características próprias, não seguem uma sequência
de conteúdos conforme preconiza o currículo oficial. Dada a importância do estudo dos
conteúdos básicos de probabilidade no mundo contemporâneo e com o propósito de adaptar
recursos como sugestão para os profissionais da educação no uso de paradidáticos, a pesquisa
mostra escassez de material no que se refere ao Ensino de Probabilidade nos anos finais do
Ensino Fundamental.
Palavras-chave: Ensino da Probabilidade. Paradidático. Estado da Arte. Ensino Fundamental.
Introdução
No final da década de 90, os conceitos básicos de Estatística e Probabilidade, antes
quase ignorados na Educação Básica, passaram a serem discutidos pela comunidade
educacional e acadêmica, tendo sido incorporados oficialmente à estrutura curricular da
disciplina de Matemática do Ensino Fundamental e Médio com a publicação dos Parâmetros
Curriculares Nacionais (PCN), Brasil (1997), no Bloco Tratamento da Informação, que
evidencia o ensino de Estatística, probabilidade e Análise Combinatória.
1
Ainda segundo os PCN, Brasil (1997), a sugestão é de que professores incentivem os
alunos a observar os fenômenos, conjeturar hipóteses, fazer levantamento de dados, tratá-los e
analisá-los do ponto de vista da investigação científica. Também estimulem a leitura e a
interpretação de gráficos, de tabelas e de medidas publicadas pelos diversos meios de
comunicação, a fim de que o aluno saiba posicionar-se de forma crítica diante dessas
informações e fornecer-lhes ferramentas para arguir e “desmantelar” informações porventura
falaciosas ou mal-intencionadas (LOPES et al, 2010).
Segundo Smole e Diniz (2001), a predominância do silêncio, no sentido de ausência
de comunicação, ainda é comum nas aulas de Matemática. O excesso de cálculos mecânicos,
a ênfase em procedimentos e a linguagem usada para ensinar Matemática são alguns dos
fatores que tornam a comunicação pouco frequente ou quase inexistente. Ainda afirmam que
as propostas que objetivem uma aprendizagem significativa em Matemática devem abordar
uma variedade de ideias, sejam numéricas, geométricas, relativas às medidas e às noções de
estatística, entre outras, de modo que sejam proporcionadas ao aluno diferentes formas de
perceber a realidade e o conhecimento matemático.
De acordo com os PCN, Brasil (1997), os objetivos das áreas disciplinares são
desenvolvidos e separados por ciclo e para cada um são propostos conteúdos e critérios de
avaliação que são agrupados em blocos temáticos, sendo que nessa pesquisa focou-se no
Ensino de Probabilidade nos anos finais do Ensino Fundamental, especificamente no nono
ano.
A partir da verificação dos conteúdos probabilísticos previstos nos Parâmetros
Curriculares Nacionais (PCN) (Brasil, 1997 e 1998) tem-se como objetivo a criação de
material paradidático para dar subsídios ao ensino de conteúdos probabilísticos para
professores de Matemática dos anos finais do Ensino Fundamental.
Diante disso questionou-se: como organizar o conteúdo? Qual recurso usar? Como e
onde abordar o tema? Como estabelecer relações com outros temas?
1. Referencial Teórico
As informações estatísticas sempre estiveram presentes na vida dos cidadãos e assim
como muitas pessoas confiam e utilizam para nortear suas decisões, outras olham, desconfiam
e/ou atacam sua verossimilhança (CAZORLA e CASTRO, 2008).
Em relação
à Probabilidade, consideram que esta pode promover a compreensão de grande parte dos
acontecimentos do cotidiano que são de natureza aleatória, possibilitando a identificação de
resultados possíveis desses acontecimentos. Destacam o acaso e a incerteza que se
manifestam intuitivamente, portanto cabendo à escola propor situações em que as crianças
possam realizar experimentos e fazer observações dos eventos.
Silva (2002) expressa que desde a sua origem, o conceito de probabilidades
desenvolveu-se em múltiplas perspectivas, quais sejam: (1) Concepção clássica ou laplaciana
(baseada na “Lei de Laplace”); (2) Concepção frequentista ou empírica (baseada na “Lei dos
Grandes Números” de Jacob Bernoulli); (3) Concepção subjetiva (baseada na crença ou
percepção pessoal); (4) Concepção axiomática ou formal (concepção atualmente vigente,
desenvolvida por Andrei Kolmogorov).
Batanero (2005) defende que os diferentes significados da Probabilidade devem ser
incluídos progressivamente a partir das ideias intuitivas dos alunos sobre acaso e incerteza, e
que o ensino não pode limitar-se a uma dessas perspectivas, pois elas estão ligadas
dialeticamente. Conclui que a Probabilidade deve ser vista como: (1) Uma razão entre o
número de possibilidades a favor do evento e o número de casos possível a partir dos dados
das frequências relativas; (2) O grau de crença pessoal; (3) Como um modelo matemático que
ajuda a compreender a realidade.
Menezes e Santos (2002) dizem que a importância dos livros paradidáticos nas
escolas aumentou principalmente no final da década de 90, a partir da Lei de Diretrizes e
Bases da Educação (LDB), que estabeleceu os PCN e orientou para a abordagem de temas
transversais relacionados ao desenvolvimento da cidadania. Dessa forma, abriu-se espaço para
o aumento da produção de obras para serem utilizadas em sala de aula, abordando temas
como ética, Pluralidade Cultural, Trabalho e Consumo, Saúde e Sexualidade.
Segundo Munakata (1997) o termo paradidático foi cunhado pelo saudoso professor
Anderson Fernandes Dias, diretor presidente da Editora Ática, no início da década de 70.
Continua afirmando que foi a Editora Ática que criou a primeira coleção de alcance no Brasil
destinada a apoiar, aprofundar e facilitar a maneira de apresentação dos conteúdos, muitas
vezes aridamente exposta no livro didático.
Atualmente é comum ouvirmos falar em livros paradidáticos, porém foi na década de
1970 que passaram a serem assim chamados (Ramos, 1987; Munakata, 1997; Dalcin, 2002),
devido à popularização do gênero.
Somente a partir de 1986 as primeiras coleções de paradidáticos de Matemática
começaram a surgir, como as coleções Vivendo a Matemática, da editora Scipione, e A
Descoberta da Matemática, da Ática (DALCIN, 2002).
Dalcin (2007) abordou em sua pesquisa acerca dos paradidáticos de Matemática, a
relação entre a simbologia matemática, as imagens e o texto escrito dentre as diversas
abordagens do conteúdo matemático.
Para entender a razão da criação do termo paradidático, Borelli (1996) apresenta o
sentido do termo paraliteratura, a partir da interpretação da formação da palavra com o prefixo
para denota tanto o significado de proximidade – ao lado de, ao longo de – quanto à
conotação de acessório, subsidiário, e, também, o sentindo de funcionamento desordenado ou
anormal.
Consideramos também a definição de Munakata (1997) ao afirmar que os livros
paradidáticos são livros que têm características próprias. Diferente dos livros didáticos, eles
não seguem uma seriação e nem uma sequência de conteúdos conforme preconiza o currículo
oficial. Geralmente, são adotados no processo de ensino e aprendizagem como material de
consulta do professor ou como fonte de pesquisa e de apoio às atividades do educando.
Segundo Machado apud Trevizan (2008), nos textos paradidáticos os temas
costumam ser apresentados de forma menos comprometido com o isolamento e a
fragmentação, possibilitando assim a relação com outras áreas de conhecimento.
2. Procedimentos Metodológicos
As pesquisas relacionadas aos anos finais do Ensino Fundamental, principalmente no
ensino de Probabilidade, representam uma grande contribuição para a área da Educação
Matemática, contudo, percebe-se que há, ainda, muitas lacunas a serem preenchidas. Tal
constatação provoca a necessidade de se estudar, pesquisar e produzir material didático para
apoiar o Ensino de Probabilidade nos anos finais do Ensino Fundamental.
Tendo em vista o tema e o problema de pesquisa levantados, o objetivo geral deste
trabalho é criar um material paradidático para dar subsídios ao ensino de conteúdos
probabilísticos para professores de Matemática dos anos finais do Ensino Fundamental.
Segundo Dalcin (2002) pode-se dividir os livros paradidáticos, segundo a sua
narrativa, em duas categorias: Narrativa ficcional – são livros que contém uma história de
ficção, na qual os elementos ou conteúdos abordados vão aparecendo; Abordagem pragmática
– são os livros que apresentam capítulos teóricos com atividades práticas sem um enredo
único.
Definiu-se que para a construção deste livro paradidático, a utilização da narrativa
ficcional, pois se acredita que contar uma estória trará maior motivação aos alunos em sua
leitura e utilização como elemento de fixação e aprendizagem dos conteúdos probabilísticos.
O material paradidático será produzido considerando os seguintes aspectos que
podem ser realizados concomitantemente e que foi expresso através de uma adaptação do
roteiro de avaliação de livros paradidáticos de Macedo et al. (2013): (1) Criar a estória que
será o fio condutor das ações a serem desenvolvidas;
(2) Utilizar os conteúdos
probabilísticos e matemáticos e os temas transversais (BRASIL, 1998); (3) Criar personagens;
(4) Criar as atividades utilizadas na abordagem do conteúdo probabilístico; (5) Considerar as
tendências do Ensino de Probabilidade;
(6) Considerar a diversidade de registros de
representações semióticas (DUVAL, 2011); (7) Oportunizar a participação do leitor na
construção do próprio conhecimento; (8) Diversificar os tipos de ilustrações utilizadas
(DALCIN, 2007); (9) Interagir com outras áreas do conhecimento (FAZENDA, 1994);
(10) Considerar a presença de elementos lúdicos (HUIZINGA, 1971); (11) Elaborar o texto;
(12) Possibilitar a utilização da obra em diversos momentos do estudo de determinado
conteúdo (na introdução, no decorrer, na finalização).
Os conteúdos probabilísticos considerados serão os listados no Conteúdo Básico
Comum (CBC) Matemática - do 6º ao 9º ano do Ensino Fundamental do Estado de Minas
Gerais, Minas Gerais (2008), no Eixo Temático IV – Tratamento da Informação –
Probabilidade – Conceitos Básicos de Probabilidade, e considerados como conteúdos a serem
ministrados no 9º ano, quais sejam: (1) Relacionar o conceito de probabilidade com o de
razão; (2) Resolver problemas que envolvam o cálculo de probabilidade de eventos simples.
Segundo os PCN, Brasil (1998) os conteúdos para o terceiro ciclo (6 e 7 anos)
referente a Probabilidade é a construção do espaço amostral e indicação da possibilidade de
sucesso de um evento pelo uso de uma razão (BRASIL, 1998, p. 74). Nos mesmos PCN, os
conteúdos para o quarto ciclo (8 e 9 anos) referente a Probabilidade são: (1) Construção do
espaço amostral utilizando o princípio multiplicativo e indicação da probabilidade de um
evento por meio de uma razão; (2) Elaboração de experimentos e simulações para estimar
probabilidades e verificar probabilidades previstas (BRASIL, 1998, p. 90).
3. Resultados
Levando em consideração o lançamento de um material em um determinado contexto
educacional, embasar-se em uma estória fictícia é uma estratégia pertinente para posterior
avaliação da credibilidade do mesmo. Ainda pensando na amostra da pesquisa serem alunos
do 9º ano do Ensino Fundamental, adolescentes e com o imaginário e a criatividade
ilimitáveis, pensou-se em abordar os conteúdos probabilísticos no formato de um livro
paradidático, visto que a escassez no Brasil foi detectado através da pesquisa realizada acerca
dos paradidáticos publicados com o enfoque no ensino de Probabilidade.
Após a definição do tema, pensou-se em como elaborar a estória principal do livro
abordando os tópicos definidos pelo CBC (Conteúdo Básico Comum, 2008), Matemática do
6º ao 9º ano do Ensino Fundamental e os PCN (Parâmetros Curriculares Nacionais, 1998),
Matemática 3º e 4º ciclos do Ensino Fundamental a saber: Conceito de Aleatoriedade e
Determinístico, Experimento Aleatório, Espaço Amostral, Evento e Definição de
Probabilidade, relacionando ainda Probabilidade com razão e porcentagem.
Para o desenvolvimento da estória principal do livro, pensou-se em abordar os
tópicos citados acima através de uma Olimpíada em que os alunos de várias escolas
competiriam, passando por várias etapas, sendo elas, municipal, estadual e finalmente
nacional, onde os personagens principais definidos por nós seriam os vencedores. O nome
fictício dado à Olimpíada foi 1ª Olimpíada Nacional de Probabilidade (ONP).
Para a escolha dos personagens, tomou-se bastante cautela, pensando em representar
vários grupos étnicos que compõem a sociedade brasileira, pois segundo Rocha (2006) é
indiscutível que os livros devam refletir as contribuições dos diversos grupos étnicos para a
formação da nação e cultura brasileira. Omitir essas contribuições, ou não reconhecê-las na
sua totalidade, é uma forma de discriminá-las.
Assim os personagens principais que compõe a estória são: um branco, um índio, um
japonês, um negro e um pardo. Segundo Blattes (2006) a Constituição da República, quando
adota como princípio a “igualdade de condições para o acesso e permanência na escola”,
prevê uma sociedade com escolas abertas a todos, em qualquer etapa ou modalidade, bem
como o acesso a níveis mais elevados do ensino. Partindo desse pressuposto um dos
personagens é cadeirante. A respeito do sexo dos personagens havia sido decidido que seriam
duas meninas e dois meninos, porque não havia sido incluído o personagem índio.
Após a inclusão do personagem índio, definiram-se então os personagens como três
meninas e dois meninos, utilizando como critério a pesquisa realizada pela PNAD (Pesquisa
Nacional de Amostra por Domicílio), divulgado em 20122 pelo IBGE (Instituto Brasileiro de
2
http://www.ibge.gov.br/home/estatistica/populacao/trabalhoerendimento/pnad2012/default_sintese.shtm
Geografia e Estatística) em que no Brasil tem mais mulheres do que homens, sendo que de
uma população de 196,9 milhões de habitantes 51,3% são mulheres e 48,7% são homens.
Foram definidos então os seguintes personagens principais: o personagem índio
(Kauê), o personagem pardo (Rafael), a personagem japonesa (Kaori), a personagem branca
(Gabriela), a personagem negra (Luíza) e a professora (Rita). Personagens que foram criados
e desenhados por um arte-finalista e que são apresentados na Figura 1.
Pensando nisso, criaram-se personagens fictícios que assumissem esses papéis até
como exemplo para os leitores (alunos, principalmente) dos objetivos dentro das salas de aula,
e do funcionamento da relação cíclica entre os envolvidos, nesses momentos de aprendizado.
Os nomes foram escolhidos aleatoriamente, seguindo o perfil das figuras criadas pelo artefinalista.
KAUÊ
GABRIELA
KAORI
LUIZA
RAFAEL
RITA (PROFESSORA)
Figura 1 – Imagem dos personagens criados para o livro paradidático.
À escola que os personagens seriam representantes deu-se o nome de “Escola Sete
Colinas”, Figura 2, essa escolha se deu pelo fato dos integrantes da pesquisa residir na cidade
de Uberaba-MG e também em homenageá-la.
Figura 2 – Logo da Escola Sete Colinas.
A pesquisa sobre a história da cidade de Uberaba relata que os primeiros habitantes
ergueram suas moradias na parte central da cidade, localizada numa depressão. O crescimento
da cidade e o relevo local fizeram com que a população ocupasse e povoasse as colinas, lugar
de maior altitude em relação à parte central da cidade. De acordo com Sampaio (1971), no
estudo topográfico de Uberaba publicado no ano de 1880, foram identificadas seis colinas.
Durante o século XX, Hildebrando Pontes, substituiu o termo Colinas por Altos e identificou
mais um Alto, o Fabrício (PONTES, 1978, p. 274). Assim a cidade de Uberaba era
referenciada como a Cidade das Sete Colinas. Com o crescimento da cidade e o surgimento de
novos bairros o título que recebia não compreendia a manutenção do mesmo conceito inicial
das colinas.
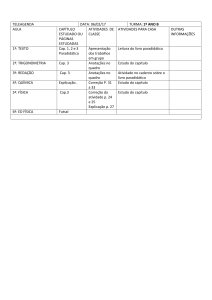
A Figura 3 mostra uma observação do Vale a partir de um Mirante muito conhecido
na cidade localizado em uma parte alta, o Mirante da Univerdecidade.
Fonte: Arquivo público de Uberaba 08 de março de 2013.
Figura 3 – Representação das Sete Colinas ou Sete Altos da cidade de Uberaba.
Em se tratando de ambiente escolar, Figura 4, não haveria melhor local para o
desenrolar da estória do paradidático e também sua utilização para fins de validação do
material proposto, não querendo inferir que não possa ser lido ou usado em outros lugares.
Além disso, aperfeiçoa o objetivo final trazendo a realidade do público leitor alvo para que se
familiarizem ainda mais com os temas propostos. Os professores são agentes principais na
promoção desse tipo de ambiente, onde utilizam como estratégia suas lideranças para que se
tenha como produto final a compreensão total de tudo que pretendem transmitir.
Figura 4 – Ambiente escolar e os personagens.
Segundo Moreira (2007), “o ambiente de aprendizagem escolar é um lugar
previamente organizado para promover oportunidades de aprendizagem e que se constitui de
forma única na medida em que é socialmente construído por alunos e professores a partir das
interações que estabelecem entre si e com as demais fontes materiais e simbólicas do
ambiente”. MOREIRA (2007).
O livro foi dividido em quatro capítulos onde em cada um será realizada uma das
etapas da Olimpíada. Dessa forma, em cada capítulo, os conteúdos probabilísticos a serem
abordados serão utilizados jogos onde os personagens irão participar para se tornarem
campeões nacionais.
De acordo com Cabral (2006), os jogos vêm ganhando espaço nas escolas numa
tentativa de trazer o lúdico para a sala de aula. Acreditamos que os jogos podem ser atividades
excelentes para a introdução de conceitos do campo da Probabilidade. Vários tipos deles
ajudam a compreender a diferença entre situações aleatórias e determinísticas ou a diferenciar
possibilidades de probabilidade (BRASIL, 2010).
Dessa forma, decidiu-se utilizar jogos para se trabalhar os conteúdos probabilísticos,
inserindo esses jogos como etapas das Olimpíadas em que os personagens iriam participar
para se tornarem campeões nacionais.
Foi inserido também atividades como jogos e divertimentos onde os alunos que
utilizarão o paradidático deverão fazer para ajudar os personagens principais a vencer a
Olimpíada, além de caça-palavras e cruzadinhas como entretenimento.
Esses jogos serão aplicados para testar a eficácia e serão introduzidos na estória tendo
como função a de fixar o conteúdo já inserido pela professora regente das cinco turmas de 9º
anos.
Assim no Capítulo 1, é apresentado o jogo a ser utilizado na 1ª etapa que recebe o
nome de “Jogo do Rapa”. É um dos jogos mais populares de Portugal, onde traz diversas
possibilidades de trabalhar conceitos probabilísticos.
No Capítulo 2, é utilizado o jogo “Mini Bozó”, que é uma simplificação do “Jogo
Bozó”, jogo bastante popular no estado do Mato Grosso do Sul, Brasil.
No Capítulo 3, é apresentado o jogo “Batalha no Trânsito” que foi adaptado do jogo
“Batalha Naval”, um jogo muito conhecido.
E o jogo que compõe a etapa final da Olimpíada, Capítulo 4, se chama “Bingo das
Probabilidades”, jogo criado pelos pesquisadores.
Direcionamos também as atividades para a proposta da elaboração do paradidático
nas concepções: clássica e frequentista, por concordar com autores e pesquisadores que
defendem a ideia do uso desse recurso concomitantemente nas situações do Ensino de
Probabilidade.
Entende-se como Probabilidade Clássica a razão entre o número de resultados
favoráveis ao evento que se quer estudar e o número total de resultados possíveis (o qual é
denominado de espaço amostral) do experimento aleatório, tomando que cada resultado
possível de um determinado Experimento Aleatório seja igualmente provável de ocorrer.
(CABRAL, 2009; BATANERO, 1999).
Coutinho (1994, p. 09) defende a visão frequentista de probabilidade que parece “[...]
mais adequada a um primeiro contato com as probabilidades, pois pode utilizar experimentos
ligados à realidade dos alunos, uma vez que não precisa estar limitado à hipótese de
equiprobabilidade”. A presença da probabilidade frequentista no ensino se justifica por fazer
parte de nosso cotidiano, pois estamos sempre cercados de informações presentes em jornais,
revistas, televisão, internet e noticiários onde a maioria dos dados probabilísticos é calculada
por meio dessa probabilidade.
A importância de se trabalhar com os diversos significados da probabilidade, tais
como a Probabilidade Clássica (ou Laplaciana), Frequentista, Geométrica e Condicional, de
acordo com o grau de instrução dos alunos vem sendo estudado e discutido por alguns
pesquisadores, destacando-se os estudos de Ortiz (2002); Stadelmanns (2003); Anway e
Bennett (2004); Batanero (2005); Viali e Oliveira (2009); e Cabral e Traldi (2010).
Batanero (2005) defende que os diferentes significados da Probabilidade devem ser
incluídos progressivamente a partir das ideias intuitivas dos alunos sobre acaso e
probabilidade, e que o ensino não pode limitar-se a uma dessas perspectivas, pois elas estão
ligadas dialeticamente.
Os trabalhos de Silva (2002) e Cabral e Traldi (2010) propõem a integração dos
conceitos Frequentista e Clássico com o intuito de tornar a aprendizagem significativa e
abrangente.
Considerações Finais
Por se tratar de parte de uma pesquisa que ainda se encontra em seu processo de
desenvolvimento, as análises ainda estão em fase de constituição, visto que a utilização do
livro paradidático ainda não foi efetivado, mesmo assim, já se percebe que, o caminho da
utilização de livros paradidáticos na contribuição na formação de significados dos conteúdos
probabilísticos nas relações é revelador. O livro paradidático, com um aspecto mais informal e
descontraído, orienta, auxilia e forma o cidadão na compreensão do mundo.
Pensando assim, a ideia de elaborar um livro paradidático utilizando conhecimentos
probabilísticos suscitou a busca tanto de conhecer a particularidade que esse tipo de livro traz
como também a exploração do conteúdo sobre Probabilidade na Educação Básica.
Na construção do livro paradidático, percebemos a importância e a função desse
recurso que segundo Trevizan (2008), motiva, exemplifica e aprofunda um conteúdo
específico.
Referências
ANWAY, D.; BENNETT, E. Common Misperceptions in Probability among Students in an
Elementary Statistics Class. In: Proceedings of Conference on Assessment in Statistics,
Lawrence
University,
1-4
aug.
2004.
(p.
1-13).
Disponível
em:
<http://www.rossmanchance.com/artist/proceedings/AnwayBennett.pdf>. Acesso em: 18 jul.
2015.
BATANERO, M. C. Didáctica de la Probabilidad y Estadística. Granada: Departamento de
Didáctica de la Matemática,1999.
BATANERO, C. Significados de La Probabilidad em la Educación Secundaria. RELIME:
Revista Latinoamericana de Investigacion en Matemática Educativa, v. 8, n. 3, p. 247-263,
nov. 2005.
BLATTES. R. L. Direito à Educação: subsídios para a gestão dos sistemas educacionais:
orientações gerais e marcos legais. 2. ed. Brasília: MEC, SEESP, 2006. (p. 343).
BORELLI, S. H. S. Ação, suspense, emoção: Literatura e cultura de massa no Brasil. São
Paulo: EDUC/Estação Liberdade, 1996.
BRASIL. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais:
Matemática. Brasília: MEC/SEF, 1997.
BRASIL. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais:
Matemática. Brasília: MEC/SEF, 1998.
BRASIL. Coleção explorando o Ensino. Brasília: Ministério da Educação, Secretaria de
Educação Básica, 2010.
CABRAL, M. A. A utilização de jogos no ensino de matemática. 2006. Monografia (Trabalho
de Conclusão de Curso em Matemática) – Universidade Federal de Santa Catarina, Santa
Catarina, Brasil, 2006.
CABRAL, R. S. J. Abordagem das noções iniciais de probabilidade em uma perspectiva
construtivista. 2009. 102 f. Dissertação (Mestrado Profissional em Ensino de Matemática) –
Pontifícia Universidade Católica de São Paulo, São Paulo, 2009.
CABRAL JR, R. S.; TRALDI J, A. Abordagem das Noções Iniciais de Probabilidade em uma
Perspectiva Construtivista. In: Anais do X Encontro Nacional de Educação Matemática,
Salvador, 2010. (p. 1-12).
CAZORLA, I. M.; CASTRO, F. C. de. O papel da estatística na leitura do mundo: o
letramento estatístico. Humanit. Sci., Appl. Soc. Sci., Linguist., Lett. Arts, v. 16, n. 1, p. 45-53,
2008.
COUTINHO, C. Q. S. Introdução ao Conceito de Probabilidade por uma Visão Frequentista.
1994. 151 f. Dissertação (Mestrado em Matemática) – Pontifícia Universidade Católica de
São Paulo, São Paulo, Brasil, 1994.
DALCIN, A. Um olhar sobre o paradidático de matemática. 2002. 222 f. Dissertação
(Mestrado em Educação Matemática) UNICAMP, Faculdade de Educação, Campinas, 2002.
DALCIN, A. Um olhar sobre o paradidático de matemática. Zetetiké. Unicamp, v. 15, n. 27,
p. 25-35, 2007.
DUVAL, R. Ver e ensinar a matemática de outra forma: Entrar no modo matemático de
pensar: os registros de representações semióticas. 1.ed. São Paulo: PROEM, 2011.
FAZENDA, I. C. A. Interdisciplinaridade: história, teoria e pesquisa. Campinas: Papirus,
1994.
HUIZINGA, J. Homo ludens: o jogo como elemento da cultura. São Paulo: Perspectiva, 1971.
LOPES, C.E.; COUTINHO, C.Q.; ALMOULOUD, S. Estudos e reflexões em Educação
Estatística. 1. ed. Campinas : Ed. Mercado de Letras, 2010.
MACEDO. E. S. de; CARDOSO, M. D. C. L.; PONTES, M. O.; SILVA, M. P. F.
Paradidáticos nas aulas de matemática. In: Actas del VII CIBEM – Uruguai, 2013. (p. 73127319).
MENEZES, E. T. de.; SANTOS, T. H. dos. Paradidáticos (verbete). Dicionário Interativo da
Educação Brasileira - EducaBrasil. São Paulo: Midiamix Editora, 2002. Disponível em:
<http://www.educabrasil.com.br/eb/dic/dicionario.asp?id=143>. Acesso em: 14. Jun. 2014.
MINAS GERAIS. Secretaria de Educação. Conteúdo Básico Comum. Belo Horizonte: SEEMG, 2008a.
MOREIRA, A. F. Ambientes de aprendizagem no ensino de ciência e tecnologia. Belo
Horizonte. 2007. In: BRAGANÇA, B.; FERREIRA, L. A. G.; PONTELO; I, Práticas
educativas e ambientes de aprendizagens escolar: relato de três experiências. 1º Seminário
Nacional de Educação Profissional e Tecnológica. Belo Horizonte, 2008.
MUNAKATA, K. Produzindo livros didáticos e paradidáticos. Tese (Doutorado em História
e Filosofia da Educação). São Paulo: PUC, 1997.
ORTIZ, J. J. La probabilidad en los libros de texto. Grupo de Investigación en Educación
Estadística. Departamento de Didáctica de la Matemática. Universidad de Granada, 2002.
PONTES, H. História de Uberaba e a Civilização do Brasil Central. Uberaba: Academia de
Letras do Triângulo Mineiro, 1978.
RAMOS, M. C. M. O paradidático, esse rendoso desconhecido. 1987. 214 f. Tese (Doutorado
em Educação) - Faculdade de Filosofia, Letras e Ciências Humanas, Universidade de São
Paulo, São Paulo, 1987.
ROCHA, L. C. da. As relações étnico-raciais, a cultura afro-brasileira e o projeto políticopedagógico. Salto para o futuro, currículo, relações sociais e cultura afro-brasileira, Boletim
20, Ministério da Educação, 2006.
SAMPAIO, A. B. Uberaba: história, fatos e homens. Academia de Letras do Triângulo
Mineiro, Bolsa de Publicações do Município de Uberaba, v. 1, p. 47, 1971.
SILVA, I. A. Probabilidades: a visão laplaciana e a visão frequentista na introdução do
conceito. São Paulo, 2002. 174 f. Dissertação (Mestrado em Educação Matemática). Centro
de Ciências Exatas e Tecnologia, Pontifícia Universidade Católica de São Paulo, 2002.
SMOLE, K. S.; DINIZ, M. I. Ler, escrever e resolver problemas: habilidades básicas para
aprender Matemática. Porto Alegre: Artmed Editora, 2001.
STADELMANN, D. Les conceptions de la probabilité: Comparaison des différentes
approches. Travail de séminaire. Université de Fribourg / Universität Freiburg Faculté des
sciences économiques et sociales, Département d‟économie quantitative, 2003.
TREVIZAN, W. A. O uso do livro paradidático no ensino de matemática, 2008. Disponível
em: <www.usp.br/siicusp/Resumos/16Siicusp/807.pdf>. Acesso em: 15. Jun. 2014.
VIALI, L.; OLIVEIRA, P. I. F. Uma Análise de Conteúdos de Probabilidade em Livros
Didáticos do Ensino Médio. In: Anais do IV Seminário Internacional de Pesquisa em
Educação Matemática, Brasília, 2009.