CONCEITOS BÁSICOS EM ESTATÍSTICA

Tópico 6
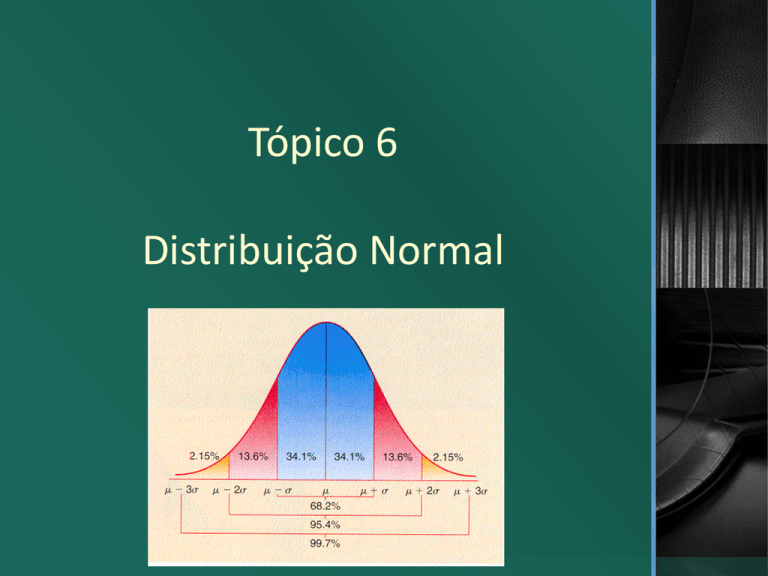
Distribuição Normal
Distribuição Normal
 Existe uma importante diferença entre dados
que são “normalmente” distribuídos e a curva
normal em si
Distribuição Normal
 Muitas variáveis apresentam distribuição onde
os valores centrais são mais frequentes e os
valores extremos são mais raros
 Exemplo: Tempo de 600 corredores brasileiros
nos 400 m livre do atletismo
 WR = 43.18s
Distribuição Normal
 Frequência relativa
Tempo (s)
fr
46--47,99
48--49,99
50--51,99
52--53,99
54--55,99
56--57,99
58--59,99
0,01
0,06
0,24
0,38
0,23
0,07
0,01
Distribuição Normal
 Frequência relativa
Distribuição Normal
 Distribuições nem sempre tão certinhas
Distribuição Normal
 Distribuições nem sempre tão certinhas
Curva Normal
 Curva normal é uma abstração matemática
com uma equação específica que a define
fr
Curva Normal
 Características da curva normal
S
U
M
A
 A proporção da área abaixo da curva relativa a uma
particular amplitude de valores sobre o eixo
horizontal é sempre a mesma**
Curva Normal
 ** Considere uma curva normal caracterizada
por:
 μ = 100
 σ = 20
 O que se pode afirmar?


Curva Normal
 Mesma média, desvio padrão diferente
Curva Normal
 Mesmo desvio padrão, médias diferentes
Curva Normal
 Curva normal é, de fato, uma família de curvas
 As médias podem variar
 Os desvios padrão podem variar
 A forma da curva depende do seu desvio padrão
 Mais achatada
 Mais esticada
 MAS, a área abaixo de todas as curvas normais é
sempre distribuída da mesma maneira
Curva Normal
 O que
significa “a
área abaixo
de todas as
curvas
normais é
sempre
distribuída
da mesma
maneira”?
Curva Normal
 O que
significa “a
área abaixo
de todas as
curvas
normais é
sempre
distribuída
da mesma
maneira”?
Curva Normal
 O que
significa “a
área abaixo
de todas as
curvas
normais é
sempre
distribuída
da mesma
maneira”?
Curva Normal
 O que
significa “a
área abaixo
de todas as
curvas
normais é
sempre
distribuída
da mesma
maneira”?
Curva Normal
 Qual a vantagem de conhecer a área abaixo da
curva normal?
 Conhecer chances, probabilidade de um evento
ocorrer
 Você pode responder perguntas do tipo: Qual a
probabilidade de encontrar sujeitos que estão acima
ou abaixo determinado escore?
 Para tanto, você precisa converter seus dados brutos
em dados padronizados
Curva Normal
 O que significa “converter seus dados brutos em
dados padronizados”?
Curva Normal Padronizada
 A curva normal padronizada tem:
 Média = 0
 Desvio padrão =1
 As áreas situadas abaixo desta curva são
padronizadas e tabeladas
 Entre a média (zero) e um valor qualquer de z
(positivo ou negativo)
Usando a Curva Normal
 Exemplo 1 (adaptado de Callegari-Jacques, 2003)
 Um treinador deseja selecionar dentre os 240 jovens
que estão prestando o serviço militar em um quartel,
aqueles mais altos para montar um time de basquete.
 Sabe-se que a estatura dos recrutas tem uma
distribuição normal, com média de 175 cm e desvio
padrão de 6cm.
 Assim, o treinador decide selecionar apenas aqueles
que tenham uma estatura mínima de 180 cm.
 Quantos jovens este treinador vai encontrar no
quartel com este perfil?
Usando a Curva Normal
 Exemplo 1 – Encontrando a área abaixo da curva normal que está
acima de um valor conhecido
 Passo 1 – Desenhe a curva normal
fr
175
0
180
?
Est (cm)
z
Usando a Curva Normal
 Exemplo 1 – Encontrando a área abaixo da curva normal que estão
acima de um valor conhecido
 Passo 2 – Calcule o valor padronizado (z) para o valor
de interesse da sua variável (x)
Usando a Curva Normal
 Exemplo 1 – Encontrando a área abaixo da curva normal que estão
acima de um valor conhecido
O que significa
este 0,83?
fr
175
0
180
0,83
Est (cm)
z
Usando a Curva Normal
 Exemplo 1 – Encontrando a área abaixo da curva normal que está
acima de um valor conhecido
 Passo 3 – Consulte a tabela de Distribuição Normal (z)
para saber a área entre μ e z
fr
0
0,83
Est (cm)
z
Usando a Curva Normal
 Exemplo 1 – Encontrando a área abaixo da curva normal que está
acima de um valor conhecido
 Passo 3 – Consulte a tabela de Distribuição Normal (z)
para saber a área entre μ e z
Área entre 0 e 0,83 = 0,2967
Usando a Curva Normal
 Exemplo 1 – Encontrando a área abaixo da curva normal que está
acima de um valor conhecido
 Passo 4 – Calcule a área que está além de z
fr
Est
z (cm)
Área além de z (0,83) = 0,5 - 0,2967 = 0,2033
 20,33% dos recrutas tem
Usando a Curva Normal
 Exemplo 1 – Encontrando a área abaixo da curva normal que está
acima de um valor conhecido
 Passo 5 – Responda à pergunta inicial – Quantos
recrutas têm estatura igual ou superior a 180 cm?
20,33% de 240 ⟹ 0,2033 × 240 = 48,79
 Entre
Usando a Curva Normal
 E se o treinador resolvesse aumentar a estatura mínima
para 190cm. Quantos recrutas ele conseguiria?
fr
z = 2,5
0,62% da área
1,488
175
0
190
Est (cm)
z
?
Usando a Curva Normal
 Exemplo 2 – Encontrando a área abaixo da curva
normal que está abaixo de um valor conhecido
 Você é um técnico de atletismo de uma pequena cidade do
interior, que está procurando por velocistas.
 Você fez um teste com 1500 estudantes do ensino
fundamental. Pediu para que eles corressem 40m e marcou
seus tempos.
 A distribuição dos tempos obtidos se aproxima de uma
distribuição normal.
 Agora você quer selecionar para sua equipe apenas aqueles
que estão 2 desvios padrão abaixo da média. Quantas vagas
precisa ter?
Usando a Curva Normal
 Exemplo 2 – Encontrando a área abaixo da curva normal que está
abaixo de um valor conhecido
fr
t (s)
-2
0
z
Usando a Curva Normal
 Exemplo 2 – Encontrando a área abaixo da curva normal que
está abaixo de um valor conhecido
 Como a curva normal é simétrica, o procedimento é o
mesmo do exemplo 1. Basta repetir os passos!
 Algumas tabelas de distribuição normal já trazem o valor de z
além de determinado desvio padrão
 No caso de z = 2, esta área é de 0,0228
 Resposta ao nosso técnico:
Estratégia Z – O milagre de descobrir campeões
 Celafiscs – São Caetano, décadas de 80/90
 Testes motores para predizer talentos para
determinados esportes (maioria, coletivos)
 Trunfo: tinham dados populacionais (apesar de ser de
uma única cidade)
Referências
 ANDERSON, D.; SWEENEY, D.; WILLIAMS, T. (2003).
Estatística Aplicada à Administração e Economia. 2nd ed.
São Paiulo: Pioneira Thomson Learning.
 KING, B. M.; MINIUM, E. M. (2003). Statistical Reasoning in
Psychology and Education . 4th ed. New Jersey: John Wiley
& Sons, Inc.
 CALLEGARI-JACQUES, S. M. (2003). Bioestatística:
princípios e aplicações. Porto Alegre: Artmed.
 KAZMIER, L. J. (2004). Estatística aplicada à economia e
administração. São Paulo: Pearson Makron.
Sugestão de Leitura
 Capítulos 4 de:
 CALLEGARI-JACQUES, S. M. (2003). Bioestatística: princípios
e aplicações. Porto Alegre: Artmed.
Distribuição Normal – Tabela z