Rasterização de linhas e polígonos Algoritmos de rasterização de

Computação Gráfica Interativa - Gattass
2000.03.25
Rasterização de linhas e
polígonos
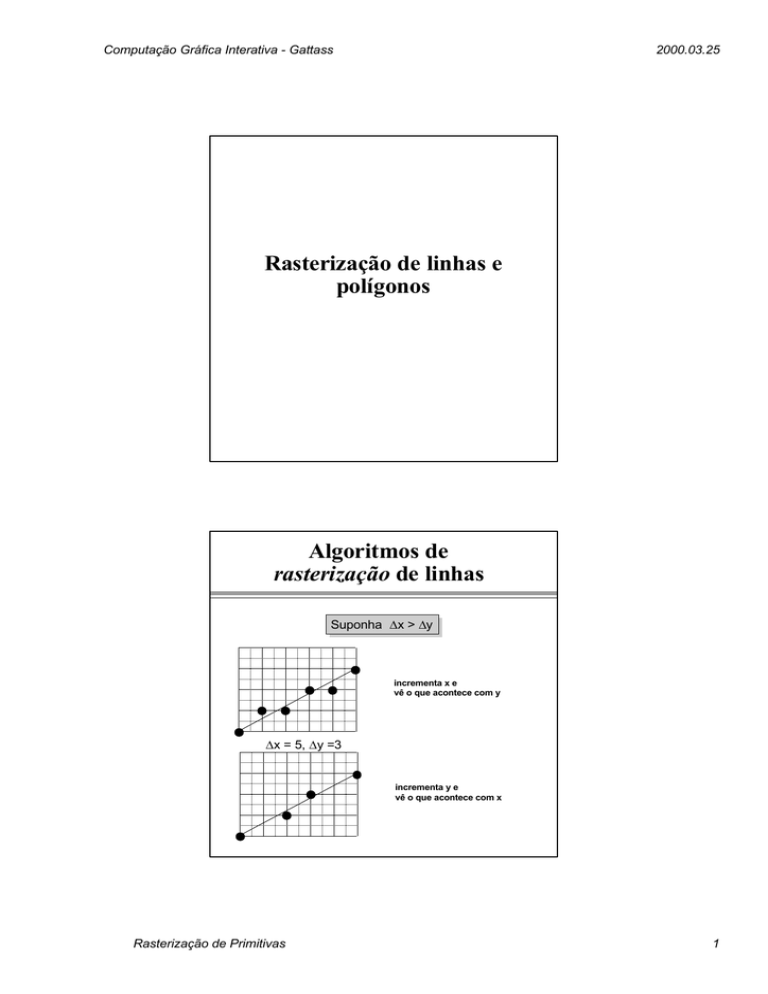
Algoritmos de
rasterização de linhas
Suponha
Suponha ∆x
∆x>>∆y
∆y
incrementa x e
vê o que acontece com y
∆x = 5, ∆y =3
incrementa y e
vê o que acontece com x
Rasterização de Primitivas
1
Computação Gráfica Interativa - Gattass
2000.03.25
Algoritmo simples de linha
(no primeiro octante)
yi = m xi + b
onde:
m = ∆y/∆x
b = y1 - m x1
void Line(int x1, int y1, int x2, int y2, int color)
{
float m = (y2-y1)/(x2-x1);
float b = y1 - m*x1;
float y;
SetPixel(x1,y1, color);
y = y1;
while( x1 < x2 )
{
x1++;
y = m*x1 + b;
SetPixel(x1,ROUND(y), color);
}
}
Algoritmo de linha
incremental
Se
xi+1 = xi + 1
então
yi+1 = yi + ∆y/∆x
void LineDDA(int x1, int y1, int x2, int y2, int color)
{
float y;
float m = (y2-y1)/(x2-x1);
SetPixel(x1,y1, c);
y = y1;
while( x1 < x2 )
{
x1++;
y += m;
SetPixel(x1,ROUND(y), c);
}
}
Rasterização de Primitivas
2
Computação Gráfica Interativa - Gattass
2000.03.25
Algoritmo de linha
baseado no erro
void BresLine0(int x1, int y1, int x2, int y2, int c)
{
int Dx = x2 - x2;
int Dy = y2 - y1;
float e= -0.5;
SetPixel(x1, y1, c);
erro de manter y
- 0.5 0.5
while( x1 < x2 )
{
x1++; e+=Dy/Dx;
x
if (e>=0) {
y1++ ; e -= 1;
}
- 0.5 0.5
e = erro - 0.5
x
SetPixel(x1, y1, c);
}
}
Algoritmo de Bresenham
ei = 2*Dx*e
void
voidBresLine0(int
BresLine0(intx1,
x1,int
inty1,
y1,
int
int x2,
x2,int
inty2,
y2,int
intc)c)
{{
int
int Dx
Dx==x2
x2- -x1;
x1;
int
int Dy
Dy==y2
y2- -y1;
y1;
float
e=
-0.5;
float e= -0.5;
void
voidBresLine1(int
BresLine1(intx1,
x1,int
inty1,
y1,
int
int x2,
x2,int
inty2,
y2,int
intc)c)
{{
int
int Dx
Dx==x2
x2- -x1;
x1;
int
int Dy
Dy==y2
y2- -y1;
y1;
int
ei
=
-Dx;
int ei = -Dx;
SetPixel(x1,
SetPixel(x1,y1,
y1,c);
c);
SetPixel(x1,
SetPixel(x1,y1,
y1,c);
c);
while(
while(x1
x1<<x2
x2) )
{{
x1++;
x1++; e+=Dy/Dx;
e+=Dy/Dx;
while(
while(x1
x1<<x2
x2) )
{{
x1++;
x1++; eiei+=
+=2*Dy;
2*Dy;
}}
ifif(e>=0)
(e>=0){{
y1++
y1++; ; ee-=
-=1;1;
}}
ifif(ei>=0)
(ei>=0){{
y1++
y1++; ; eiei-=
-=2*Dx;
2*Dx;
}}
SetPixel(x1,
SetPixel(x1,y1,
y1,c);
c);
}}
SetPixel(x1,
SetPixel(x1,y1,
y1,c);
c);
}}
}}
válidos somente quando Dx>Dy, x2 > x1 e y2 > y1
Rasterização de Primitivas
3
Computação Gráfica Interativa - Gattass
2000.03.25
Equação implícita da reta
y
y=
F ( x, y) < 0
dy
x+B
dx
y2
F ( x, y) > 0
y1
n = (dy
x1
− dx )
x
x2
F ( x , y ) = dy. x − dx. y + B. dx = 0
F ( x , y ) = a . x + b. y + c
NE
yp+ 1/2
M
yp
E
xp
xp+1
xp+2
Algoritmo do ponto médio
- variável de decisão MNE
yp+3/2
NE
yp+1/2
M
yp
ME
 > 0 → escolha NE
F( M) = 
 ≤ 0 → escolha E
E
xp
xp+1
d = F ( x p + 1, y p +
xp+2
1
2)
d new = F ( x p + 2 , y p +
1
E
= a ( x p + 1) + b ( y p +
2)
1
= a (x p + 2) + b( y p +
d new = d old + a
d new = F ( x p + 2 , y p +
NE
Rasterização de Primitivas
3
2)
1
+c
2)
+c
∆E = a
= a (x p + 2) + b( y p +
d n e w = d old + a + b
2)
3
2)
+c
∆ NE = a + b
4
Computação Gráfica Interativa - Gattass
2000.03.25
Algoritimo do ponto médio
- redução para inteiros d start = F ( x 0 + 1, y 0 +
1
2)
= a ( x 0 + 1) + b ( y 0 +
1
2)
+c
d start = F ( x0 , y 0 ) + a + b / 2 = a + b / 2
∆E = a
∆ NE = a + b
d = 2. F ( x , y )
d start = 2. a + b
∆ E = 2a
∆ NE = 2(a + b )
Algoritimo do ponto médio
- código C void MidpointLine(int x0, int y0, int x1, int y1,
{
int dx = x1-x0;
int dy = y1-y0;
int d=2*dy-dx;
/* Valor inicial da var.
int incrE = 2*dy;
/* incremento p/ mover
int incrNE = 2*(dy-dx); /* incremento p/ mover
int x=x0;
int y=y0;
Pixel(x,y,fgcolor); /* Primeiro pixel */
int color)
decisao */
E */
NE */
while (x<xl) {
if (d<=0) { /* Escolha E */
d+=incrE;
x++;
} else {
/* Escolha NE */
d+=incrNE;
x++;
y++;
}
Pixel(x,y,color);
} /* while */
} /* MidpointLine */
Rasterização de Primitivas
5
Computação Gráfica Interativa - Gattass
2000.03.25
Estilos de linha
void MidpointLine(int x0, int y0, int x1, int y1,
{
int dx = x1-x0;
int dy = y1-y0;
int d=2*dy-dx;
/* Valor inicial da var.
int incrE = 2*dy;
/* incremento p/ mover
int incrNE = 2*(dy-dx); /* incremento p/ mover
int x=x0; int y=y0;
int color)
decisao */
E */
NE */
int style[8]={1,1,0,0,1,1,0,0}; int k=1;
Pixel(x,y,fgcolor)}
while (x<xl) {
if (d<=0) { /* Escolha E */
d+=incrE;
x++;
} else {
/* Escolha NE */
d+=incrNE;
x++;
y++;
}
if (style[(++k)%8]) Pixel(x,y,color);
} /* while */
} /* MidpointLine */
Rasterização de Retas
-caso geraly
1
2
2
y
1
x
orientação
x
outros quadrantes
Rasterização de Primitivas
6
Computação Gráfica Interativa - Gattass
2000.03.25
Rasterização de Cônicas
y


∇F = 


F(x,y) = 0
∂F
∂x
∂F
∂y





x
450
y
simetrias do círculo:
cada ponto calculado
define 8 pixels
x
Rasterização de Cônicas
y
y=raio;
for (x=0; x< y; x++) {
if F(M)<0
escolha E
else
escolha SE
Pixel (E ou SE)
pinte os simétricos
}
x
E
ME
M
SE
Rasterização de Primitivas
F(x,y) = 0
MSE
7
Computação Gráfica Interativa - Gattass
2000.03.25
Preenchimento de polígonos
dados:
dados:
{x
,
x
{x00, x11, ,xx22, ,xx3,3,xx4}4}
{y
{y00, ,yy11, ,yy22, ,yy3,3,yy4}4}
y
ymax
1
4
i1
ys
i0
i4
i3
acha
ey
achayymax
max e ymin
min
0
ymin
Para
∈∈ [y[ymax , ,yymin]]
Paracada
cadays∈
ys∈
max
min
Para
Paracada
cadaaresta
aresta
2
3
0
xi1
xi0
xi4
xi3
vx=
vx={x
{xi1i1, ,xxi0i0, ,xxi4i4, ,xxi3i3}}
calcula
calculaas
asinterseções
interseções
x
ordena
ordenainterseções
interseções
desenha
desenhalinhas
linhashorizontais
horizontais
Preenchimento de polígonos
(scan passando por vértices)
y
1
ys
i0
0
i4
5 i3
i1 i2
3
2
4
0
x
inclui
incluivértices:
vértices:
i0-i1,
i0-i1,i2-i3,
i2-i3,i4-?
i4-?
não
nãoinclui
incluivértices:
vértices:
i0-?
i0-?
y
y
1
ys
i0
i1 i2
3
0
1
i4
i3 5
ys
3
L
2
4
4
Rasterização de Primitivas
5
L
2
0
0
i0
x
0
x
8
Computação Gráfica Interativa - Gattass
2000.03.25
Interseção nos vértices
só
sóinclui
incluivértices
vérticesde
demenor
menory:y: ou
i0-i4
J
i0-i4
só
sóinclui
incluivértices
vérticesde
demaior
maiory:y:
J
i0-i1,
i0-i1,i2-i3
i2-i3
reta
retahorizontal
horizontalnão
nãoproduz
produzinterseção
interseção
Algoritmo de Fill
void FillPolygon (int np, int *x, int *y)
{
/* declarações */
. . .
/* calcula y max e min dos vértices*/
. . .
for(ys=ymim; ys<=ymax; ys--)
/* para cada linha de scan */
{
num_inters = 0;
for(i=0; i<np; i++)
/* para cada aresta */
{
yi = y[i];
yf = y[(i+1)%np];
if (yi!=yf && ys >= MIN(yi,yf) && ys < MAX(yi,yf) )
{
vxs[num_inters] = x[i] +
(ys-yi)*(x[(i+1)%np]-x[i])/(yf-yi);
num_inters++;
}
}
ordena(vxs,0,num_inters-1);
for (i=0;i<num_inters;i+=2)
if (vxs[i]+1 <= vxs[i+1])
/* ordena as interseções */
ScanLine(vxs[i],vxs[i+1],ys);
}
Rasterização de Primitivas
9
Computação Gráfica Interativa - Gattass
2000.03.25
Otimizações do algoritmo de fill
y
ymax
xx==x+dx
x+dx
ys+1
ys
dy = 1
ymin
x0
Lista de Arestas
x1
x (ou z)
dx = (x1-x0)/(ymax-ymin)
struct edge
{
int
y_max;
int
y_min;
float
xs;
/* maior y da aresta */
/* menor y da aresta */
/* x correspondente a ys */
/* (no início é o correspondente a y_max) */
float delta_xs; /* incremento de xs entre duas linhas de scan */
};
Algoritmo de Fill de Polígonos
(Parte 1-Alocação de Memória)
#define Max(a,b)
#define Min(a,b)
(((a) > (b)) ? (a) : (b))
(((a) < (b)) ? (a) : (b))
void fill (int np, int *x, int *y)
{
static struct edge *aresta=NULL;
/* vetor de arestas */
static int *vxs=NULL;
/* vetor de interseções */
static int old_np=0;
/* número de pontos da última chamada */
int
int
int
int
int
ymax, ymin;
num_inters;
num_arestas;
ys;
i;
/*
/*
/*
/*
limites do polígono */
num. de interseções */
num. de arestas */
ordenada da reta de scan */
/* realoca os vetores de arestas e de interseções */
if (np > old_np)
{
old_np=np;
if (vxs) free (vxs);
if (aresta) free (aresta);
vxs=(int *) malloc ((np-1)*sizeof(int)); /* max num. De inters.*/
aresta=(struct edge *) malloc (np*sizeof(struct edge));
}
/* CONTINUA NA PARTE 2 */
Rasterização de Primitivas
10
Computação Gráfica Interativa - Gattass
2000.03.25
Algoritmo de Fill de Polígonos
(Parte 2-Lista de Arestas)
/* PARTE 1*/
/* calcula y max e min e monta o vetor de arestas */
ymax = y[0];
ymin = y[0];
num_arestas = 0;
for(i=0;i<np;i++)
{
int i1=(i+1)%np;
if (y[i] != y[i1])
{
aresta[num_arestas].y_max = Max(y[i],y[i1]);
aresta[num_arestas].y_min = Min(y[i],y[i1]);
aresta[num_arestas].delta = ((float)(x[i1]-x[i])/
(float)(y[i1]-y[i]));
if (aresta[num_arestas].y_mim == y[i])
aresta[num_arestas].xs = x[i];
else
aresta[num_arestas].xa = x[i1];
if (aresta[num_arestas].y_max > ymax)
ymax = aresta[num_arestas].y_max;
if (aresta[num_arestas].y_min < ymin)
ymin = aresta[num_arestas].y_min;
num_arestas++;
}
}
/* CONTINUA NA PARTE 3 */
Algoritmo de Fill de Polígonos
(Parte 3-Varredura)
/* PARTES 1 E 2 */
for(ys=ymin; ys<ymax; ys++) /* para cada linha de scan */
{
num_inters = 0;
for(i=0; i<num_arestas; i++)
{
if (aresta[i].y_max < ys){
/* retira da lista de arestas */
aresta[i] = aresta[num_arestas-1];
num_arestas--;
}
if((ys>=aresta[i].y_min)&&(ys<aresta[i].y_max)){ /* intersepta */
vxs[num_inters] = aresta[i].xs;
aresta[i].xs += aresta[i].delta; /* atualiza o xs */
num_inters++;
}
} /* for */
ordena(vxs,0,num_inters-1);
for(i=0;i<num_inters;i+=2)
if (vxs[i]+1 <= vxs[i+1])
}
} /* fill */
/* ordena as interseções */
hline(vxs[i],vxs[i+1],ys,0xff);
/* FIM */
Rasterização de Primitivas
11
Computação Gráfica Interativa - Gattass
2000.03.25
Ordenação no Algoritmo de Fill
static void ordena(int *vxs, int left, int right)
{
int i,j;
int a;
i = left;
j = right;
a = vxs[(left + right)/2];
do
{
while (vxs[i] < a && i < right) i++;
while (a < vxs[j] && j > left) j--;
if (i<=j)
{
int b = vxs[i];
vxs[i] = vxs[j];
vxs[j] = b;
i++;j--;
}
} while (i<=j);
if (left < j) ordena(vxs,left,j);
if (i < right) ordena(vxs,i,right);
}
Caso Particular:
Triângulo
y
A
c
b
B
a
C
x
Rasterização de Primitivas
12
Computação Gráfica Interativa - Gattass
2000.03.25
Stipples, patterns e
imagens
Stipple
void SetPixel(int x,int y)
{
int i=(x-x0)%w;
int j=(y-y0)%h;
h=5
if (stipple[i][j]) {
w=5
Pixel(x,y,foreground);
} else {
if (backopacity) Pixel(x,y,background);
}
}
Pattern
void SetPixel(int x,int y)
{
color = pattern[(x-x0)%w][(y-y0)%h]
Pixel(x,y,color);
}
Rasterização de Primitivas
13