ESTUDO DA APLICAÇÃO DOS CONDUTORES COMPACTOS EM

ESTUDO DA APLICAÇÃO DOS CONDUTORES
COMPACTOS EM LINHAS URBANAS DE 138 kV:
ASPECTOS ELÉTRICOS DE CORONA E RI
ALUNO: Edino Barbosa Giudice Filho
ORIENTADOR: Glássio Costa de Miranda
Belo Horizonte, Setembro de 2005
Edino Barbosa Giudice Filho
ESTUDO DA APLICAÇÃO DOS CONDUTORES
COMPACTOS EM LINHAS URBANAS DE 138 kV:
ASPECTOS ELÉTRICOS DE CORONA E RI
Dissertação de Mestrado submetida à banca examinadora designada
pelo Colegiado do Programa de Pós-Graduação em Engenharia
Elétrica da Universidade Federal de Minas Gerais, como parte dos
requisitos necessários à obtenção do grau de Mestre em Engenharia
Elétrica.
Área de Concentração: Sistema de Energia Elétrica
Orientador:
Professor Glássio Costa de Miranda
Universidade Federal de Minas Gerais
Belo Horizonte
Universidade Federal de Minas Gerais – UFMG
2005
iii
Dedico este trabalho ao meu Deus por suas bênçãos
Aos meus pais Edino e Léa, a minha esposa Eliane, pelo carinho e motivação
Aos meus queridos filhos Karolina, Wilson, Warlley, Laisson e Ana Paula
Aos meus netos Christofer e Kawã
In memorian Sebastiana F. Giudice e Sônia M.C.G.Giudice
iv
AGRADECIMENTOS
Agradeço a Deus, pois bem sei que todas as coisas só são possíveis através de sua vontade,
tendo colocado em meu caminho uma família abençoada e amigos que muito tem contribuído
para a realização dos meus sonhos.
Ao professor e amigo Glássio Costa de Miranda pelo incentivo, apoio e pelas suas palavras de
otimismo, além de sua dedicação e profissionalismo.
Ao professor José Osvaldo Saldanha Paulino pelo incentivo desde a origem e concepção dos
primeiros passos deste trabalho.
Aos meus amigos e colegas da CEMIG, cujo apoio e incentivo foram importantes, especialmente,
a ER/LT, e a todos que contribuíram de alguma forma para a realização deste trabalho..
v
RESUMO
Este trabalho apresenta um estudo comparativo do gradiente de potencial na superfície de
condutores LINNET tradicional e compacto, baseado em cálculo numérico utilizando o método de
elementos finitos e medições em laboratório da tensão de início de corona e da tensão de
rádiointerferência. A metodologia de cálculo é aplicada a um sistema de transmissão composto
por uma linha compacta, circuito duplo, sendo obtido o ruído de rádiointerferência usando-se os
condutores LINNET tradicional e compacto.
Os resultados mostram que as diferenças na geometria da superfície dos condutores LINNET
tradicional e compacto levam a gradientes de potencial 13% menores nos condutores compactos.
Este ganho representa uma diferença de 23% na tensão de início de corona, e 14% de redução
na faixa de passagem quando aplicados à linha compacta (138kV).
vi
ABSTRACT
This work presents the study for the development of the application of the national compact
conductor referring to the electric aspects of corona and radiointerference, where it is shown to the
performance of the conductor associated the urban and compact overhead transmission line of
138 kV with approach on the electric gradient on the surface of these conductors. A
predetermination of the security bands sizing of these overhead lines is carried out with detailed
study of the electric field behavior on the surface of these conductors. A comparison with other
types of conductors are carried out, where each model is represented in its actual form, showing
the different geometries of each wire that composes the most external layer of the conductor.
Special measurements of radio interference voltage and visual corona are carried out, comparing
the performance of the compact conductor with the conventional conductor and another compact
conductor model of high performance.
Based on the superficial electric potential simulations results of the conductors and
measurements, a surface factor is determined for the compact conductor. This study is used for
the adjustment of the existing predetermination calculation models for the radiointerference levels
on right of the way of overhead compact transmission lines of 138, showing the results gotten with
the application of this modeling.
vii
SIMBOLOGIA E ABREVIAÇÕES
A -
Ampères
b -
Pressão (Polegadas de Hg)
C -
Capacitância
[C] -
Matriz Capacitância
h
Altura do condutor ao solo
-
kV -
kiloVolt
m -
Fator de superfície
P -
Coeficiente de potencial de Maxwell
[P] -
Matriz dos coeficientes de potencial de Maxwell
q
Carga (C)
-
RA -
Ruído Audível
RI -
Rádiointerferência (dBµV/m)
t
- Temperatura (ºC)
T
- Temperatura (ºF)
TRI -
Tensão de radiointerferência (µV ou dBµV)
δ
- Densidade relativa do ar
ε0
-
µ0
- Permeabilidade do vácuo
φ
-
Potencial elétrico
ρ
-
Densidade de carga
Permissividade do vácuo
viii
SUMÁRIO
SIMBOLOGIA E ABREVIAÇÕES........................................................................................................................................VII
CAPÍTULO 1 - INTRODUÇÃO............................................................................................................................................... 9
1.1 - Condutores para Linhas Aéreas de Transmissão e Distribuição de Energia .....................................9
1.2 - Estrutura do Trabalho...........................................................................................................................11
CAPÍTULO 2 - O EFEITO CORONA EM LINHAS AÉREAS DE TRANSMISSÃO............................................................ 12
2.1- Corona em Corrente Alternada .............................................................................................................13
2.1.1- Corona Visual em Condutores de Linhas de Transmissão.................................................................14
2.1.2 - O Efeito Corona sob Chuva ..............................................................................................................15
2.2 - Rádiointerferência..................................................................................................................................15
2.2.1- Cálculo do Ruído de Rádiointerferência ............................................................................................18
CAPÍTULO 3 - ANÁLISE DO CAMPO ELÉTRICO NA SUPERFÍCIE DOS CONDUTORES............................................ 24
3.1 - Gradiente de Potencial Crítico..............................................................................................................24
3.2 - Gradiente de Potencial na Superfície do Condutor ............................................................................25
3.2.1 - Precisão dos Métodos de Cálculo......................................................................................................27
3.2.2 - Descrição dos Métodos de Cálculo ...................................................................................................27
3.3 - Método de Elementos Finitos ................................................................................................................28
3.3.1 - Análise dos Condutores acima do Plano de Terra.............................................................................31
CAPÍTULO 4 - RESULTADOS DAS MEDIÇÕES E SIMULAÇÕES .................................................................................. 34
4.1 - Medições..................................................................................................................................................34
4.2 - Cálculo do Gradiente de Potencial .......................................................................................................37
4.2.1 - Método Simplicado ...........................................................................................................................37
4.2.2 - Elementos Finitos..............................................................................................................................38
4.3 - Modelos Trifásicos Utilizando o Método de Elementos Finitos .........................................................38
4.3.1- Cálculo do Ruído de Rádiointerferência ............................................................................................43
CAPÍTULO 5 - CONCLUSÕES............................................................................................................................................ 45
REFERÊNCIAS BIBLIOGRÁFICAS.................................................................................................................................... 47
Capítulo 1 – Introdução
9
Capítulo 1 - Introdução
Economistas modernos, ao analisarem o grau de desenvolvimento de um país, baseiam-se
freqüentemente no consumo per capita de energia elétrica e no índice de crescimento desse
consumo, dada a sua ligação direta com a produção industrial e o poder aquisitivo da população.
Aumentar constantemente as potências disponíveis nos sistemas elétricos tornou-se, pois, uma
necessidade. Um regime de déficit energético representa poderoso freio ao desenvolvimento
sócio-econômico do país. As características peculiares de produção e distribuição de energia
elétrica, cujo fornecimento é considerado um serviço público, e, portanto, sujeito ao regime de
concessão por parte dos poderes públicos, pressupõem regimes de exclusividade em cada região,
estando, na maioria dos países, sob severa fiscalização, quando não parcial ou inteiramente nas
mãos dos próprios poderes públicos.
Na geração, transmissão e distribuição de energia elétrica, a seleção do tipo e dimensão do
condutor melhor adaptável para uma determinada Linha de Transmissão (LT), requer um
conhecimento detalhado das características dos tipos disponíveis de condutores. Tal seleção e
desenvolvimento de condutores para linhas aéreas de transmissão e distribuição tem se tornado
um desafio constante para os aspectos técnico e econômico [1, 2, 3]. O condutor usualmente
compromete em torno de 30 a 50% do total de investimentos (material e custos) da LT, podendo
ser considerado um dos mais importantes componentes da mesma. Além das características
mecânicas, os aspectos elétricos de corona e rádiointerferência (RI) do condutor a ser utilizado
em determinada linha de transmissão são fundamentais, mesmo em níveis de tensão mais baixos,
devido ao uso de estruturas compactas em regiões urbanas [4, 5].
1.1 - Condutores para Linhas Aéreas de Transmissão e Distribuição de Energia
O desenvolvimento técnico dos condutores para linhas aéreas [6, 7] mostra que os condutores de
cobre foram usados no período inicial de transmissão de energia por volta de 1880. Devido ao
peso elevado do cobre, os vãos das linhas de transmissão eram curtos, tornando-as mais caras,
tendo sido aos poucos substituído pelo alumínio no final do século XIX. As primeiras linhas aéreas
utilizando o alumínio para a transmissão de energia foram construídas na Califórnia em 1895. A
primeira linha aérea a utilizar um condutor com a formação de sete fios de alumínio foi implantada
em Connecticut em 1899 e permaneceu em operação por mais de 50 anos. Depois desta
instalação o uso dos condutores de alumínio cresceu continuamente, tornando-se praticamente o
único material utilizado nos dias de hoje.
Desde a introdução do alumínio em 1895, ter uma maior razão entre tensão mecânica e peso para
os condutores tem sido considerado uma vantagem comparando-se com o alumínio puro. Desta
forma um condutor composto feito de alumínio e aço foi introduzido em 1907. Esse condutor
combinava o baixo peso e elevada capacidade de condução de corrente do alumínio com a maior
força mecânica do núcleo de aço coberto de zinco. Esses condutores foram chamados de
Aluminium Conductor Steel Reinforced (ACSR), sendo utilizados na Alemanha desde 1920,
Capítulo 1 – Introdução
10
espalhando pelo mercado mundial por volta de 1930. A boa condutividade desses condutores
associada à razão tensão mecânica e peso e sua facilidade no manuseio foram as razões que os
mantiveram quase que exclusivamente em plena aplicação nos projetos das linhas aéreas durante
a primeira metade do século XX.
Depois de alguns experimentos realizados em 1921, uma nova liga de alumínio com magnésio foi
introduzida durante a década de 1930. Condutores com apenas um tipo de metal foram
desenvolvidos, o qual associava as mesmas características mecânicas e elétricas dos condutores
ACSR, reduzindo o peso e também melhorando a performance para corrosão. Esses condutores,
todo de alumínio liga, foram chamados All Aluminium Alloy Conductor (AAAC) e os condutores
compostos, Aluminium Alloy Conductor Steel Reinforced (AACSR), combinando esse material
com núcleos de aço, representavam alternativas para os condutores ACSR. No entanto, a
aplicação deste tipo de condutor não teve a mesma aceitação em muitos países, restringindo-se a
algumas aplicações especiais devido a um não esperado comportamento quanto a vibração.
Com o passar dos anos, entretanto, tem havido uma larga tendência de utilização dos cabos
AAAC quando comparados aos ACSR e até mesmo sob os condutores compostos AACSR, sendo
determinante a aplicação de maior peso. Inovações no projeto dos condutores tem aparecido no
mercado que seguem a tendência das mudanças requeridas pela indústria de eletricidade [8, 9,
10]. Novas ligas tem sido desenvolvidas mostrando uma melhor característica sob o aspecto de
estabilidade térmica e condutividade elétrica. Projetos inovadores têm melhorado o aspecto
quanto a vibração além de outras características especiais.
As primeiras publicações de condutores com as características geométricas dos condutores
compactos são datadas de 1930, com os condutores denominados Alumininum Condutor Steel
Reinforced - Self-Damping (ACSR/SD). São condutores com auto-amortecimento onde os fios de
alumínio redondos, com pequenos espaços entre eles e o núcleo de aço, proporcionam um
aumento na energia mecânica dissipada [10]. Analisando a literatura técnica [9, 10, 11, 12, 13,
14], desde os anos 50, verifica-se o desenvolvimento de geometrias especiais aplicadas a
condutores AAAC e AACSR para linhas aéreas de transmissão de energia elétrica. Somente na
década de 1960 os condutores do tipo AAAC/TW (Trape Wire), desenvolvidos no Canadá [12, 13],
tinham o encordoamento dos fios em camadas concêntricas, contendo um mínimo de duas
camadas de alumínio auto-amortecidas em formato trapezoidal, diminuindo os espaços entre os
fios e entre o núcleo de aço central do condutor.
Durante a década de 70, Boletins informativos da ALCAN ALUMINIO [12] apresentaram um
sumário dos dados da instalação em campo de condutores AACSR/SD. Condutores em liga de
alumínio, em forma de “pedra angular”, onde a formação própria e diferente de cada fio,
distribuído nas diferentes camadas, têm freqüência natural de vibração diferentes e tendem a
cancelar um ao outro, anulando as fortes vibrações eólicas no condutor, eliminaram a utilização de
amortecedores. Trabalhos recentes [2, 15] mostram os ganhos das superfícies compactas em
relação ao comportamento do condutor com relação ao deslocamento de ventos.
Capítulo 1 – Introdução
(a) Tradicional
11
(b) Compacto TW
(c) Compacto Aero Z
Figura 1.1 - Diferenças básicas entre um condutor tradicional e um condutor compacto [2]
Alguns outros artigos foram publicados com relação aos condutores compactos, mas a grande
contribuição nesta área veio com o projeto conjunto HIDRO QUÉBEC e ELECTRICITÉ DE
FRANCE, em 1996 [2, 8]. Em conjunto com grandes fabricantes foram desenvolvidos os
condutores de maior eficiência. O propósito desse programa foi estudar o comportamento desses
condutores e ter acesso às suas propriedades para uma eventual utilização nas redes e linhas de
transmissão, resultando em uma família de condutores especiais, dentre eles o condutor
compacto.
As características geométricas dos condutores compactos, além do uso de ligas especiais, levam
a ganhos de desempenho em relação aos condutores tradicionais. Nos condutores tradicionais, de
formação geométrica com fios redondos (Figura 2.1 (a)), os espaços vazios no interior do condutor
representam cerca de 25% do total da sua sessão reta. Nos condutores compactos TW (Trape
Wire), com a geometria dos fios em formato trapezoidal e nos condutores compactos Aero Z, com
geometria dos fios em forma de “Z”, preenchendo o mesmo como um quebra cabeças, Figura 2.1
(b) e (c), respectivamente, é possível reduzir este percentual de espaços vazios para quase 5%,
permitindo aumentar a potência de transmissão e/ou reduzir perdas térmicas [1, 2].
1.2 - Estrutura do Trabalho
Este trabalho está estruturado em 5 capítulos e referências bibliográficas.
O capítulo 2 apresenta um estudo sobre o efeito corona em linhas aéreas de transmissão e
distribuição de energia elétrica.
No capítulo 3 é apresentado um estudo dos métodos de cálculo do campo elétrico na superfície
dos condutores, bem como a metodologia utilizada nesse trabalho.
O capítulo 4 apresenta os resultados das medições e simulações realizadas, avaliando o
desempenho do condutor LINNET compacto TW em relação aos condutores LINNET tradicional e
LINNET compacto Aero Z.
Finalmente, no capítulo 5, são apresentadas as principais conclusões do trabalho e as propostas
para desenvolvimentos futuros.
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
12
Capítulo 2 - O Efeito Corona em Linhas Aéreas de Transmissão
Descargas de corona são formadas ao redor da superfície do condutor, quando a intensidade do
campo elétrico na superfície do mesmo excede o valor de disrupção do ar, gerando luz, ruído
audível, ruído de rádio, vibração do condutor, ozonio e outros produtos, causando perda de
energia [16]. O processo de ionização é geralmente iniciado por um campo elétrico capaz de
acelar elétrons livres em um meio gasoso [17]. Quando estes elétrons adquirem energia
suficiente, eles podem produzir íons positivos e elétrons livres através da colisão com átomos ou
moléculas. Os elétrons se multiplicam, como mostra a Figura 2.1, até que processos secundários
a partir do catodo possam tornar a descarga auto-sustentada. Os elétrons que iniciam o processo
de ionização também podem ser produzidos por foto-ionização. Durante a aceleração no campo
elétrico, o elétron colide com moléculas de nitrogênio, oxigênio, entre outros. Ocasionalmente, um
elétron pode se chocar suficientemente forte com um átomo, acarretando a mudança do nível de
energia de um ou mais elétrons deste átomo. O elétron que se chocou com o átomo perde parte
da sua energia na criação deste estado. Mais tarde, o átomo excitado pode retornar ao seu estado
normal, resultando na irradiação do excesso de energia na forma de luz (corona visível) e ondas
eletromagnéticas de freqüência mais baixa (radiointerferência). O elétron pode também colidir com
um íon positivo, transformando o íon em um átomo neutro [18].
Figura 2.1- Processo de ionização [18]
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
13
Em um campo elétrico não-uniforme gerado por um eletrodo negativo, os elétrons, acelerados por
este campo, através de choques inelásticos, produzem íons positivos e elétrons livres [17]. Por
serem mais leves, os elétrons serão rapidamente acelerados na direção contrária a do campo,
sendo que os íons positivos, mais pesados devido à sua massa, vão lentamente em direção ao
eletrodo, formando uma nuvem eletrônica ao redor do catodo. Com isto, o campo elétrico é
reduzido, fazendo com que os elétrons livres se recombinem. Através dos processos secundários,
estes íons positivos são adquiridos pelo eletrodo negativo, fazendo com que o campo retorne a
seu valor inicial. A energia requerida pelo processo representa a perda causada pelo corona [16,
17, 20, 21].
O processo de corona negativo é normalmente caracterizado por pulsos (“Trichel pulses”),
crescentes e decrescentes, e por “streamers” negativos. As amplitudes variam de 10-8A em
eletrodos de ponta a 20x10-8A em eletrodos arrendodados. A descarga inicial propaga-se em
torno de 20ns e é minimizada pela nuvem espacial. As constantes de tempo são entre 25ns e
50ns. Aumentando a tensão, aumenta a freqüência de ocorrência e diminui a corrente de
deslocamento. A freqüência máxima destes pulsos é de 2kHz para uma esfera de 8mm de
diâmetro e de 3MHz para um eletrodo cônico de 30º. Nos pontos de formação do corona negativo,
a luminosidade será fixa, em forma de esferas com colunas cônicas estendendo-se a partir do
eletrodo [17].
As descargas de corona positivo têm algumas das características descritas no processo de corona
negativo. O corona positivo tem 3 formas distintas, pulsos, crescimento Hersmtein, e “streamers”
positivos. Como o campo está em direção oposta, em relação ao processo de corona negativo, os
elétrons serão acelerados em direção ao eletrodo, mais rápido do que o afastamento dos íons
positivos. Desta forma, o eletrodo captura os elétrons livres, não ocorrendo diminuição do campo.
Este processo, mais complexo e demorado do que o corona negativo, tem tempos de formação de
30ns e decaimento da ordem de 100ns, com correntes da ordem de 0.25A, para um eletrodo
esférico de 8mm de diâmetro, e 0.003A para um eletrodo cônico. A máxima taxa de repetição é da
ordem de 200Hz para eletrodos largos, e 2kHz para eletrodos em ponta. Os “streamers” são
normalmente acompanhados por pulsos ionizados crescentes (crescimento Hersmtein). Esta
transição é normalmente gradual, resultando em descargas com pequenos picos acima de 2MHz.
Os “streamers” positivos (“breakdown streamers”) são então eliminados no eixo axial pelas cargas
espaciais negativas, com tempos de variação da ordem de nanosegundos [17].
2.1- Corona em Corrente Alternada
Sob condições de tensão alternada, todos os modos descritos anteriormente estarão presentes.
Entretanto, as cargas espaciais produzidas durante um semiciclo podem modificar o tipo e a
intensidade dos modos de corona que irão ocorrer no semiciclo subseqüente. Devido à mobilidade
dos elétrons no ar, as descargas de corona no semiciclo positivo da tensão de 60Hz, denominado
corona positivo, têm maior intensidade, coloração mais intensa (mais esbranquiçado), e ruído
audível mais intenso. As descargas de corona no semiciclo negativo (corona negativo) são menos
intensas, coloração mais avermelhada, e ocorrem com valores de tensão menores que o corona
positivo [17].
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
14
Sob condições normais de gradiente de tensão [16, 22, 23, 24], os condutores de linhas de
transmissão aéreas não apresentam grandes alterações na formação de corona em sua superfície
quando da variação climática. Irregularidades na superfície do condutor, tais como ranhuras,
aberturas, gotas de água e/ou poluição, farão com que o gradiente de tensão nestes pontos
específicos excedam o gradiente de disrupção do ar, tormando a fonte dominante de corona que
se generaliza pelo condutor.
2.1.1- Corona Visual em Condutores de Linhas de Transmissão
Peek [16, 19], em 1915, verificou experimentalmente que o fenômeno das descargas de corona
somente se iniciam com valores de gradientes de potenciais acima de 15kV/cm na superfície dos
condutores, quando também se iniciam as manifestações luminosas. O fenômeno é conhecido
como corona visual, e é um indicativo da presença da descarga do tipo “streamer” ou corona
positivo.
A presença de partículas estranhas aderidas ao condutor ou qualquer anomalia local pode
diminuir o nível de tensão ou gradiente para o qual o “streamer” começa a se manifestar. Em
função das cargas espaciais que podem alterar o campo elétrico, o “streamer” pode aparecer e
desaparecer. Desta forma, o aparecimento local de corona visual, devido ao “streamer” positivo,
define a tensão e o gradiente de corona visual. Mantendo-se a elevação da tensão, atingiremos
uma condição tal que a um certo nível de tensão e gradiente, o corona visual se manifesta em
toda a extensão do condutor. Nestas condições têm-se a tensão e gradiente de Peek [19], nas
quais as perturbações e perdas tornam-se elevadas. Continuando a elevar a tensão, o corona se
propaga nos pontos que ainda não se manifestaram de forma visual. Nestas condições, todos os
fenômenos devido ao efeito corona como rádiointerferência, ruído audível, perdas, apresentam-se
com intensidade semelhante àquelas verificadas para condições de chuva forte.
O tipo de descarga depende da configuração do campo elétrico sendo que, para eletrodos curvos
de superfície irregular, como os condutores de uma linha de transmissão, em conseqüência das
não uniformidades do campo elétrico, surgem descargas parciais na vizinhança da superfície dos
condutores, nos pontos onde a intensidade do campo elétrico é maior (nas irregularidades ou nos
pontos onde houver maior curvatura). Tais descargas, na vizinhança da superfície dos condutores,
são genericamente incluídas sob denominação de descarga corona. Neste caso o aumento da
corrente pode ser pequeno, pois, o corona inicial, embora seja uma descarga auto-sustentada,
ocorre numa pequena vizinhança dos condutores e não representa o fenomeno generalizado [17].
A análise do desempenho de uma linha de transmissão quanto a corona visual é feita calculandose de um lado o valor do gradiente crítico visual para um determinado condutor, que depende da
geometria própria do condutor e das condições atmosféricas e de outro determinando-se o valor
do campo elétrico superficial dos condutores, que depende também da geometria das estruturas
da linha de transmissão. Quando o campo elétrico superficial é maior que o gradiente crítico
visual, ocorre a transição das descargas do tipo não auto-sustentada para um dos vários tipos de
descargas auto-sustentadas, usualmente acompanhada de um brusco aumento da corrente
elétrica [25].
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
15
2.1.2 - O Efeito Corona sob Chuva
Durante as chuvas forma-se no condutor uma trilha de água que fica presa ao condutor. Ao se
extinguir as chuvas essa trilha, que se formou com o acúmulo de água na superfície inferior do
condutor, começa a se romper em forma de gotas, ou fica presa ao condutor até evaporar.
Existem casos em que a água se prende com maior intensidade à superfície do condutor
(hidrofilia) formando uma camada mais homogênea, e em outros casos em que a água tem
dificuldades em se manter aderida ao condutor formando uma camada desigual e cheia de gotas
(hidrofobia). A hidrofobia aumenta a tensão interfacial entre a água e o condutor, enquanto a
hidrofilia diminui a intensidade dessa tensão [17].
Tanto as perdas com tempo bom como aquelas sob chuva dependem dos gradientes de potencial
na superfície dos condutores. As perdas sob chuva dependem não só do índice de precipitações,
como também do número de gotículas d’água que conseguem aderir à superfície dos condutores.
Esse número é maior nos condutores novos do que nos usados, nos quais as gotas d’água
aderem mais facilmente à geratriz inferior dos condutores [26, 27, 28, 29, 30].
2.2 - Rádiointerferência
O rádio-ruído ou rádiointerferência devido às LT pode ser divido em duas categorias gerais:
interferências causadas por disrupção em pequenos gap’s (centelhamentos) ou descargas
parciais (corona). As fontes de interferência relacionadas às descargas em gap’s podem ocorrer
em isoladores, em condutores de amarração, entre partes metálicas das estruturas e em
equipamentos com defeitos, projetados ou instalados incorretamente. As descargas parciais,
devido ao efeito corona, são aquelas causadas pela disrupção do ar na superfície dos condutores
da LT.
O termo rádio-ruído é bem geral referindo-se a sinais na faixa de frequência de 3kHz a 30GHz.
Para se referir às interferências na faixa de freqüência abaixo de 30 MHz o termo
radiointerferência é utilizado. Esse termo foi primeiro empregado para descrever interferências
eletromagnéticas na faixa de rádio-difusão em AM (535-1605 kHz), estendida para cobrir uma
faixa de freqüência para a qual as interferências eletromagnéticas são similares àquelas
encontradas na faixa de rádio-difusão em AM.
O processo de descarga de corona ocorre em pulsos de tensão e corrente na linha de
transmissão, caracterizados por constantes de tempo de subida e decaimento da ordem de
microsegundos, e de forma repetitiva caracterizam um espectro de freqüência da ordem de alguns
megahertz. Os campos eletromagnéticos gerados por estes pulsos de corona tornam a linha de
transmissão uma fonte de distúrbio eletromagnético (ruído de rádio), em uma faixa da definição
genérica do termo [31, 32, 33].
Em teoria, o ruído de rádio gerado pelas linhas de transmissão pode interferir em qualquer
equipamento que opere à freqüência de rádio, dependendo de alguns fatores tais como distância
da linha ao equipamento de comunicação, a orientação da antena receptora, geometria da linha
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
16
de transmissão e das condições climáticas. A variação do ruído de rádio em função da tensão é
caracterizada por um aumento gradual do ruído com o aumento da tensão até o limite mínimo de
tensão no qual as perdas por corona são detectadas. Acima desta tensão, o aumento do ruído de
rádio é rápido, sendo que a taxa de crescimento é influenciada pelo diâmetro e superfície do
condutor. As linhas devem ser projetadas para que as tensões de operação nominais e
sobretensões temporárias não ultrapassem o valor de tensão onde o ruído de rádio cresce
rapidamente, comumente conhecido como joelho da TRI [34, 35, 36, 37, 38, 39].
As cargas produzidas pelo corona movendo-se no ar induzem cargas (isto é, corrente) no
condutor, dependente do modo de corona. Seja um condutor sob um plano de terra, como mostra
a Figura 2.2. O processo de descarga de corona é aproximado por um “streamer” plano, com uma
densidade linear de carga q0 por unidade de comprimento, movendo-se na direção radial ao
cilindro. Seja P0 o coeficiente de potencial de Maxwell entre esta linha de carga e o condutor. A
variação temporal da densidade de carga (q) induzida no condutor é a corrente gerada pelo
corona (corrente de ruído), dada pela expressão (2.1) [18],
i = − q0c
dP0 dρ
dρ dt ,
(2.1)
onde dρ dt é a velocidade da carga q0 e dP0 d ρ depende da posição relativa do condutor em
relação ao terra. Para este caso, pode-se mostrar que [18],
dP0
1
≈−
,
dρ
2πε 0 ρ
Figura 2.2- Geometria condutor plano [18]
(2.2)
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
17
ou seja,
i=
c
Γ,
(2.3)
q 0 dρ
,
ρ dt
(2.4)
2πε 0
Γ=
onde c é a capacitância por unidade de comprimento entre o condutor e o plano de terra e Γ é a
função de geração dependente somente das características do “streamer”, isto é, carga, posição e
velocidade [40, 41, 42, 43]. A relação entre a corrente de ruído e a tensão desenvolvida na linha
será dada pela impedância característica da mesma. Essa tensão é medida em laboratório e é
conhecida com Tensão de Radiointerferência (TRI),
TRI = Z 0 i .
(2.5)
Substituindo-se a expressão (2.3) na expressão (2.5) obtem-se a TRI em função da função de
geração ( Γ ),
TRI =
Z 0c
Γ.
4πε 0
(2.6)
O campo eletromagnético gerado por esta tensão de alta freqüência imposta ao condutor, a uma
distância x do mesmo, ao nível do solo, pode ser obtido através da expressão (2.7) [17],
E ( x) =
Z ar
2π
h
Γ,
 4h  2
2
ln  h + x
 d 
(
)
(2.7)
onde E(x) é o ruído de rádiointerferência, obtido em laboratório, em dBµV/m, Zar é a impedância
característica do ar, h é a altura do condutor e d o seu diâmetro. As medições da corrente de ruído
em laboratório [44], devem ser realizadas preferencialmente dentro de um recinto
eletrostaticamente blindado, o qual deve ser suficientemente grande para que as paredes, que
devem ser aterradas, não tenham efeito significativo sobre os campos na superfície do condutor.
Todos os circuitos de alimentação devem possuir filtros para evitar a introdução de perturbações
de origem externa. As medições devem, normalmente, ser realizadas com temperaturas entre
15oC e 35oC, pressão barométrica entre 870 e 1070 mbar e umidade relativa entre 45% e 75%. O
circuito de teste é composto por uma fonte de alta tensão conectada ao condutor através de um
filtro de rejeição, e um filtro passa-alta, com faixa de passagem nas freqüências de interesse (0,15
a 30MHz). As correntes de ruído geradas pelo condutor serão injetadas em uma resistência de
valor próximo à impedância característica da linha de transmissão, de tal forma que a queda de
tensão nesta resistência represente a tensão gerada pelo ruído de rádio advindo do efeito corona
(TRI).
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
18
Figura 2.3 - Característica do joelho da curva de radiointerferência verificado para cadeias duplas
de ancoragem em 500 kV para três condutores tipo RAIL
Os dados a serem analisados são as tensões pulsadas em µV (ou em dBµV), existente nos
terminais do resistor de acoplamento do filtro de alta freqüência, quando for aplicada tensão à
freqüência industrial no condutor. O valor padronizado para a resistência de acoplamento é de
300Ω. Como os valores de tensão aplicados ao condutor são elevados, o instrumento de medição
deve estar localizado a uma distância mínima de segurança. Para tanto, utiliza-se um cabo coaxial
para conectar a saída do resistor ao instrumento de medição. A impedância equivalente vista pelo
sistema deve ser de 300Ω.
A Figura 2.3 apresenta como exemplo uma medição da TRI para uma cadeia de ancoragem,
tensão nominal de 500 kV, com três condutores tipo RAIL por fase, onde observa-se o “joelho” da
TRI a partir de 350-370kV (47.6 dBµV), realizada pelo CEPEL (Centro de Pesquisas de Energia
Elétrica), para aplicação em linhas do Sistema CEMIG.
A função de geração pode ser obtida também a partir de dados experimentais, corrigidos para as
características particulares do sistema em estudo.
2.2.1- Cálculo do Ruído de Rádiointerferência
Estudos empreendidos em um grande número de instalações de pesquisas sobre transmissões
em extra e ultra-alta tensão conduziram ao estabelecimento de métodos de cálculo e fórmulas
para a predeterminação de níveis de RI, provocados por linhas de transmissão. Essas fórmulas
relacionam os níveis de RI com os parâmetros da linha, o gradiente de potencial na superfície dos
condutores, seus raios e o número de condutores por fase. Essas fórmulas, no entanto, não
explicam inteiramente as diferenças entre valores de ruído medidos em diferentes linhas, nem as
substanciais flutuações de níveis de ruído obtidas em uma linha ao longo do tempo.
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
19
Esses estudos verificaram, de fato, que os níveis de ruído de uma linha são basicamente instáveis
e extremamente sensíveis ao estado da superfície dos condutores. Mesmo com tempo bom,
foram observadas flutuações da ordem de 30% [16].
Um trabalho em parceria IEEE e CIGRÈ, de âmbito mundial, reconhecendo a ampla variação dos
níveis de RI e visando o estabelecimento de leis estatísticas válidas, reuniu dados de 75 linhas
das mais diversas configurações e com tensões acima de 230 kV, situadas em regiões de climas
diferentes. Esse trabalho foi iniciado em 1968 e suas conclusões foram publicadas em junho de
1972 [4], tendo sido os resultados das medições corrigidos e normalizados a fim de permitir sua
interpretação e análise estatística. Uma segunda etapa desse trabalho foi comparar esses
resultados com aqueles obtidos através dos vários processos de cálculo para a predeterminação
de RI [5], utilizando 10 metodologias diferentes desenvolvidas por grupos de pesquisa de diversos
países.
Esses métodos, de um modo geral, são empíricos ou semi-empíricos e permitem o cálculo do
desempenho das diversas linhas de transmissão em relação ao RI a partir de seus parâmetros de
projeto e das tensões de operação. Em todos esses métodos os níveis de ruído gerado pelas
linhas são determinados experimentalmente, havendo uma diferença básica no processo dos
métodos que o Comitê IEEE-CIGRÈ convencionou classificar como analíticos e comparativos.
Nos métodos analíticos, a grandeza característica da geração dos níveis de ruído, denominada
função de geração, é determinada em gaiolas de ensaios. Essa função é medida em instalações
monofásicas para diferentes arranjos de condutores, com condições de superfície conhecidas.
Empregando-se então os valores assim medidos pode-se calcular a totalidade das correntes de
ruído na LT e os campos resultantes em sua vizinhança. Os métodos comparativos empregam um
valor de referência bem definido do nível de ruído, medido em LT experimentais, utilizando-se de
fatores de correção para a geração do corona, freqüência de medição e distâncias laterais. A
equação característica básica para os métodos comparativos pode ser expressa pela equação
(2.8),
E = E 0 + E q + E d + E n + E D + E f + E fw ,
onde
E = em dBµV / m , é o nível de ruído de RI calculado (normas ANSI);
E 0 = valor de ruído de referência (característico das linhas sob estudo);
E q = fator de correção pela variação do gradiente;
E d = fator de correção pela variação do diâmetro do condutor;
E n = fator de correção pela variação do número de subcondutores;
E D = fator de correção pela variação da distância do condutor ao ponto de observação;
E f = fator de correção pela variação da freqüência de medição;
E fw = fator de correção para condições atmosféricas adversas.
(2.8)
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
20
Uma análise preliminar mostrou que, dentre as várias formulações encontradas na bibliografia
para a determinação do RI de linhas de transmissão [4, 5, 46, 47], algumas apresentam resultados
mais coerentes para linhas com tensão abaixo de 230 kV, apontados nas expressões (2.9) a
(2.12). O método FG (Alemanha), combina experiência prática com o conhecimento teórico dos
níveis de RI de linhas de alta tensão, apresentada na expressão (2.9),
 d 
 20 
 + En + 20 × K D × log  + E f + EFW ,
E = 53,7 ± 5 + K × (g m − 16,95) + 40 × log
D
 3,93 
onde
(2.9)
K = fator de correção do gradiente;
g m = gradiente máximo verificado na superfície do condutor (kV/cm RMS);
d = diâmetro do condutor (cm);
KD = fator de correção do diâmetro;
D = distância radial do condutor mais próximo à antena de medição (m).
O método Shiobara (Japão), expressão (2.10), representa o desenvolvimento de estudos de RI e
perdas por corona realizados em linhas de transmissão de 500 kV desde 1961,
 h 
 d 
 + 20 × K D × log 2  − 12(log f )2 − 17 log f , (2.10)
E = 30.0 + [(3.7 g m − 12,2 ± 3)] + 40 × log
D 
 2,53 


onde
f = freqüência do sistema de medição (Hz);
h = altura do condutor mais próximo ao solo (m).
O modelo comparativo da Westinghouse (USA), consiste em um relacionamento empírico
desenvolvido em vários anos de experiência nos testes de projetos de EHV, expressão (2.11),
 30.7h 
 d 
 + 20 log 2  − 10(1 − f ) .
E = 48.0 + 3.5[(g m − 17.5)] + 30 × log
 D 
 3,51 


(2.11)
O modelo comparativo da EGU (Czechoslovakia), expressão (2.12), foi obtido de estudos de RI
em laboratório e instituto de pesquisa, obtidos de linhas de 220, 400 e 500 kV entre 1962 e 1965,
E = 11 + 4.5gm − 34 log D − 22 log f − 15(log f )2 .
(2.12)
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
FG - Alemanha
Shiobara - Japão
21
Westinghouse - USA
Czechoslovakia - EGU
34
32
Nível de RI (dBuV)
30
28
26
24
22
20
2
4
6
8
10
12
Distância do eixo da LT (m)
Figura 2.4 – Comparação dos níveis de RI por uma linha de 138 kV
A Figura 2.4 mostra a comparação dos níveis de rádio interferência gerados por uma linha de
138kV, tipo L6 (padrão CEMIG), em função da distância lateral em relação ao centro da linha.
Neste caso, a distância D a ser utilizada nas equações (2.9) a (2.12) será,
D = h 2 + (11,5 − a) 2 ,
onde h é a altura do condutor mais próximo do solo e a é a distância deste condutor ao centro da
linha. Os valores de RI (em dBµV) foram calculados usando-se os métodos FG (Alemanha),
Shiobara (Japão), Westinghouse (USA) e EGU (Czechoslovakia). Como estes métodos são
desenvolvidos para linhas de transmissão de tensão nominal acima de 400kV, apresentam
diferenças de até 23% quando comparados para a LT de 138kV. Nota-se, pelo gráfico da Figura
2.4, que o método FG apresenta valores intermediários, quando aplicado a linhas com tensões
nominais mais baixas.
O método FG, usado neste trabalho para a predeterminação do níveis de RI em estruturas
compactas em 138 kV, representa um método monofásico [5], que calcula a intensidade de campo
de ruído devido à fase que maior contribuição fornece, obtido da configuração real da linha
trifásica. Esse modelo baseia-se no emprego de um valor de referência, com tempo bom, obtido
por meio de medições estatísticas bem definidas em linhas de ensaio e em linhas em operação
(valores 50% de probabilidade) com a aplicação de fatores de correção de acordo com a variação
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
22
de parâmetros e da tensão de operação. Para sistemas de 138kV, com um condutor por fase,
gradiente máximo entre 15 e 19kV/cm [16], as constantes
• K=3,5,
• En=-4dB,
• KD=1,6,
• Ef=0,
• EFW=0,
substituídas na expressão (2.9) resulta na expressão (2.13),
 d 
 20 
E = 49,7 + 3,5( g m − 16,95) + 40 log
 + 32 log  .
D
 3,93 
(2.13)
A Tabela 2.1 apresenta os valores de gradiente de potencial e RI, na superfície do condutor e no
limite da faixa de passagem padrão para LT de 138 kV, respectivamente, em função dos tipos de
condutores normalmente utilizados nestas linhas. A faixa de passagem é a distância em relação
ao centro da LT, de 11,5m para linhas de 138kV. Os valores de RI em função do diâmetro e do
gradiente de potencial na superfície dos condutores são apresentados nas Figuras 2.5 e 2.6,
respectivamente. A Figura 2.5 mostra que a variação dos níveis de RI, no limite da faixa padrão de
uma LT de 138 kV, são inversamente proporcionais ao diâmetro do condutor. A Figura 2.6 mostra
que a variação dos níveis de RI são diretamente proporcionais ao gradiente de potencial. Os
níveis de RI são significativamente afetados pelos valores do gradiente de potencial na superfície
do condutor (relacionados com os diâmetros dos condutores). Para valores de gradiente acima de
17kV/cm os valores de RI obtidos estão acima dos valores normais, como mostra a Figura 2.6.
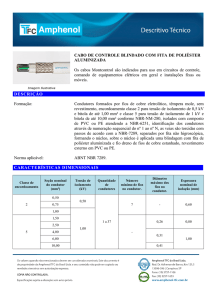
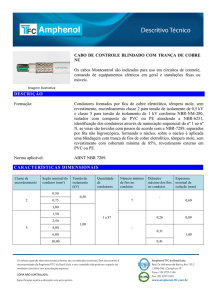
Condutor
Diâmetro do condutor
(cm)
Gradiente (kV/cm)
RI no limite da faixa
(dB)
RAIL
2,96
12,55
36,62
RUDDY
2,87
12,84
37,15
TERN
2,70
13,49
38,31
GROSBEAK
2,51
14,29
39,83
HAWK
2,18
16,01
43,4
LINNET
1,83
18,43
48,82
PENGUIN
1,43
22,48
58,75
Tabela 2.1 - Gradiente de potencial na superfície do condutor e níveis de RI gerados no limite da
faixa padrão de uma LT de 138 kV em função do diâmetro do condutor
Capítulo 2 – O Efeito Corona em Linhas Aéreas de Transmissão
23
65
60
55
RI (dBuV)
50
45
40
35
30
25
20
1
1,5
2
2,5
3
3,5
Diâmetro do Condutor (cm)
Figura 2.5 – Variação dos níveis de RI gerados no limite de uma faixa padrão de 138 kV
65
60
55
RI (dBuV)
50
45
40
35
30
25
20
10
12
14
16
18
20
22
24
Gradiente na Supefície do Condutor (kV/cm)
Figura 2.6 - Variação dos níveis de RI gerados no limite da faixa padrão LT de 138 kV em função
do gradiente de potencial na superfície condutor
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
24
Capítulo 3 - Análise do Campo Elétrico na Superfície dos Condutores
O gradiente crítico visual descreve o fenômeno das descargas de corona, verificadas
experimentalmente por Peek [19], quando também se iniciam as manifestações luminosas. Um
condutor atinge o gradiente crítico visual quando o gradiente crítico disruptivo é obtido a uma
determinada distância da superfície do condutor. O gradiente crítico visual depende apenas das
características geométricas do condutor e das condições do ambiente. O gradiente de potencial
na superfície do condutor é o campo elétrico superficial para uma determinada tensão aplicada ao
condutor, geralmente expresso em quilovolts por centímetro (kV/cm). O gradiente de potencial na
superfície do condutor depende da geometria da linha, associado à geometria do condutor e das
condições ambientais. Em um determinado sistema, se o gradiente de potencial na superfície do
condutor é maior ou igual ao gradiente crítico visual, os fenômenos decorrentes do efeito corona
estarão presentes, causando perdas, ruído de rádiointerferência, ruído audível, entre outros.
Desta forma, o conhecimento do gradiente de potencial na superfície do condutor é essencial no
projeto da linha de transmissão [48].
3.1 - Gradiente de Potencial Crítico
A determinação do campo elétrico crítico (Ec), é obtida através de uma fórmulação empírica
devida a Peek [19]. Assumindo um gradiente crítico disruptivo, sob um campo uniforme e nas
condições atmosféricas padrão (20ºC e 760mmHg), igual a 30 kV/cm, este será modificado devido
à superfície cilíndrica do condutor e as condições ambientais,
 0.301 
Ec = 30.m.δ .1 +
.
δ .r 

Na expressão (3.1), a parcela 0.301
(3.1)
δ .r corresponde a uma distância da superfície do condutor
denominada distância de energia, um valor do campo para o qual a energia armazenada pelo
campo elétrico é suficiente para desencadear o processo de disrupção. Nessa expressão, m
representa o fator de superfície do condutor, cujos valores, segundo Miller [19, 45], são
apresentados na Tabela 3.1. Pode-se observar que, em nenhum dos itens descritos nas
condições superficiais dos condutores, a geometria dos mesmos é considerada (fios redondos,
trapezoidais, etc). A partir do gradiente de potencial crítico, pode-se obter a tensão que, aplicada
ao condutor, inicia o processo de disrupção. Essa tensão é chamada de tensão de início de
corona e pode ser representada pela expressão (3.2),
Vc = rE c δ 2 / 3 ln(
2h
).
r
(3.2)
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
Tipo de
Condutor
1
2
3
4
5
6
25
Condições Superficiais dos Condutores
Fator de Superfície “m”
condutores cilíndricos, polidos e secos
cabos novos, secos, limpos e sem abrasão
cabos de cobre expostos ao tempo em atmosfera limpa
cabos de cobre expostos ao tempo em atmosfera agressiva
cabos de alumínio novos, limpos e secos, com condições de
superfícies decorrentes do grau de cuidado com que foram
estendidos nas linhas
cabos molhados, novos ou usados
1,00
0,92
0,82
0,72
0,53 a 0,73
0,16 a 0,25
Tabela 3.1 - Fatores de superfície [16, 45]
Nas expressões (3.1) e (3.2), δ = 0,386(760 − 0,086.h) (273 + t ) é a densidade relativa do ar,
sendo r o raio do condutor (cm), h a altura do condutor (cm), Ec o gradiente de potencial crítico
(kV/cm) e Vc, a tensão de início de corona (kV).
3.2 - Gradiente de Potencial na Superfície do Condutor
Fazendo uma breve análise dos métodos existentes para o cálculo do campo elétrico na superfície
dos condutores de LT’s [16, 48], verificamos que o solo é assumido ser uma superfície plana
condutora, horizontal e infinita, de potencial zero, e os condutores são assumidos serem cilindros
circulares infinitamente longos de superfícies lisas e equipotenciais, paralelos uns aos outros e ao
plano de terra, com conhecidos potenciais aplicados aos mesmos. A influência das estruturas
suportes dos condutores e outros quaisquer objetos não é considerada, o espaçamento horizontal
entre os condutores permanece constante em um valor especificado e a altura sobre o plano de
terra de cada condutor é um valor médio, considerando-se a flecha do condutor e a altura sobre o
plano de terra até o ponto suporte do condutor.
Desta forma, o problema de determinar o gradiente de potencial na superfície do condutor de uma
linha de transmissão é transformado na resolução do campo elétrico bi-dimensional de um
sistema de condutores cilíndricos paralelos sobre um plano de terra de potencial zero com
potenciais conhecidos aplicados aos cilindros. As cargas (Q) nos condutores são determinadas a
partir das tensões (V), através dos coeficientes de potencial de Maxwell,
[Q] = [P]−1 .[V ] ,
(3.3)
onde [Q] e [V] são vetores. Para uma linha de transmissão composta por n condutores, os
elementos da matriz [P] são dados pela expressão (3.4) e (3.5),
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
26
Pi i =
 2h
ln  i
2.π ε 0  ri



Pik =
D
ln  ik
2π ε 0  di k

,


1
1
,
(3.4)
(3.5)
onde hi é a altura do condutor i, ri é o raio do condutor i, d i k é a distância do condutor i ao
condutor k e Dik é a distância do condutor i à imagem do condutor k. A partir da carga em cada
condutor, o campo elétrico ( E ), na superfície dos condutores, é dado pelas expressões (3.6) ou
(3.7), onde ε 0 é a permissividade do vácuo,
[E ] =
[E ] =
1
1
[Q] ,
2 π r ε 0 ri
1
−1
  [P ] [V ] .
2 π ε 0 .  ri 
1
(3.6)
(3.7)
Para um condutor de raio r, a uma altura h do solo, o gradiente de potencial máximo na superfície
do mesmo ( E máx ), sob um potencial V, pode ser aproximado [44, 49] pela expressão (3.8),
1.1V
E máx =
onde o termo 1.1V
3
(
17.9
2h
b) r ln( )
459 + T
r
(
h
),
(h − r )
(3.8)
3 representa o valor da tensão fase-terra acrescido de 10%, o termo
(17.9 (459 + T )) b representa a correção devido às condições ambientais, temperatura (T oF) e
pressão (b inHg), e o termo (h (h − r )) representa a correção da altura do condutor.
Verificando as metodologias de cálculo existentes, observa-se que surgiram vários métodos para
o cálculo do gradiente de potencial em condutores aplicados a linhas aéreas de transmissão de
energia elétrica [16, 50]. Partindo da observação que por mais sofisticado possam ser os métodos,
com tempo computacional e complexidade considerados, caso não sejam contornados de modo
adequado os pontos de projeto de difícil ponderação, esses métodos podem se tornar pouco
eficazes [51].
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
27
3.2.1 - Precisão dos Métodos de Cálculo
De um modo geral, a precisão final do cálculo do valor do gradiente de potencial depende, não
somente do método de cálculo, mas também da precisão dos dados de entrada [16]. Desta forma,
alguns dos mais importantes dados que influenciam diretamente na precisão do valor final estão
relacionados aos parâmetros físicos da linha de transmissão, tais como o diâmetro do condutor, a
altura média dos condutores sobre o plano do solo, o espaçamento entre os condutores e a
tensão da linha.
Padrões existentes indicam que a tolerância no diâmetro do condutor é da ordem de 1% [48]. Uma
vez que o gradiente na superfície do condutor pode ser considerado quase que inversamente
proporcional ao diâmetro do condutor, isto pode resultar em valores de incerteza do gradiente da
ordem de 1%. A altura média dos condutores sobre o plano do solo é sujeita a variações devido a
flecha do condutor sofrer variações de acordo com a alteração da temperatura do condutor e
também devido ao efeito elétrico do plano de terra sob os condutores variar, uma vez que a
umidade do solo altera, conforme os níveis dos lençóis freáticos, perfis do terreno variáveis e
outros.
Da mesma forma o espaçamento entre os condutores deve variar segundo as condições do vento,
o que torna difícil uma simples correlação entre as variações nas alturas médias dos condutores e
os espaçamentos entre condutores com as correspondentes alterações nos valores do gradiente.
Uma vez que os condutores são considerados cilindros lisos, os gradientes calculados são valores
nominais e na realidade os condutores tradicionais ou os condutores de um modo geral são fios
encordoados e têm a superfície externa irregular contendo ranhuras, fendas, rugosidades,
materiais orgânicos e inorgânicos depositados em sua superfície.
Desta forma, seja qual for o método, como podemos verificar, uma série de fatores contribuem
inserindo um certo grau de incerteza nos valores calculados dos gradientes de potencial na
superfície dos condutores. Desde que nenhum controle pode ser exercido sobre alguns fatores já
mencionados, existe um mínimo de incerteza inerente ou própria nos valores de gradientes
calculados. Estudos mostram que se levados em consideração todos os fatores mencionados, um
valor otimizado, para um mínimo de incerteza seria em torno de 5% [48]. Com um erro admissível
de 1 a 2 % no método de cálculo, resulta em termo de um número que representa a incerteza
global entre 5.1 e 5.39%, mantendo o erro global dos valores de gradiente de potencial na
superfície dos condutores menor que 10% [48].
3.2.2 - Descrição dos Métodos de Cálculo
Analisando o Método dos Coeficientes de Potencial de Maxwell [17] e o Método de Markt e
Mengele [48], este último sendo o primeiro a sugerir um método de cálculo considerando o feixe
de condutores das linhas de transmissão, os efeitos do plano do solo e do feixe de condutores são
tratados independentemente. Na prática, entretanto, ambos os efeitos estão presentes
simultaneamente fazendo com que a carga total não seja igualmente dividida entre os
subcondutores do feixe de condutores.
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
28
O Método das Sucessivas Imagens [48], baseado no princípio de uma linha de carga imaginária
em um condutor cilíndrico paralelo de forma a manter a superfície do condutor como uma
equipotencial, é aplicado para representar a distribuição de carga nos condutores individuais do
sistema de multicondutores. Uma vez que cada processo de imagem sucessiva guarda a
equipotencial natural da superfície completa de um condutor no sistema, o processo converge no
limite para a solução exata de um sistema de multicondutores.
No Método dos Momentos [48], a distribuição de carga na superfície de cada condutor do sistema
de multicondutores é expandida em termos de uma série de harmônicos com desconhecidos
coeficientes (coeficientes de carga). Os coeficientes de carga desconhecidos para todos os
condutores são determinados para satisfazer as condições limites onde a superfície de cada
condutor é mantida em um dado potencial constante. Considerando um número suficientemente
grande de coeficientes de carga para cada condutor, o método dos momentos fornece a solução
exata para o campo de um sistema de multicondutores. Na prática, o número de coeficientes de
carga é escolhido, de forma a obter a desejada precisão.
O Método de Simulação de Cargas [48] deve ser considerado como uma versão simplificada do
método dos momentos para obter uma solução aproximada para o campo elétrico do sistema
multicondutor. A carga nos condutores é representada neste caso por um número de linhas de
carga localizadas uniformemente ao redor de um círculo dentro do condutor. A magnitude destas
linhas de carga é determinada para satisfazer as condições limites de potencial constante em um
número de pontos de teste igual ao número de desconhecidas linhas de carga na superfície do
condutor. A escolha do número, bem como a localização das linhas de carga, é bastante arbitrária
neste método, e a precisão é acertada através de experimentação numérica. O método tem o
inconveniente do condutor ser mantido como uma equipotencial somente nos pontos de teste e
desvia da equipotencial nos pontos intermediários. Técnicas numéricas [48] têm sido propostas
para melhorar a eficiência computacional do método para dadas precisões.
3.3 - Método de Elementos Finitos
Devido à necessidade de uma modelagem detalhada das formas das superfícies dos condutores,
comparando o modelo tradicional, com fios redondos, e o modelo compacto, com os fios em forma
de um trapézio, foi utilizado o programa QuickField [54]. Esse programa utiliza o Método de
Elementos Finitos (MEF), podendo-se observar o comportamento do campo elétrico em vários
pontos sobre as diferentes curvaturas e formas da camada mais externa do condutor, juntamente
com as geometrias compactas das estruturas de 138 kV sob estudo. O MEF tem sua origem no
campo da análise de estruturas [54,56], tendo sido aplicado a problemas de eletromagnetismo a
partir de 1968.
Considerando um campo eletrostático, em um meio homogêneo, não contendo cargas espaciais
presentes ou acumuladas, os potenciais poderão ser excitados de condições de contorno
(eletrodo metálico), entre os quais o material dielétrico é colocado [56]. Assumindo um sistema de
coordenadas cartesianas, para o campo Laplaciano, a energia elétrica (W) armazenada dentro de
uma área (A) da região sob estudo, em duas dimensões, pode ser descrita pela expressão (3.9),
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
2
 1   ∂φ  2
 ∂φ  
W = z ∫∫  ε x   + ε y   dxdy ,
2
∂x
 ∂y  
A 
   
29
(3.9)
onde εx e εy são os coeficientes anisotrópicos de permissividade. Para um material isotrópico
εx=εy=ε. A Figura 3.1 mostra esta situação, onde a área de interesse tem os potenciais Φa e Φb
como condições de contorno. O dielétrico pode ser dividido em duas partes (I e II), nas quais a
condição de contorno é conhecida. Neste caso W/z é a densidade de energia por elemento de
área dA.
A distribuição de potencial Φ(x,y) na região de interesse deve ser contínua e um número finito de
derivadas deve existir, sendo necessária uma discretização da região para o cálculo destes
potenciais. Utilizando-se de elementos triangulares distribuidos irregularmente e de tamanhos
arbitrários, como mostra a Figura 3.2, uma aproximação para o potencial no interior de um
elemento (e) pode ser expressa pelo polinômio,
φ e ( x, y ) = φ e = α 1 + α 2 x + α 3 y .
(3.10)
A expressão (3.10) mostra que o potencial dentro de cada elemento é linearmente distribuído.
Assim o campo elétrico é uniforme dentro de cada elemento,
Ee = −∇φe .
Figura 3.1 Problema de duas dimensões [56]
(3.11)
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
30
Figura 3.2 Elementos triangulares irregulares [56]
As constantes do polinômio da expressão (3.10) são obtidas utilizando-se os potenciais (Φi, Φj e
Φm) nos vértices do triângulo ((xi,yi), (xj,yj) e (xm,ym)) e aplicando-se o teorema de Cramer [56],
1
(aiφi + a jφ j + amφm ) ,
2∆ e
α1 =
α2 =
1
(biφi + b jφ j + bmφ m ),
2∆ e
α3 =
1
(ciφi + c jφ j + cmφm ) ,
2∆ e
(3.12)
onde
ai = x j ym − xm y j ,
bi = y j − ym ,
ci = xm − x j ,
a j = xm yi − xi ym ,
b j = y m − yi ,
c j = xi − xm ,
am = xi y j − x j yi ,
bm = yi − y j ,
cm = x j − xi ,
2∆ e = ai + a j + am = bi c j − b j ci ,
(3.13)
sendo ∆e a área do elemento triangular. A distribuição do potencial no elemento triangular pode
então ser obtida através dos nós adjacentes, equações (3.10), (3.12) e (3.13),
φ e ( x, y ) =
[
]
1
(ai + bi + ci )φi + (a j + b j + c j )φ j + (am + bm + cm )φm .
2∆ e
(3.14)
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
31
O método de elementos finitos é baseado na minimização da energia do sistema global, assim
somente as derivadas das energias que referem a distribuição espacial são de interesse. Da
equação (3.9), a densidade de energia para cada elemento é dada pela expressão (3.15),
2
2
 ∂φ  
W e 1   ∂φ 
= ∆ e ε x   + ε y    .
X =
z
2   ∂x 
 ∂y  e

e
(3.15)
Enquanto a função Χe só depende dos potenciais dos nós de cada elemento, uma função Χ para
todo o sistema irá existir. A formulação da energia total do domínio será mínima quando,
∂X
= 0,
∂{φ }
(3.16)
onde {Φ} é o vetor potencial para todos os nós dentro do sistema. Para um elemento específico, a
expressão (3.16) torna-se, na sua forma matricial,
∂X
e
∂{φ }
e
(
 bi 2 + c 2 i
ε 
= e 
4∆ e 
 sym
) (b b
(b
i
j
2
j
+ ci c j )
+ c2 j
(bi bm + ci cm )   φi 
) (b b
(b
j m
2
m
 
+ c j cm )  φ j  ,
+ c 2m  φ m 
)
(3.17)
e
∂X
e
e
= [h] {φ } .
e
∂{φ }
(3.18)
Com um sistema matricial que leva em conta a contribuição de todos os elementos triangulares da
região de interesse, como os potenciais no contorno são conhecidos, igualando-se a expressão
(3.18) a zero, e substituindo-se os potenciais conhecidos, obtem-se os potenciais nos nós de cada
elemento triangular, a partir dos quais obtem-se o potencial dentro de qualquer elemento da
região de interesse, e o campo elétrico (equação (3.11)) [56].
3.3.1 - Análise dos Condutores acima do Plano de Terra
A Figura 3.3, mostra uma configuração típica, para linhas de um condutor singelo, onde o plano de
terra é assumido ser um plano condutor perfeito com o potencial zero. O cabo encontra-se a uma
altura h do plano condutor e é modelado como uma superfície cilíndrica equipotencial, possuindo
simetria longitudinal. Na utilização do MEF, o domínio deve ser truncado através de uma condição
de contorno tal que possamos trabalhar com um número finito de incógnitas. A condição de
contorno deve modelar, pelo menos de forma aproximada, a distribuição de potencial longe da
fonte. Desta forma, deve-se considerar uma superfície de contorno, ao redor do condutor,
conectada ao plano de terra, como mostra a Figura 3.4, definindo a região de cálculo, de tal forma
que as linhas de campo no infinito sejam reproduzidas na região denominada domínio aberto.
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
32
Vo
h
V=0
Figura 3.3 - Condutor simples acima de um plano de terra
Vo
h
V=0
Figura 3.4 - Modelo truncado
Air
Figura 3.5 - Malha de elementos triangulares
Capítulo 3– Análise do Campo Elétrico na Superfície dos Condutores
33
A malha de elementos triangulares, gerada pelo programa, é mostrada na Figura 3.5. Nota-se
que, nas proximidades do condutor, existe um número muito maior de elementos triangulares do
que no contorno do domínio aberto.
Capítulo 4 – Resultados das Medições e Simulações
34
Capítulo 4 - Resultados das Medições e Simulações
4.1 - Medições
Utilizando-se amostras de condutores do tipo LINNET nas versões tradicional (fios redondos),
compacto TW (fios trapezoidais) e compacto Aero Z (fios em forma de “Z”), foram feitos vários
ensaios e medições. As medições de corona visual foram realizadas, inicialmente, para o condutor
tipo LINNET ACSR, diâmetro de 18,28mm, de 15m de comprimento, montado a 10m do plano de
terra, conforme mostra a Figura 4.1.
Esta figura apresenta os cuidados tomados durante a montagem do experimento, sendo
detalhado o uso de equalizadores de potencial nas extremidades do condutor. Estes
equalizadores eliminam interferências geradas pelas bordas do condutor. A medição de corona
visual [41, 49] foi obtida em total escuridão, sob condições de umidade entre 30 e 70%, com o
aumento gradual da tensão, atingindo o valor máximo de 110kV, sendo então diminuída
gradualmente até zero volts em três ciclos. O início de corona visual e a extinção são então
anotados como mostra a Tabela 4.1, e o valor médio dessas medições é então obtido.
Figura 4.1- Montagem do condutor LINNET para medição de corona visual
Tensão (kV- RMS)
CONDIÇÕES
Início
Extinção
1 Ciclo
84,0
83,0
2 Ciclo
83,0
82,0
3 Ciclo
84,0
83,0
Média
84
83
Tabela 4.1 – Resultados das medições em laboratório do corona visual
Capítulo 4 – Resultados das Medições e Simulações
35
A Figura 4.2 apresenta o circuito de teste utilizado na medição da tensão de rádio interferência.
Este circuito é composto por uma fonte de alta tensão (1), conectada ao corpo de prova (OE),
neste caso os condutores LINNET tradicional, compacto TW e compacto Z, através de um filtro de
rejeição (F). Em paralelo com o corpo de prova é conectado um filtro passa-alta (Ca). As correntes
de ruído geradas pelo condutor, ao aplicar-se tensão a frequência industrial, medida através de
um divisor de tensão (DT), são obtidas através da queda de tensão (Vm) em um resistor cujo valor
normalizado é de 300Ω [44, 49]. O instrumento de medição (2), localizado a 15m de distância do
sistema de alta tensão, está conectado ao resistor de medição através de um cabo coaxial cuja
impedância característica (Z) é de 50Ω . Para que a tensão medida (Vi) seja a tensão de rádio
interferência do sistema, a impedância equivalente vista pelos seus terminais (Zm) deve ser de
300Ω .
Os resultados obtidos com as medições de TRI são apresentados na Tabela 4.2, com valores em
microvolts e dBµV, média de três ciclos consecutivos. Os valores foram obtidos para degraus de
tensão de 10 kV (RMS). A Figura 4.3 apresenta o comportamento da curva de TRI, em µV, para
os condutores LINNET tradicional, compacto TW e compacto Z. A partir da tensão de início de
corona visual, obtida da Tabela 4.1 para o condutor LINNET tradicional (84 kV), inicia-se o joelho
da curva da TRI. Utilizando-se esta característica, foram obtidas as tensões de início de corona de
110 kV e 120 kV (RMS) para os condutores LINNET compacto TW e compacto Z,
respectivamente. Esses valores (tensões de início de corona) são estimados, representando o
primeiro salto da TRI em função da tensão aplicada aos condutores.
Ca = 1000 pF
F = 100 mH
Zi = 50Ω
(1) Cascata 0-1000 kV, 60Hz, Haefely
V Voltímetro RMS
(2) MicroVoltímetro Seletivo - B83600-C40
DT Divisor Capacitivo
Figura 4.2- Circuito de medição de TRI
Capítulo 4 – Resultados das Medições e Simulações
Tensão (kV)
0
20
30
40
50
60
70
80
90
100
110
120
130
140
150
LINNET
dB
15
15
15
15
16
16
28
61
62
63
66
69
74
77
80
uV
5,01
5,21
5,21
5,01
5,41
5,41
21,54
1000,00
1122,02
1211,53
1847,85
2511,89
4641,59
6556,42
9261,19
36
Compacto
dB
uV
15
5,01
15
5,21
15
5,21
15
5,01
16
5,41
16
5,41
17
6,07
17
6,56
17
6,56
29
25,12
62 1079,78
68 2238,72
73 4136,82
77 6556,42
80 9261,19
Compacto Z
dB
uV
15
4,82
15
5,21
15
5,21
15
5,01
16
5,41
16
5,41
17
6,07
17
6,56
17
6,56
18
7,08
28
23,26
64 1412,54
70 2928,64
73 4136,82
78 7356,42
Tabela 4.2 – Medições da TRI para os condutores LINNET
Figura 4.3 - Medição da TRI para os condutores LINNET e indicação do ínicio de corona visual
Capítulo 4 – Resultados das Medições e Simulações
CONDUTOR
Tensão Início de Corona
Valor Eficaz - medido
[kV]
TRADICIONAL
37
Gradiente Crítico Visual
[kV/cm]
(expressão 3.1)
Fator de Superfície
m
84
15.1
0,60
COMPACTO TW
110
19.9
0,79
COMPACTO “Z”
120
21.6
0,86
Tabela 4.3 – Determinação do fator de superfície para cada condutor
A partir dos valores obtidos da tensão de início de corona, utilizando-se as expressões (3.2) e
(3.1), para δ = 0.8873 (675 mmHg e 25 ºC), os valores do gradiente crítico e o fator de superfície
para cada um dos condutores foi obtido, como apresentado na Tabela 4.3. Observando-se os
resultados da Tabela 4.3, verifica-se que à medida que a forma da superfície externa do condutor
se aproxima do condutor ideal, o fator m se aproxima da unidade, como é o caso do condutor
LINNET compacto Z, e da mesma forma o gradiente crítico visual do condutor aumenta.
Os ganhos percentuais obtidos nas medições de tensão de início de corona, são de 23% para o
condutor LINNET compacto TW e 30% para o condutor LINNET compacto Z, em relação ao
condutor LINNET tradicional. Uma vez que tais ganhos foram verificados sob as mesmas
condições atmosféricas e os condutores têm o mesmo diâmetro, as características construtivas
dos condutores compactos, ou seja, a forma dos fios em sua superfície proporcionam diferenças
de até 10% no desempenho dos mesmos.
4.2 - Cálculo do Gradiente de Potencial
4.2.1 - Método Simplicado
O modelo simplificado, expressão (3.8), utilizado conforme recomendação da NEMA 107 [44], não
considera as diferenças na superfície dos condutores, utilizando apenas os fatores de geometria
do arranjo e condições atmosféricas.
Utilizando-se o mesmo valor de δ (0.8873), os valores calculados para o gradiente de potencial
máximo para os condutores ideal, LINNET tradicional e LINNET compacto (TW e Z), são
apresentados na Tabela 4.4, para tensão nominal de 138 kV. Nessa tabela, o condutor ideal é o
condutor cilíndrico perfeito. A tensão mínima necessária para que o gradiente na superfície
desses condutores atinja o gradiente crítico de início de corona é de 84.67 kVRMS.
Capítulo 4 – Resultados das Medições e Simulações
(a) Condutor Compacto
38
(b) Condutor Tradicional
(c) Condutor Ideal
Figura 4.4 - Modelo geométrico dos condutores utilizados nas simulações com o MEF
Tipo de
Condutor
Gradiente Crítico Visual
[kV/cm]
Expressão (3.1)
Ideal
Compacto “Z”
Compacto “TW”
Tradicional
25.0
21.6
19.9
15.1
Gradiente máximo superficial
Método Simplificado
[kV/cm]
Expressão (3.8)
14.5
14.5
14.5
14.5
Gradiente máximo superficial
MEF
[kV/cm]
12.0
12.3
12.3
14.7
Tabela 4.4 – Gradiente superficial e crítico visual dos condutores
4.2.2 - Elementos Finitos
O programa de cálculo utilizando o MEF (QuickField [54]), fornece o valor de gradiente na
superfície dos condutores com os fatores geométricos do condutor já levados em consideração.
Com base em três geometrias distintas, o condutor sólido ideal (cilindro perfeito), o condutor
LINNET tradicional (cabo com fios redondos) e o condutor LINNET compacto (cabo com fios
trapezoidais), foi feito um estudo detalhado do comportamento do gradiente de potencial na
superfície de cada condutor. A Figura 4.4 apresenta as três geometrias de condutores utilizadas,
analisadas a uma altura de 10m em relação ao solo. O condutor compacto representa as duas
variações analisadas nesse trabalho (compacto TW e Z). Na Tabela 4.4 são apresentados os
resultados dos cálculos utilizando o método de elementos finitos. Os resultados obtidos para os
condutores tradicionais, utilizando o MEF, é muito próximo daquele obtido utilizando-se o método
simplificado (1.5% de diferença). A diferença resultante da superfície do condutor é de 2.45 kV/cm
ou seja, um ganho de 17%, resultado este compatível com os ganhos obtidos experimentalmente.
4.3 - Modelos Trifásicos Utilizando o Método de Elementos Finitos
Uma análise trifásica da LT compacta de 138 kV se torna essencial devido à contribuição dos
campos elétricos produzidos por cada fase e os efeitos causados na superfície de cada condutor.
Nesse caso a disposição geométrica das fases definirá os níveis de campo na superfície de cada
condutor. A Figura 4.5 apresenta o estudo, contemplando no espaço, em relação a um plano de
Capítulo 4 – Resultados das Medições e Simulações
39
terra, do cálculo do gradiente na superfície dos condutores, considerando a forma geométrica de
cada condutor e a configuração da torre com as disposições reais das fases. A Figura 4.5 (a)
mostra a silhueta da estrutura compacta tipo CSLP, utilizada nesse trabalho, e as linhas de campo
elétrico em torno dos condutores, tradicional, compacto e ideal, Figuras 4.5 (b), 4.5(c) e 4.5(d),
respectivamente.
O estudo com cada tipo de condutor foi realizado com base nas disposições reais das fases na
estrutura, considerando uma altura de projeto de 7m e uma flecha de 3.45m a 75ºC, para um vão
médio de 100m e tensão de esticamento inicial de 302kgf, a 20ºC. A tensão na fase C foi
considerada máxima (1pu = 145kV), com as tensões nas fases a e b em -0,5pu. A disposição
geométrica dos condutores na estrutura, e os valores dos gradientes de potencial máximo na
superfície do condutor da fase C, é apresentada na Tabela 4.5. Pode-se observar que o gradiente
de potencial na superfície do condutor compacto é 13% menor em relação ao condutor tradicional.
(a)
Figura 4.5 - Torre compacta CSLP, padrão CEMIG e densidade de cores do campo elétrico na
superfície dos condutores, tradicional (b), compacto (c) e ideal (d)
Torre Compacta
CSLP
Condutor LINNET
GRADIENTE MÁXIMO SUPERFICIAL (kV/cm)
Fase C
Método Simplificado
Circuito duplo vertical (138 kV)
MEF
A
Tradicional
Compacto TW
Ideal
18.43
18.43
18.43
22.50
19.60
18.59
X
-1.6
1.6
Configuração das FASES (m)
B
C
Y
X
Y
X
Y
-1.6
-1.6
14
11.95
10
1.6
1.6
Tabela 4.5 - Gradiente de potencial na superfície do condutor
Capítulo 4 – Resultados das Medições e Simulações
40
Uma análise preliminar foi feita em relação à região de contorno e do número de nós utilizados no
cálculo do gradiente de potencial na superfície dos condutores. Uma regra básica [55] na definição
da região de contorno é a distância do centro do problema até o limite ser no mínimo cinco vezes
a distância do centro até os objetos de interesse. Para comparar e verificar a influência dessas
distâncias, na precisão dos resultados, colocamos o mesmo problema sob diferentes regiões de
contorno.
Como referência, temos o centro da estrutura compacta CSLP, tomando a fase C, mais próximo
do solo, como distância base. Para análise e ajuste das condições de contorno, uma comparação
com cinco valores diferentes para o semicírculo que limita essa região em torno dos condutores foi
realizada. Foram utilizados valores de 5, 6, 7, 10 e 15 vezes a distância base considerada. Para
cada distância um número de nós diferente é utilizado, já que a área do problema fica cada vez
maior. No primeiro caso, para uma distância de 50 metros (5 vezes a altura da fase C), temos um
total de 261757 nós. No último caso, com 150 metros (15 vezes), esse número passa para 337162
nós.
A Figura 4.6 apresenta o contorno da região sob estudo, onde um semicírculo em torno de todos
os condutores é estabelecido. A Figura 4.7 apresenta um detalhe de todos os condutores do
sistema sob estudo, mostrando a região de interesse com um número maior de nós.
A Figura 4.8 mostra como a densidade da malha de elementos finitos é maior nas proximidades
dos condutores. Na superfície do condutor o espaçamento dos nós é de 0,5 mm, chegando a um
espaçamento máximo de 1,3 mm entre os nós. Já na região de contorno, esse espaçamento
chega a 1 metro.
Figura 4.6 – Malha dos elementos finitos aplicados para estudo do gradiente na superfície dos
condutores para disposição vertical dos condutores – circuito duplo vertical em torres CSLP
compactas de LT de 138 kV
Capítulo 4 – Resultados das Medições e Simulações
41
Figura 4.7 – Análise da densidade de triângulos junto aos condutores e nas regiões da vizinhança
da estrutura compacta CSLP para 138 kV
Figura 4.8 – Dimensões dos triângulos junto às regiões nas proximidades do condutor, e em
pontos mais afastados
Capítulo 4 – Resultados das Medições e Simulações
42
A Figura 4.9 mostra a variação do campo elétrico máximo na superfície do condutor para as
condições de contorno de 5 (50m) a 15 vezes (150m) a distância base (10m), tendo-se um erro
percentual máximo de 0.67%. A Figura 4.10 mostra o comportamento do campo elétrico na
superfície dos condutores LINNET tradicional e compacto TW, ao longo do percurso e geometria
de cada fio que compõe a superfície externa do condutor. Observa-se uma melhor distribuição do
campo ao longo da geometria de fios compactos.
Figura 4.9 - Campo elétrico máximo na superfície do condutor ideal (cilindro perfeito)
E [V/m]
2500000
2000000
1500000
1000000
Compacto TW
Tradicional
500000
0
1,592
1,594
1,596
1,598
1,6
1,602 1,604
1,606
1,608
1,61
Distância ao longo da superfície do condutor [m]
Figura 4.10 - Campo elétrico na superfície dos condutores LINNET tradicional e compacto
Capítulo 4 – Resultados das Medições e Simulações
43
4.3.1- Cálculo do Ruído de Rádiointerferência
Como o gradiente na superfície dos condutores LINNET tradicional e compacto estão acima de
19kV/cm (22.5 e 19.6 kV/cm, respectivamente), as expressões (4.1) e (4.2) foram utilizadas para a
determinação do RI nos limites da faixa da LT de 138 kV com torres compactas, para os
condutores LINNET tradicional e compacto, respectivamente. Estas expressões representam a
expressão (2.16), aqui reproduzida pela expressão (4.3), modificada segundo a média dos limites
dos gradientes superfíciais verificados para os condutores LINNET tradicional e compacto,
 d 
 20 
ET = 49,7 + 3,5(g m − 21) + 40 log
 + 32 log  ,
D
 3,93 
(4.1)
 d 
 20 
E C = 49,7 + 3,5( g m − 19) + 40 log
 + 32 log  ,
D
 3,93 
(4.2)
 d 
 20 
E = 49,7 + 3,5( g m − 16,95) + 40 log
 + 32 log  .
D
 3,93 
(4.3)
A Tabela 4.6 apresenta os valores de RI obtidos a partir da aplicação das expressões (4.1), (4.2) e
(4.3) para a torre compacta CSLP, com tensão nominal de 138kV. São utilizados os condutores
LINNET tradicional e compacto TW, comparados com um condutor ideal. Estes valores são
apresentados em forma de gráfico na Figura 4.11.
Distância do eixo da LT (m)
20,5
19,5
18,5
17,5
16,5
15,5
14,5
13,5
12,5
11,5
10
9
8
7
6
5
4
3
VALORES DE RI - TORRE CSLP (dBµV/m)
Tradicional
Compacto TW
Ideal
41,42
42,11
42,83
43,57
44,35
45,16
46,00
46,89
47,79
48,72
50,18
51,17
52,16
53,12
54,03
54,84
55,50
55,97
38,27
38,96
39,68
40,42
41,2
42,01
42,85
43,74
44,64
45,57
47,03
48,02
49,00
49,97
50,88
51,69
52,35
52,83
36,17
36,86
37,58
38,32
39,1
39,91
40,75
41,64
42,54
43,47
44,93
45,92
46,91
47,87
48,78
49,59
50,25
50,73
Tabela 4.6 – Níveis de RI gerados pelas LT de 138 kV com torres compactas CSLP
Capítulo 4 – Resultados das Medições e Simulações
44
Considerando-se um valor de RI de 42 dB, máximo exigido para o limite da faixa de segurança de
LT (11,5m para linhas de 138kV), segundo a Agência Nacional de Energia Elétrica (ANEEL), para
o condutor tradicional teria-se que utilizar uma extensão maior para esta faixa, em torno de 18m.
Como pode ser observado, a utilização dos condutores compactos com esse tipo de torre permite
uma redução da faixa de passagem em relação aos condutores tradicionais (15,5m), com ganho
de 14%.
Tradicional
Compacto TW
Ideal
60
50
RI (dB)
40
30
20
10
0
0
5
10
15
20
25
Distância do eixo da LT (m)
Figura 4.11 - Níveis de RI gerados no ambiente pela LT compacta 138 kV, calculados para os
modelos de condutores estudados
Capítulo 5– Conclusões
45
Capítulo 5 - Conclusões
Os aspectos elétricos de corona e radiointerferência, abordados nesse trabalho, mostram a
evolução dos condutores compactos, representados pelo condutor LINNET compacto TW
(desenvolvido no Brasil) e LINNET compacto Aero Z. Nos estudos teóricos os condutores LINNET
compacto TW e Aero Z foram representados com características geométricas idênticas. Nos
ensaios em laboratório constatou-se que as formas em “Z” dos fios mais externos dos condutores
compactos Aero Z apresentam desempenho elétrico de corona 10% melhor que a forma
trapezoidal (condutor LINNET compacto TW).
As linhas de transmissão compactas, em virtude da presença de obstáculos e na maioria das
vezes em vias públicas, embora seja uma solução economicamente viável, apresentam níveis de
RI 40% maiores, quando comparados com os níveis de RI das linhas tradicionais para 138 kV e
que utilizam torres maiores.
A superfície mais externa do condutor com a geometria compacta dos fios permite reduzir a
tensão de início de corona em 23% para a geometria trapezoidal e 30% para a geometria Aero Z,
em comparação com os condutores tradicionais.
A geometria dos fios compactos permite uma melhor distribuição e comportamento do campo
elétrico na superfície do condutor, reduzindo o gradiente superficial em torno de 13% para a forma
trapezoidal de condutor compacto.
A redução do gradiente superficial dos condutores, quando utilizados com torres compactas
instaladas ao longo das vias públicas, permite a otimização da aplicação desse tipo de condutor e
estrutura, reduzindo as faixas dessas LT, quando comparados com os condutores tradicionais de
mesmo diâmetro, redução esta de até 14%.
A aplicação dos modelos comparativos, para a predeterminação dos níveis de RI, tem sido uma
prática empregada para todos os níveis de tensão, mesmo tendo sido desenvolvidos para tensões
acima de 400 kV. Apesar disso, notou-se que, para gradientes superficiais elevados, como
aqueles encontrados em linhas de transmissão compactas de 138kV, estas formulações ainda
necessitam de estudos mais aprofundados. Neste trabalho optou-se por corrigir os valores de
referência para os gradientes apresentados na formulação empírica, não tendo sido objetivo deste
trabalho a medição destes ruídos em linhas compactas.
A combinação de ambas as formas compactas, condutor e estrutura, abre uma ampla perspectiva
para auxiliar a otimização dos corredores das linhas de transmissão. Essas mesmas formas
compactas de estruturas aplicadas para a tensão de 138 kV necessitarão, a exemplo do estudo
apresentado em parceria IEEE e CIGRÈ [5], de uma ampla medição de RI ao longo de suas faixas
de passagem, o que poderá melhorar, certamente, o modelo de predeterminação de RI, utilizado
neste trabalho.
Capítulo 5– Conclusões
46
Contribuições do trabalho
Esse estudo contribui de uma forma geral para:
•
redução das perdas nas linhas aéreas de transmissão e distribuição de energia elétrica,
associado a um aumento do carregamento elétrico, aplicado a faixas de passagem cada
vez mais reduzidas, principalmente para as linhas urbanas que tem exigido distâncias de
segurança menores;
•
incentivar a continuidade do desenvolvimento e pesquisa do comportamento elétrico de
novas geometrias aplicadas a condutores com o desenvolvimento e parcerias nacionais;
•
ser mais uma alternativa como solução de projeto e construção ou mesmo de
recapacitação das linhas existentes, com a redução dos custos de um modo geral;
•
o setor elétrico nacional como mais uma opção eficiente para seleção e aplicação de
condutores nos projetos de linhas aéreas de transmissão e distribuição de energia elétrica.
Sugestões para Trabalhos Futuros
É importante a continuidade da investigação e avaliação sobre as adaptações aqui inseridas e
recomendadas nos modelos existentes para a predeterminação de RI no limite das faixas de
segurança das linhas de transmissão e distribuição de 138 kV, próximas aos centros urbanos, que
exigem faixas de passagem reduzidas. Tal procedimento deve contemplar também as LT de
230kV, utilizando condutores compactos de diâmetros maiores.
Esse trabalho direciona para a necessidade de se efetuar uma ampla medição dos níveis de RI,
nos limites das faixas de segurança, inicialmente para as LT urbanas de 138 kV, uma vez que os
métodos comparativos existentes foram baseados em linhas com tensões acima de 230-400 kV e
com características diferentes.
Após a instalação dos condutores compactos nacionais nas LT compactas, nas versões Liga
Termorresistente e Al 1350, o desempenho desses condutores devem ser monitorados sob
temperaturas mais elevadas, consolidando esse modelo de condutor e contribuindo para o
processo de utilização otimizada das faixas de LT.
Recomendamos que esse estudo se estenda para as configurações em feixe, utilizando não só os
condutores compactos desenvolvidos no Brasil, como também outros condutores especiais,
aplicados para tensões acima de 230 kV.
Referências Bibliográficas
47
Referências Bibliográficas
[1] GIUDICE, E. B. F.;
F.; MIRANDA, G.C.;
Compactos Aplicados
Seminário Nacional
Uberlândia, 2003.
NASCIMENTO, C..A M; GUIMARÃES, G. E.; BRAGA, G. E.; CAMPOS, O.
SALDANHA, J. O. P.; UEDA, S. M. Desenvolvimento de Condutores
a Linhas Aéreas de Transmissão e Distribuição de Energia Elétrica. In:
de Produção e Transmissão de Energia Elétrica - XVII SNPTEE.
[2] HYDRO QUÉBEC; ELECTRICITÉ DE FRANCE. Projet conjoint de recherche et d’essais sur
les conducteurs compacts, Août, 1996 and Joint research and testing project on compact
conductors, October, 1996.
[3] MARTIN, C.; SONCIN, A.; HENRIQUE, N. C.S. RI e TVI em decorrência de LT de 138 kV
Urbanas Compactas da COPEL. In: Seminário Nacional de Produção e Transmissão de
Energia Elétrica - VII SNPTEE. Brasília (DF), 1983.
[4] RADIO NOISE SUBCOMMITTEES. Survey on extra high voltage transmission line radio
noise. In: CIGRE Study Committee, n. 36, Working Group n. 1. In: IEEE Transaction on Power
Apparatus and Systems, v. PAS-92, n. 3, maio/junho, 1973.
[5] RADIO NOISE SUBCOMMITTEES REPORT. Comparison of radio noise prediction methods
with CIGRE/IEEE survey results”. IEEE Transaction on Power Apparatus and Systems, v. PAS92, n. 3, maio/junho, 1973.
[6] EN 50183
Conductors for overhead lines, aluminium, magnesium-silicon alloy wires. In:
Brussels, VDE Meeting, Verlag, 1985.
[7] THRASH, F. R. Transmission conductors, a review of the design and selection criteria. In:
Technical Support Resources. Carrolton, Southwire, 1999.
[8] GAUDRY, M. AT AL. Increasing the ampacity of overhead lines using homogeneous compact
conductors. In: Cigré Report 22-201, 1998.
[9] CIGRÉ SC22 WG12 TF1. Conductors for the optimal and design and uprating of lines, v. 1
and Conductors for increased capacity of overhead transmission lines, v.2 and Calculation of
conductor characteristics for use in their application. CIGRÉ Brochure, December, 2000 and
February, 2001
[10] CIGRÉ SC22 WG12 TF1. Conductors for the Uprating of Overhead Lines, v. 1 and Calculation
of conductor performance at elevated temperatures, v.2 and Conductor for increased current
capacity of overhead transmission lines. CIGRÉ Brochure, 29 January, 2002.
Referências Bibliográficas
48
[11] CIGRÉ SC22 – 12. Determintion probabiliste de la capacité thermique des conducteurs. In:
Electra, n. 164 p. 102-119, 1979
[12] ALCAN ALUMINIO. Summary field installation data on sdc and self-damping conductor. In:
Bulletin, fevereiro/1971
[13] CIGRE SC22-WORKING GROUP ON MECHANICAL OSCILLATIONS. Guide on conductor
self-damping measurements. In: Electra, n. 62, p. 79-90, January 1979.
[14] HOULE, S.; HARDY, C.; IAPOINT, A.; LOUIS, S.T. M., Experimental Assessment of SpacerDamper System Performance on Wind-Induced Vibrations of High Voltage Transmission Lines. In:
IEEE/CSEE Joint Conference on High Voltage Transmission Systems, Nº 87JC-39, 1987.
[15] VAN DYKE P.; HARDY, C.; LOUIS S.T.M.; GARDES, J.L. Comparative Field Tests of Various
Practices for the Control of Wind-Induced Conductor Motion. In: IEEE Transactions on Power
Delivery, vol. 12, Nº 2, April 1997.
[16] FUCHS, R.D. Transmissão de Energia Elétrica. Linhas Aéreas. Vol. 2, Editora Livros
Técnicos e Científicos S.A., 1979.
[17] BPA. Transmission Line Reference Book, 345kV and Above. 2 ed.: Electric Power
Research Institute, 1982.
[18] MIRANDA, G. C de. Uma contribuição ao estado do efeito corona em linhas de
transmissão utilizando o método de elementos finitos. Tese (Doutorado) - Universidade
Estadual de Campinas, 1994.
[19] PEEK, F.W. Dielectric Phenomena in High Voltage Engineering. Editora McGraw Hill,
1915.
[20] MARUVADA, P.S.; NGUYEN, D.H.; HAMADANI-ZADEH, H. Studies on Modeling Corona
Attenuation of Dynamic Overvoltages. In: IEEE Summer Meeting. Proc. of PES, 88~SM~538-7,
1988.
[21] CLADE, J.J.; GARY, C.H.; LEFEVRE, C.A. Calculation of Corona Losses Beyond the Critical
Gradient in Alternating Voltage. IEEE Transactions on Power Apparatus and Systems, v. 88,
pp 695-703, 1969
[22] MARUVADA, P.S.; MENEMENLIS; MALEWSKI, H. R. Corona Characteristics of Conductor
Bundles under Impulse Voltages. IEEE Transactions on Power Apparatus and Systems, v. 96,
pp 102-115, 1977.
[23] GARY, C.; TIMOTIN, A.; CRISTESCU, D. Prediction of Surge Propagation Influenced by
Corona and Skin Effect. IEE Proceedings, Pt. A, v. 130, pp 264-272, 1983.
Referências Bibliográficas
49
[24] CARNEIRO, S. JR. The Study of Corona and its Effects on Surge Propagation on
Transmission Lines, an Overview. In: Technical Meeting on Corona Models. Proc. of DCG/EPRI,
1987.
[25] NASSER, Fundamentos od gaseous ionization and plasma electrotronics. In: Wiley,
Interscience, 1971.
[26] CHANG, J.; LAWLESS, P.A.; YAMAMOTO, T. Corona Discharge Processes. IEEE 00933813/91, 1991.
[27] BELEVTSEV, A.A. Modern Theory of Corona Discharge. In: Proceedings of the 3rd
International Conference on Properties and Applications of Dielectric Materials, 1991.
[28] NGUYEN, T.T. Corona Discharge Streamer Model. IEE Proceedings-C, v. 139, pp 31-35,
1992.
[29] CARNEIRO, S. JR.; DOMMEL, H.W.; MARTI, J.R.; BARROS, H.M. An Efficient Procedure for
the Implementation of Corona Models in the Electromagnetic Transients Program. In: Proc. of
IEEE PES Summer Meeting, 93SM401-0 PWRD, 1993.
[30] SOWA, P. Transients on Transmission Lines Under Impulse Voltages with Corona Modelling.
In: Proc. of the 8th International Symposium on High Voltage Engineering, 1993.
[31] BUBE, L.; BONFANTI, I.; CORREIA, B.M.T.; VANDERSTOCKT, V. Using the simulation
language models with EMTP. In: Proc. of 11th Power Systems Computation Conference,
1993.
[32] ADAMIAK, K. Adaptive approach to finite element modelling of corona fields. IEEE
Transactions on Industry Applications, v. 30, p. 387-390, 1994.
[33] CHATIER, V.L.; BLAIR, D.E.; EASLEY, M.D.; RACZKOWSKI, R.T. Corona Performance of a
Compact 30kV Line. IEEE Transactions on Power Delivery, v. 10, p. 410-415, 1995.
[34] OLSEN, R.G.; SCHENNUM, S.S. A method for calculating wide band electromagnetic
iterference from power line corona. IEEE Transactions on Power Delivery, v. 10, p. 1535-1539,
1995.
[35] PHILIPS, A.J.; JANDRELL, I.R.; REYNDERS, J.P. Consideration of corona onset from a
water drop as a function of air pressure. IEE Proceedings-Sci. Meas. Technol., v. 143, p.125132, 1996.
[36] HALAHMI, E.; KRONIK, L. Color Corona Discharge Images. IEEE Transactions on Plasma
Sciense, v. 24, p. 87-90, 1996.
Referências Bibliográficas
50
[37] AL-HAMOUZ; AL-SHEHRI, Z.M. Inception voltage os corona in bipolar ionized fields and
efect on corona power loss. IEEE Transactions on Industry Applications, v. 34, p. 57-61,
1998.
[38] AL-HAMOUZ, Z.M.; ABDEL-SALAM, M. Finite element solution of monopolar corona on
bundle conductors. IEEE Transactions on Industry Applications, v. 35, p. 380-384, 1999.
[39] KIM, V.T.; WHANG, K.W. Two-dimensional numerical simulation of radial generation in the
positive corona discharge. IEEE Transactions on Plasma Science, v. 28, p. 261-265, 2000.
[40] YANG, J.; IZAWA, Y.; NISHIJIMA, K. Spectroscopic image processing and space charge
field for positive dc glow corona discharge in atmosphere. In: Proceedings of The 6th
International Conference on Properties and Applications of Dielectric Materials, 2000.
[41] YOUSSEF, M. The use of corona phenomena to measure the voltage of transmission lines.
In: IEEE Instrumentation and Measurement Technology Conference, 2001.
[42] KIRKICI, H. Electrical insulation in space environment. In: IEEE Annual Report Conference
on Electrical Insulation and Dielectrics Phenomena, 2001.
[43] MIN, W.; LEE, S.; KIM, H.; HAHN, S. Transient approach to steady state of discharge
phenomena in corona device. IEEE Transactions on Magnetics, v. 38, p. 485-489, 2002.
[44] NATIONAL ELECTRICAL MANUFACTURERS ASSOCIATION. NEMA–107: Methods of
measurement of radio influence voltage (RIV) of high-voltage apparatus. STANDARDS
PUBLICATION Nº 107, 1987.
[45] MILLER, C. J. Mathematical Prediction of Radio Interference and Corona Characteristics of
Smooth, Bundled Conductors. IEE, October, 1956.
[46] NILS, H.C.; KAZUMITU, Y.; CARLOS , E. O. C. Análise dos Métodos de Predeterminação de
Interferência em Rádio Baseada em Medições de Campo. In: Seminário Nacional de Produção
e Transmissão de Energia Elétrica – VII-SNPTEE, Brasília (DF), 1984.
[47] NILS, H.C.; KAZUMITU, Y.; CARLOS , E. O. C. Análise dos Métodos de Predeterminação de
Interferência em Rádio Baseada em Medições de Campo. In: Seminário Nacional de Produção
e Transmissão de Energia Elétrica – VII-SNPTEE, Brasília (DF), 1984.
[48] MARUVADA, P.S.; BACHA, R.J.; BACKER, A.C.; BLAIR, W.E.;BULAWKA, M.E.; CHARTIER,
V.I.; CORTINS, R.; CRAINE, L.S.; ELDER, G.R.; GARY, C.; HALL, J.F.; JANISCHEWSKYJ, W.;
KOLCIO, N.; MCDERMOT, T.J.; MORRIS, R.M.; NIGBOR, R.J.; ZAKALA, W.E.; PALDI, A.;
PERKINS, M.D.; REICHMAN, J.; REILLY, J.P.; RICHEDA, R.J.; SCHLINGER, W.R.; SEBO, S.A.;
TUTTLE, P.D.; WARBURRON, F.W.; WHITNEY, B.F.; WONG, P.S. A surfvey of methods for
calculating transmission line conductor surface voltage gradients.
IEEE Corona and Field
Referências Bibliográficas
51
Effects Subcommittee a Report Radio Noise Working Group on Power Apparatus and
Systems, v. PAS = 93 p 1660 – 1668, Sept./Oct. , 1974.
[49] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR-7876: linhas e equipamentos de
alta tensão, medição de radiointerferência na faixa de 0.15 a 30 MHz, método de ensaio, version
abril/1983.
[50] TIMASCHEFF. Fast calculation of gradients for the center phase of a three phase bundle
conductor line with any numer of subconductors. IEEE Transactions, Nova Iorque, v. PAS 90, n.
1, p. 157-164, 1971.
[51] TERMOSHOK, M. Relative surface gradients of grouped conductors. AIEE Transactions,
Nova Iorque,. v. 67. parte III. p. 1 583 -1 591, 1948.
[52] KALIFA, M.; ABDEL, M. S.; ALY, F.; ABOUSEADA, M. Electric fields around conductors
bundles of EHV transmission lines. IEEE Conference Papper, n. A 75 563 –7, 1975.
[53] SINGER, H.; STEINBIGLER, H; WEISS, P. A charge simulation method for the calculation of
high voltage fields. I EEE Transaction on PAS, v. 93. p. 1660-1668,1974.
[54] TERA ANALYSIS. Finite element analysis system. QuickField: Version 5.2, Janeiro 2005.
[55] CHEN Q.; KONRAD A. A review of finite element open boundary techniques for static and
quasistatic eletromagnetic field problems. IEEE Transactions on Magnetics, January, 1997.
[56] KUFFEL E. ; ZAENGL W. S. High Voltage Engineering Fundamentals. 2 ed. Pergamon
Press, 1984.