Lista - Arrays - UNIOESTE

EXERCÍCIOS DE COMPUTAÇÃO - ENGENHARIA
Prof. Jorge Habib Hanna El Khouri
1.
2.
UNIOESTE/PTI
16/05/2012
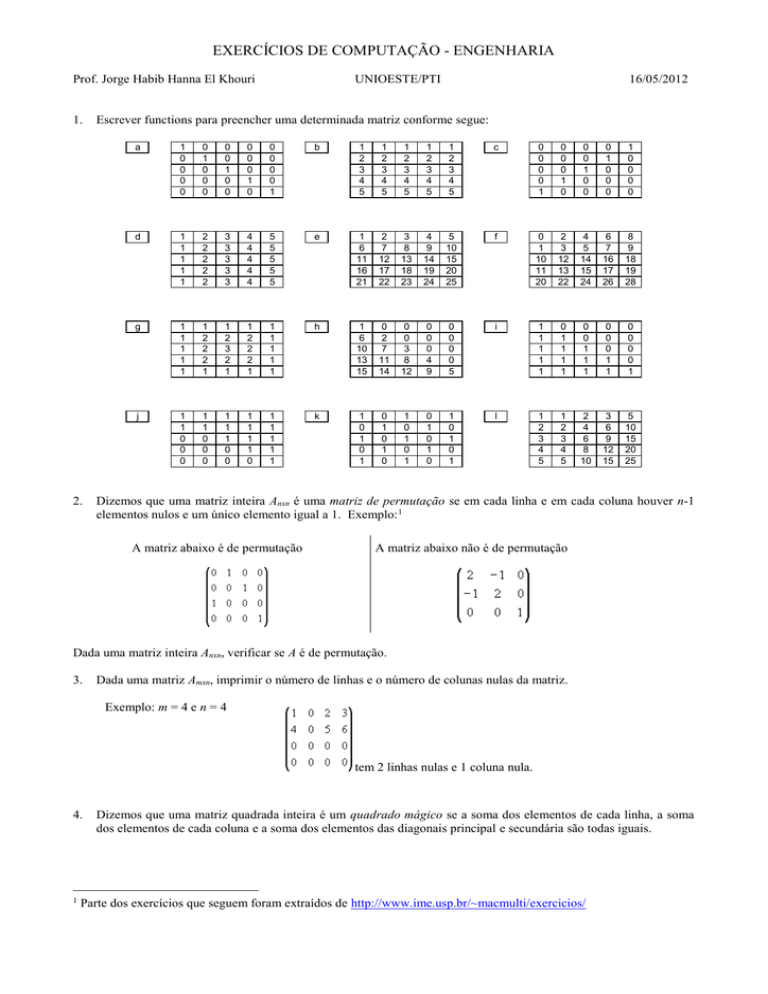
Escrever functions para preencher uma determinada matriz conforme segue:
a
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
b
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
c
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
d
1
1
1
1
1
2
2
2
2
2
3
3
3
3
3
4
4
4
4
4
5
5
5
5
5
e
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
f
0
1
10
11
20
2
3
12
13
22
4
5
14
15
24
6
7
16
17
26
8
9
18
19
28
g
1
1
1
1
1
1
2
2
2
1
1
2
3
2
1
1
2
2
2
1
1
1
1
1
1
h
1
6
10
13
15
0
2
7
11
14
0
0
3
8
12
0
0
0
4
9
0
0
0
0
5
i
1
1
1
1
1
0
1
1
1
1
0
0
1
1
1
0
0
0
1
1
0
0
0
0
1
j
1
1
0
0
0
1
1
0
0
0
1
1
1
0
0
1
1
1
1
0
1
1
1
1
1
k
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
l
1
2
3
4
5
1
2
3
4
5
2
4
6
8
10
3
6
9
12
15
5
10
15
20
25
Dizemos que uma matriz inteira Anxn é uma matriz de permutação se em cada linha e em cada coluna houver n-1
elementos nulos e um único elemento igual a 1. Exemplo: 1
A matriz abaixo é de permutação
A matriz abaixo não é de permutação
Dada uma matriz inteira Anxn, verificar se A é de permutação.
3.
Dada uma matriz Amxn, imprimir o número de linhas e o número de colunas nulas da matriz.
Exemplo: m = 4 e n = 4
tem 2 linhas nulas e 1 coluna nula.
4.
1
Dizemos que uma matriz quadrada inteira é um quadrado mágico se a soma dos elementos de cada linha, a soma
dos elementos de cada coluna e a soma dos elementos das diagonais principal e secundária são todas iguais.
Parte dos exercícios que seguem foram extraídos de http://www.ime.usp.br/~macmulti/exercicios/
EXERCÍCIOS DE COMPUTAÇÃO - ENGENHARIA
Prof. Jorge Habib Hanna El Khouri
UNIOESTE/PTI
Exemplo: A matriz
16/05/2012
é um quadrado mágico.
Dada uma matriz quadrada Anxn , verificar se A é um quadrado mágico.
5.
Um campeonato de futebol foi disputado por n times identificados pelos seus nomes. Para cada time são
considerados os seguintes dados:
PG - número de pontos ganhos (2 por vitória, 1 por empate, 0 por derrota)
GM - número de gols marcados
GS - número de gols sofridos (gols difíceis de marcar)
S - saldo de gols (GM - GS para os não atletas)
V - número de vitórias
GA - gol average (GM / GS, cuidado se GS = 0 )
(a) Dados os resultados de m jogos, imprima uma tabela com todos os dados (PG, GM, GS, S, V, GA, igual àquela que
sai no jornal) dos n times. Cada resultado é representado na forma (t1,t2,n1,n2) cuja interpretação é a seguinte: no
jogo t1 x t2 o resultado foi n1 x n2.
Exemplo: (São Paulo, Milan, 3, 2) que foi o placar da vitória que deu ao São Paulo o BICAMPEONATO
MUNDIAL.
(b) Com os mesmos dados do item (a), imprima a classificação dos times no campeonato (do primeiro para o último).
A classificação é pelo número de pontos ganhos (PG) e em segundo lugar pelo saldo de gols (S). Se houver empate
segundo os dois critérios, classifique os times envolvidos como.
(c) Um grupo de torcedores organizou um bolo sobre os resultados dos m jogos. Cada resultado certo vale 5 pontos
(inclusive o placar) ou 3 pontos (apenas o vencedor ou empate). Com os dados do item (a) e mais os palpites que
são compostos de m pares de números inteiros (p1, q1), (p2, q2), ... (pn, qn), onde o par representa o palpite do iésimo jogo, descubra o nome do ganhador do bolão.
6.
Faça uma função MAX que recebe como entrada um inteiro n, uma matriz inteira Anxn e devolve três inteiros: k, Lin
e
Col.
O
inteiro
k
é
um
maior
elemento
de
A
e
é
igual
a
A[Lin,Col].
Exemplo:
Obs.: Se o elemento máximo ocorrer mais de uma vez, indique em Lin e Col qualquer uma das possíveis posições.
7.
Faça um programa que, dado um inteiro n e uma matriz quadrada de ordem n, cujos elementos são todos inteiros
positivos, imprime uma tabela onde os elementos são listados em ordem decrescente, acompanhados da indicação
de linha e coluna a que pertencem. Havendo repetições de elementos na matriz, a ordem é irrelevante. Utilize
obrigatoriamente o procedimento da parte (a), mesmo que você não o tenha feito.
Ex.: No caso da matriz acima, a saída poderia ser:
Elem
8
7
5
4
3
3
Linha
1
0
2
2
0
2
Coluna
2
1
0
2
0
1
EXERCÍCIOS DE COMPUTAÇÃO - ENGENHARIA
Prof. Jorge Habib Hanna El Khouri
UNIOESTE/PTI
2
1
1
1
0
1
16/05/2012
1
2
0
ARRAY DE NÚMEROS
1)
Iniciar um vetor com um determinado valor;
2)
Iniciar um vetor com um valor randômico (estudar random e randomize);
3)
Obter o maior elemento;
4)
Obter o menor elemento;
5)
Obter a quantidade de elementos que se encontram em um intervalo dado (x1 e x2);
6)
Obter a soma dos elementos;
7)
Obter a média dos elementos;
8)
Obter o produto dos elementos;
9)
Obter a quantidade de vezes que um determinado elemento se repete;
10) Reverter (v1, v2, ...., vn)  (vn, ..., v2, v1);
11) Obter a soma de dois vetores; (elemento a elemento).
12) Obter a diferença de dois vetores;
13) Obter a produto de dois vetores;
14) Obter a divisão de dois vetores;
15) Somar um vetor com um valor escalar;
16) Subtrair um vetor de um valor escalar;
17) Multiplicar um vetor com um valor escalar;
18) Dividir um vetor por um valor escalar;
19) Fornecer a posição do maior valor;
20) Fornecer a posição do menor valor;
21) Dividir um vetor em dois outros ficando um destes vetores com p elementos;
22) Justapor dois vetores dando origem a um outro vetor;
23) Intercalar os elementos de dois vetores de tamanhos diferentes, dando origem a um outro vetor;
24) Obter o maior elemento entre as posições vi e vf.
25) Obter a posição do maior elemento
26) Trocar de posição o maior valor e o primeiro elemento.
27) Ordenar;
28) Dadas duas matrizes (A, la, ca) e (B, lb, cb) efetuar o produto matricial gerando resultado em (C, lc, cc).
29) Implemente um procedimento que recebe como parâmetros uma matriz, o número de linhas e colunas da matriz e
um determinado elemento X. O procedimento deverá efetuar a busca do elemento X na matriz, retornando suas
coordenadas e um código CODE=0 indicando sucesso. De forma similar deverá retornar CODE=1 (fracasso), para
o caso do elemento não estar na matriz.
30) Implemente um procedimento que recebe como parâmetros uma matriz, o número de linhas e colunas da matriz,
um determinado vetor e o número de elementos do vetor. O procedimento deverá efetuar a busca do vetor na
matriz, retornando suas coordenadas de início e um código CODE=0 indicando sucesso. De forma similar deverá
retornar CODE=1 (fracasso), para o caso do vetor não estar na matriz.
31) Implemente um procedimento que recebe como parâmetros uma matriz A, o número de linhas e colunas da matriz
A, uma matriz B com o número de linhas e colunas da matriz B. O procedimento deverá efetuar a busca da matriz
EXERCÍCIOS DE COMPUTAÇÃO - ENGENHARIA
Prof. Jorge Habib Hanna El Khouri
UNIOESTE/PTI
16/05/2012
B vetor na matriz A, retornando suas coordenadas de início e um código CODE=0 indicando sucesso. De forma
similar deverá retornar CODE=1 (fracasso), para o caso da matriz B não estiver inclusa em A.
32) Dados n e uma seqüência de n números inteiros, determinar quantos segmentos de números iguais consecutivos
compõem essa seqüência. Exemplo: A seguinte seqüência é formada por 5 segmentos de números iguais: 5, 2, 2, 3,
4, 4, 4, 4, 1, 1
33) Dados n e uma seqüência de n números inteiros, determinar o comprimento de um segmento crescente de
comprimento máximo. Exemplos: Na seqüência 5, 10, 3, 2, 4, 7, 9, 8, 5 o comprimento do segmento crescente
máximo é 4. Na seqüência 10, 8, 7, 5, 2 o comprimento de um segmento crescente máximo é 1.
34) Dizemos que um número natural n é palíndromo se

1º algarismo de n é igual ao seu último algarismo,

2º algarismo de n é igual ao penúltimo algarismo, e assim sucessivamente.
Exemplos:
 567765 e 32423 são palíndromos.
 567675 não é palíndromo.
Dado um número natural n > 10 , verificar se n é palíndromo.
35) Dizemos que uma seqüência de inteiros positivos é k-alternante se for composta alternadamente por segmentos de
números pares de tamanho k e segmentos de números ímpares de tamanho k.
Exemplos:
A seqüência 1 3 6 8 9 11 2 4 1 7 6 8 é 2-alternante.
A seqüência 2 1 4 7 8 9 12 é 1-alternante.
A seqüência 4 2 3 1 6 4 2 9 3 não é alternante.
A seqüência 1 3 5 é 3-alternante.
Dado n > 1 e uma seqüência com n inteiros, verificar se existe um inteiro k > 1 tal que a seqüência é kalternante. Dê como saída também o valor de k caso a seqüência seja alternante.
36) Dada uma seqüência de n números reais, determinar os números que compõem a seqüência e o número de vezes
que cada um deles ocorre na mesma. Exemplo: n = 8; Vetor: (-1.7, 3.0, 0.0, 1.5, 0.0, -1.7, 2.3, -1,7).
Saída:
-1.7 ocorre 3 vezes
3.0 ocorre 1 vez
0.0 ocorre 2 vezes
1.5 ocorre 1 vez
2.3 ocorre 1 vez
ARRAY DE STRINGS
37) Verificar a existência de um determinado string no vetor;
38) Retornar a posição de um string no vetor;
39) Contar as ocorrências de um string no vetor;
40) Ordenar alfabeticamente;
41) Ordenar de acordo com a quantidade de letras;
42) Ordenar de acordo com a quantidade de palavras;
43) Considerando como se fosse um vetor de nomes próprios, gerar um segundo vetor com os nomes intermediários
abreviados.