Linguagem Python e Séries de Fourier : Ferramentas - IFRS

Linguagem Python e Séries de Fourier : Ferramentas
para construção de material de apoio ao docente
Marcos Araquem Scopel [1] , Thayse Adineia Pacheco [1], Karina dos Santos Timboni [1]
Humberto Luz Oliveira[2]
[1]] Instituto
Federal de Santa Catarina (IF-SC), Campus Araranguá.
[2] Instituto Federal do Rio Grande do Sul (IFRS), Campus Osório
INTRODUÇÃO
O recém criado grupo de pesquisa foi idealizado para atender as demandas do também recente público formado de
acadêmicos do Curso de Licenciatura em Ciências Naturais com Habilitação em Física do IF-SC, Campus Araranguá. A idéia
desenvolvida em nossa linha de pesquisa é a de poder contribuir com o aprimoramento da formação desses acadêmicos, futuros
docentes e/ou pesquisadores, com subsídios diferenciadores que os potencialize para o sucesso em suas carreiras. Nesse sentido
propomos trabalhar com duas poderosas ferramentas, a linguagem de programação Pyhton e as Séries de Fourier.
O enfoque em nosso trabalho foi o de produzir material de apoio ao professor em sala de aula. Nessa fase, geramos scripts
em Python que reproduziram funções periódicas e suas respectivas expansões em Séries de Fourier, scripts de animações que
reproduziram a propagação de ondas, o fenômeno superposição, do batimento e da ressonância.
POR QUE USAR PYTHON ?
Como existem muitas linguagens de programação, essa normalmente é a primeira pergunta. Não há como respondê-la com
brevidade. Mas podemos enumerar alguns pontos fortes que tem influenciado centenas de milhares de novos programadores e
outros tantos experientes nessa área. As motivações mais comuns são [1]:
Qualidade do Software: Python dá enfoque a legibilidade, coerência e qualidade do software, sendo assim é mais fácil de
manter, muito mais que as linguagens de script tradicionais. Além disso, Python tem excelente suporte para mecanismos de
reutilização de código, como a programação orientada a objetos (POO).
Produtividade do desenvolvedor: O Python aumenta a produtividade do desenvolvedor muitas vezes além do que
conseguem as linguagens compiladas ou estaticamente tipadas como C, C++ e Java. O código em Python normalmente tem de
1/3 a 1/5 do tamanho do código equivalente em C++ ou Java. Isso significa uma economia nas etapas de digitação, depuração e
manutenção após o desenvolvimento. Os programas em Python são executados imediatamente, sem as cansativas etapas de
compilação e vinculação de algumas outras ferramentas.
Portabilidade do programa: Portar um código Python entre o unix, linux, windows e mac é apenas uma questão de copiar
o código entre os sistemas operacionais.
Bibliotecas de suporte: O Python vem com um grande conjunto de funcionalidades pré-compiladas e portáveis, conhecidas
como bibliotecas padrão. Essas bibliotecas suportam diversas tarefas de programação como aplicativos em ambientes gráficos
(GUI – Interface Gráfica com o Usuário) utilizando os módulos Tkinter (biblioteca nativo na instalação padrão Python),
programação numérica com uma vasta biblioteca com rotinas numéricas de fácil de utilização e construídas para obter
velocidade em “arrays”. Python pode ser utilizado para programação gráfica e de jogos através da biblioteca pygame.
Processamente de imagens com o pacote PIL, programação de IA com simuladores de redes neurais e muito mais.
Orientado a objetos: É uma linguagem completamente orientada a objetos, seu modelo de classes suporta noções
avançadas, como polimorfismo, sobrecarga de operadores e herança múltipla. Contudo, no contexto da sintaxe e tipagem
simples do Python, a POO é notadamente fácil de aplicar. Python pode ser utilizado como uma espécie de cola em outras
linguagens de programação (C, C++, Fortran, Java), pois há inúmeras implementações que possibilitam um desenvolvimento
de aplicações híbridas que unem o código python com essas linguagens. Um exemplo é a implementação Jython que gera o
bytecode de python em java.
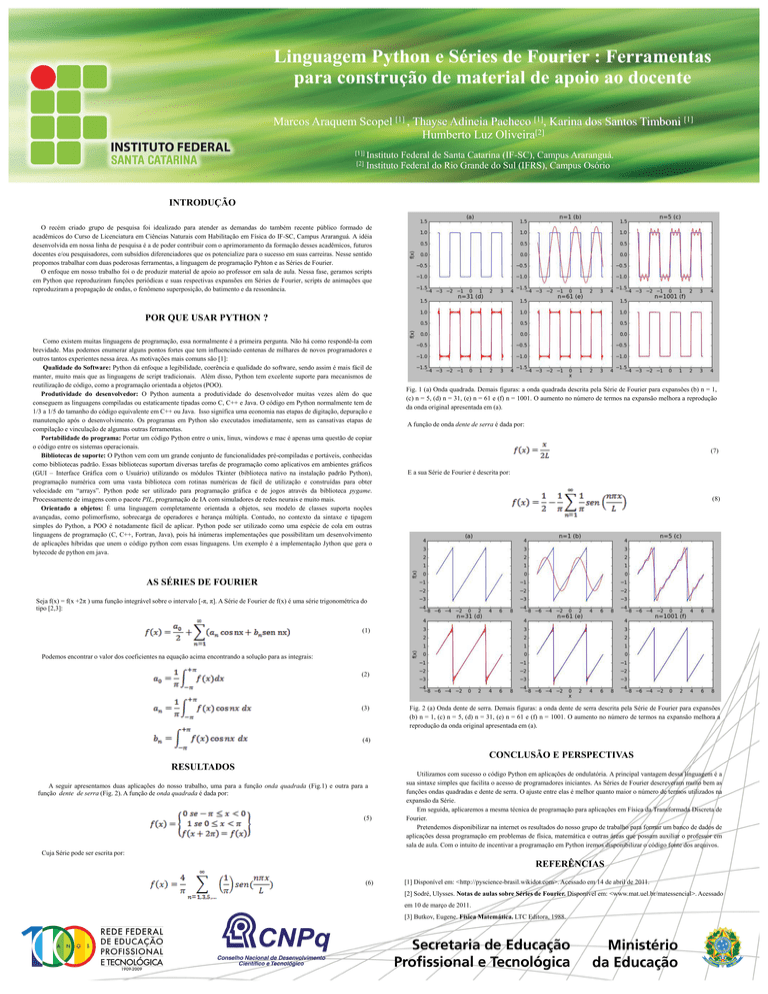
Fig. 1 (a) Onda quadrada. Demais figuras: a onda quadrada descrita pela Série de Fourier para expansões (b) n = 1,
(c) n = 5, (d) n = 31, (e) n = 61 e (f) n = 1001. O aumento no número de termos na expansão melhora a reprodução
da onda original apresentada em (a).
A função de onda dente de serra é dada por:
(7)
E a sua Série de Fourier é descrita por:
(8)
AS SÉRIES DE FOURIER
Seja f(x) = f(x +2π ) uma função integrável sobre o intervalo [-π, π]. A Série de Fourier de f(x) é uma série trigonométrica do
tipo [2,3]:
(1)
Podemos encontrar o valor dos coeficientes na equação acima encontrando a solução para as integrais:
(2)
(3)
Fig. 2 (a) Onda dente de serra. Demais figuras: a onda dente de serra descrita pela Série de Fourier para expansões
(b) n = 1, (c) n = 5, (d) n = 31, (e) n = 61 e (f) n = 1001. O aumento no número de termos na expansão melhora a
reprodução da onda original apresentada em (a).
(4)
CONCLUSÃO E PERSPECTIVAS
RESULTADOS
A seguir apresentamos duas aplicações do nosso trabalho, uma para a função onda quadrada (Fig.1) e outra para a
função dente de serra (Fig. 2). A função de onda quadrada é dada por:
(5)
Utilizamos com sucesso o código Python em aplicações de ondulatória. A principal vantagem dessa linguagem é a
sua sintaxe simples que facilita o acesso de programadores iniciantes. As Séries de Fourier descreveram muito bem as
funções ondas quadradas e dente de serra. O ajuste entre elas é melhor quanto maior o número de termos utilizados na
expansão da Série.
Em seguida, aplicaremos a mesma técnica de programação para aplicações em Física da Transformada Discreta de
Fourier.
Pretendemos disponibilizar na internet os resultados do nosso grupo de trabalho para formar um banco de dados de
aplicações dessa programação em problemas de física, matemática e outras áreas que possam auxiliar o professor em
sala de aula. Com o intuito de incentivar a programação em Python iremos disponibilizar o código fonte dos arquivos.
Cuja Série pode ser escrita por:
REFERÊNCIAS
(6)
[1] Disponível em: <http://pyscience-brasil.wikidot.com>. Acessado em 14 de abril de 2011.
[2] Sodré, Ulysses. Notas de aulas sobre Séries de Fourier. Disponível em: <www.mat.uel.br/matessencial>. Acessado
em 10 de março de 2011.
[3] Butkov, Eugene. Física Matemática. LTC Editora, 1988.