Lista nº 7

Aprimorando os Conhecimentos de Eletricidade
L ista 7
Associação de Resistores
Prof.: Célio Normando
1. (UNIFOR-97) O resistor R, que tem a curva característica representada no gráfico abaixo, é componente do
circuito representado no esquema.
Nesse circuito, os dados indicam que a diferença de potencial entre os pontos X e Y, em volts, é
a)
3,3
c) 10 e)
18
b)
6,0
d) 12
SOLUÇÃO: Do gráfico você calcula o valor da resistência R.
v
(volts)
60
N
tg = R  R =
60

3
R = 20

0
3
i (A)
No circuito os resistores estão em série.
R = 20 
x
i
z
i
10 
y
Vzy = 10 . i  6 = 10i
i = 0,6 A
i
Vxz = Ri  Vxz = 20 x 0,6
Vxz = 12V
x
y
A d.d.p. entre os pontos x e y será:
Vxy = Vxz + Vzy  Vxy = 12 + 6 
Vxy = 18V
RESPOSTA (E)
2. (UFRN-99) A figura abaixo representa um ramo de uma instalação elétrica residencial alimentada com uma
tensão de 220V. Compõe esse ramo um “relógio medidor de luz”, R, duas lâmpadas, L 1 e L2, um interruptor
ligado, S 1, e um interruptor desligado, S 2. Toda vez que Clara liga o interruptor S 2, observa que o “relógio” passa
a marcar mais rapidamente.
Isso acontece porque a corrente que circula no “relógio medidor de luz”, após o interruptor S 2 ser ligado, é:
a) igual à corrente que circulava antes e a tensão é maior que 220V.
b) maior que a corrente que circulava antes e a tensão permanece 220V.
c) menor que a corrente que circulava antes e a tensão permanece 220V.
d) maior que a corrente que circulava antes e a tensão é menor que 220V.
SOLUÇÃO: Verifique que com o interruptor S 2 desligado, somente a lâmpada L1, de resistência R, funciona sob
tensão V = 220V. A corrente no circuito é:
V
V = R . i 1  i1 =
R
 Com o interruptor S 2 ligado, as duas lâmpadas L1 e L2 funcionam em paralelo. Se as lâmpadas forem iguais as
correntes em cada uma, serão iguais.
V
R
 A corrente total no circuito i = i 1 + i2 aumenta, embora a tensão em cada lâmpada seja a mesma.
i1 = i 2 =
RESPOSTA (B)
3. (UFC-2000) No circuito mostrado abaixo, na figura (a), a corrente através da lâmpada L 1 é 1A e a diferença
de potencial através dela é 2V. Uma terceira lâmpada, L3, é inserida, em série, no circuito e a corrente através de
L1 cai para 0,5A [figura (b)]. As diferenças de potencial (V 1, V2 e V3), em volts, através das lâmpadas L1, L2 e L3,
são, respectivamente:
a) 2, 3 e 1
b) 2, 2, e 2
c) 1, 2 e 3
d) 2, 1 e 3
e) 3, 2 e 1
SOLUÇÃO: No circuito (a) as lâmpadas L1 e L2 estão em série.
L1
B
RESISTÊNCIAS DAS LÂMPADAS
VCB = R1 . i  2 = R1 x 1 
R1 = 2
i
VAC = R2 . i  4 = R2 . 1 
R2 = 4
L2
C
i
B
i
A
6V
No circuito (b) as lâmpadas L1, L2 e L3 estão em série.
VDB = V1 = R1 . i' = 2 x 0,5 
A
L1
B
i'
L2
D
C
i'
i'
V1 = 1V
B
A
6V
L3
A
i'
VCD = V2 = R2 . i' = 4 x 0,5 
V2 = 2 V
VAC + VCD + VDB = VAB  VAC = V3 
V3 + V2 + V1 = 6  V3 + 2 + 1 = 6  V3 = 3V
RESPOSTA (C)
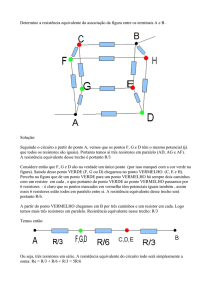
4. (UNIFOR-2001) Os circuitos 1, 2, 3 e 4 esquematizados a seguir contêm associações de resistores.
Dentre os circuitos, aqueles que contêm associação de resistores em paralelo são
a) 3 e 4
b) 2 e 4
c) 2 e 3
d) 1 e 3
e) 1 e 2
SOLUÇÃO:
Associações (1) e (4): Os resistores estão ligados entre pares de pontos diferentes, logo trata-se de uma
associação em SÉRIE.
Associações (2) e (3): os resistores estão ligados entre os mesmos pares de pontos, portanto os resistores
estão associados em PARALELO.
RESPOSTA (C)
5. (AFA-2003) Um fio condutor homogêneo de secção transversal constante de área A e comprimento , tem
resistência elétrica R. Esse fio é dividido em 10 pedaços iguais que são ligados em paralelo, formando um cabo,
cuja resistência vale R’. Assim sendo, pode-se afirmar que a relação entre R’ e R vale:
a) 1
b) 1/10
c) 10
d) 1/100
SOLUÇÃO: Quando o fio foi dividido em 10 pedaços iguais, cada pedaço passou a ter uma resistência R 1 dez
vezes menor que R.
R
R1 =
10
R
Quando ligados em paralelo a resistência equivalente R' = 1 .
10
R
R
Assim: R' = 10  R' =
100
10
R'
R
1

x

R 100 R
R'
1

R 100
RESPOSTA (D)
6. (UNIFOR-2002) Dois resistores, um de 50 ohms e outro de 100 ohms, estão associados em
paralelo. Se a intensidade de corrente no resistor de 50 ohms for igual a 2,0A, a intensidade de
corrente, em ampères, e a ddp nos terminais, em volts, referentes ao outro resistor são,
respectivamente,
a) 0,50 e 200
d) 4,0 e 25
b) 1,0 e 100
e) 4,0 e 100
c) 2,0 e 50
SOLUÇÃO: • Cálculo da d.d.p.
VAB  R1 . i1  VAB  50 x 2
VAB = 100 V
•
Cálculo da corrente (i2)
VAB = R2 . i2  100 = 100 . i2  i2 = 1A
RESPOSTA (B)
7. (UPE-2003) A figura apresenta a instalação do som de um automóvel. O som tem dois canais que serão
ligados, cada um, a dois alto-falantes. A impedância de saída de cada canal é de 8. A impedância é uma
espécie de resistência e segue as mesmas regras da associação de resistores em série e em paralelo. A
qualidade do som será melhor se a impedância de saída de cada canal for igual à impedância da associação
de alto-falantes ligada a ele. Considerando essas informações, escolha a alternativa correta.
a)
b)
c)
d)
A
A
A
A
ligação
ligação
ligação
ligação
(A)
(B)
(C)
(D)
está
está
está
está
correta
correta
correta
correta
se
se
se
se
os
os
os
os
quatro
quatro
quatro
quatro
alto-falantes
alto-falantes
alto-falantes
alto-falantes
forem de
forem de
forem de
forem de
8.
16.
8.
8.
e) A ligação (E) está correta se os quatro alto-falantes forem de 32.
SOLUÇÃO: Nas ligações A e E os alto-falantes ligados ao canal da direita estão associados em série, bem
como os que estão ligados ao canal da esquerda.
LIGAÇÃO (A) R = 8
Resistência equivalente em cada canal
RA = 8 + 8  RA = 16
LIGAÇÃO (E) R = 32
Resistência equivalente em cada canal
Re = R + R  Re = 64
Assim, nas ligações A e E a qualidade do som não é a melhor, pois a impedância em cada canal é MAIOR
que 8.
Nas ligações B e C os alto-falantes ligados aos canais da direita e da esquerda estão associados em
PARALELO.
LIGAÇÃO (B) R = 16
Resistência equivalente em cada canal
RB =
16
R
 RB =
 RB =8
2
2
LIGAÇÃO (C) R = 8
Resistência equivalente em cada canal
Rc =
R
8
 Rc =
 Rc = 4
2
2
Na ligação B a qualidade do som é a melhor, pois a impedância em cada canal é igual a 8.
RESPOSTA (B)
8. (MACK-2004) Um certo resistor de resistência elétrica R, ao ser submetido a uma d.d.p. de 6,00V, é
percorrido por uma corrente elétrica de intensidade 4,00mA. Se dispusermos de três resistores idênticos a
este, associados em paralelo entre si, teremos uma associação cuja resistência elétrica equivalente é:
a) 4,50
b) 3,0
c) 2,0
d) 1,5
e) 0,50
SOLUÇÃO:
 Para cada resistor:
R=
U
6

 R = 1,5 . 103 
3
i 4 . 10
 Para a associação de 3 resistores idênticos, cuja resistência é R, em paralelo:
R 1,5 . 10 3

Rp =
 Rp = 0,5 . 103  = 0,5k
3
3
R p = 0,5k
RESPOSTA (E)
9. (UECE-2004) Uma corrente elétrica de 10mA flui em um resistor de 100k  que está associado em paralelo
com outro resistor. Sendo de 30mA a corrente total neste trecho de circuito, o valor da resistência elétrica do
outro resistor, em k, é:
a) 10
b) 30
c) 50
d)100
SOLUÇÃO:
 Cálculo da ddp entre A e B.
VA B = 100 x 103 x 10 x 10– 3
VA B = 1000V
 Cálculo da corrente i2
iT = i1 + i2  30 = 10 + i2
i2 = 20mA.
 Cálculo da resistência R2
VA B = R2 . i2  1000 = R2 x 20 x 10– 3  R2 = 50.000
R 2 = 50k
RESPOSTA (C)
10. (UFPR-2005) Um técnico em eletrônica necessita de um resistor com resistência de valor não disponível no
seu laboratório. Então, utilizando alguns componentes existentes, ele monta uma associação de resistores
conforme mostra a figura abaixo.
Considerando que a diferença entre os pontos A e B seja igual a 9V, a corrente total i a ser fornecida é:
a) 1,8 A
b) 5,0 A
c) 0,60 A
d) 45 A
e) 0,16 A
SOLUÇÃO:
RESPOSTA (A)
GABARITO
01 E
02 B
03 C
04 C
05 D
06 B
07 B
08 E
09 C
10 A