Apostila

1
Moldando Pulso para reduzir a largura de banda
Pulsos quadrados não são práticos. São difíceis de serem gerados e requerem grande largura
de banda. Além disso, em razão da largura de banda limitada do canal, os pulsos transmitidos sucessivamente sofrem espalhamento no tempo, o que faz com que um pulso interfira
no outro. Esse efeito é denominado interferência intersimbólica (ISI). O espalhamento do
sinal não causará interferência se seguidas algumas condições, que combinam a resposta do
transmissor-canal-receptor, conhecidas como Nyquist Pulse shaping. Em outras palavras,
a resposta do sistema de comunicação (Tx, Rx e Canal) a cada instante de amostragem no
receptor é zero para todos os outros símbolos exceto o símbolo corrente.
(
k para n = 0
h(nTs ) =
(1)
0 para n 6= 0
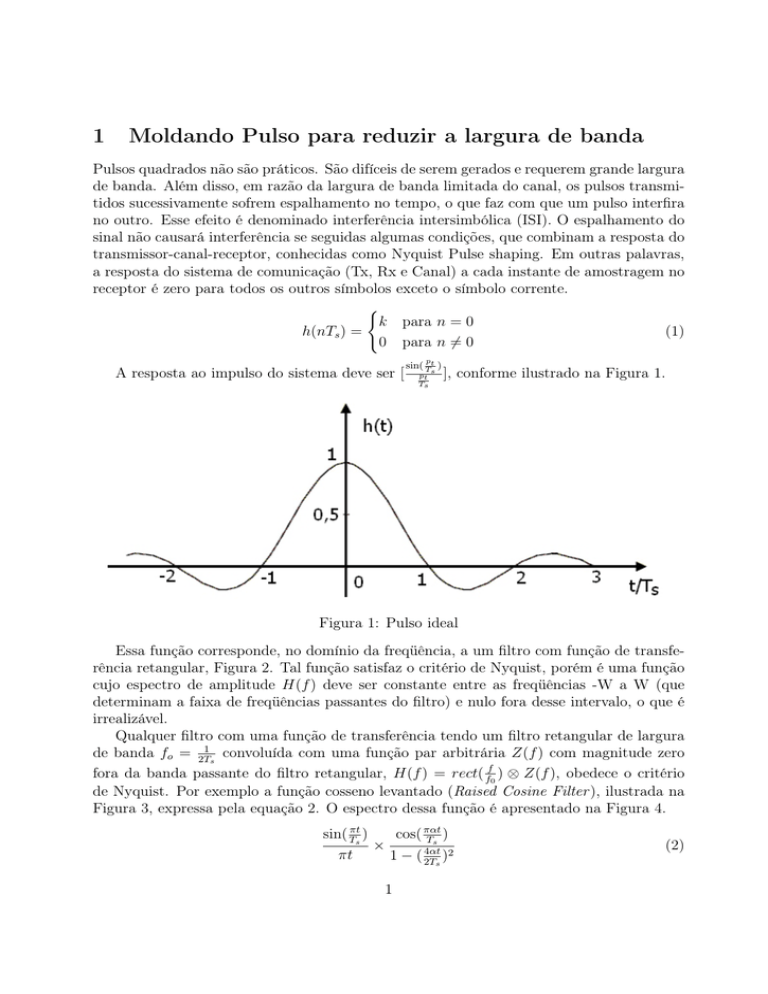
A resposta ao impulso do sistema deve ser [
p
s
sin( Tt )
pt
Ts
], conforme ilustrado na Figura 1.
Figura 1: Pulso ideal
Essa função corresponde, no domínio da freqüência, a um filtro com função de transferência retangular, Figura 2. Tal função satisfaz o critério de Nyquist, porém é uma função
cujo espectro de amplitude H(f ) deve ser constante entre as freqüências -W a W (que
determinam a faixa de freqüências passantes do filtro) e nulo fora desse intervalo, o que é
irrealizável.
Qualquer filtro com uma função de transferência tendo um filtro retangular de largura
de banda fo = 2T1 s convoluída com uma função par arbitrária Z(f ) com magnitude zero
fora da banda passante do filtro retangular, H(f ) = rect( ff0 ) ⊗ Z(f ), obedece o critério
de Nyquist. Por exemplo a função cosseno levantado (Raised Cosine Filter ), ilustrada na
Figura 3, expressa pela equação 2. O espectro dessa função é apresentado na Figura 4.
sin( Tπts )
πt
×
cos( παt
)
Ts
4αt 2
1 − ( 2T
)
s
1
(2)
Figura 2: Espectro do pulso ideal da Figura 1
Figura 3: Pulso cosseno levantado
2
Modulação de envelope constante
Não há mudanças descontínuas de fase, o sinal sofre menos distorções, o que é preferível
para as comunicações sem fio. A razão é porque os amplificadores trabalham aumentando
ou diminuindo a potência do sinal através de sua amplitude. Quanto mais a amplitude
variar, mais amplificações não lineares ocorrem. A modulação QPSK não é tecnicamente
uma modulação de envelope constante
2.1
Modulação offset QPSK – OQPSK
Consiste em uma variação da modulação QPSK Figura 5. O canal Q é deslocado por meio
tempo de símbolo, Figura 6, assim os canais I e Q não sofrem transições ao mesmo tempo.
As transições simultâneas podem causar mudanças descontínuas de fase. Por exemplo :
Símbolo 00 −→ Símbolo 11. No OQPSK esse tipo de transição não ocorre.
2
Figura 4: Espectro para pulso cosseno levantado
Figura 5: Constelação QPSK comparada a OQPSK
3
Modulação em amplitude e em fase – Quadrature
Amplitude Modulation – QAM
Neste tipo de modulação são alteradas as características de fase e amplitude do sinal. Por
exemplo, na modulação 16 QAM – Figura 7, se tem os sinais deslocados de 45o em fase
e em cada fase há uma variação de amplitude do sinal. Nesta modulação cada símbolo é
formado por 4 bits, portanto, se tem 16 símbolos para representar todas as combinações
possíveis de bits a serem enviados no canal de comunicação. A taxa de bits é então 4 vezes
a taxa de símbolos por segundo (bauds).
As constelações QAM podem ser classificadas em tipo I, II e III, como ilustra a Figura 8.
Em uma constelação do tipo I um número fixo de pontos de sinal (ou fasores) são espaçados
3
Figura 6: Exemplo de codificação OQPSK
igualmente em cada um dos N círculos, onde N é o número de níveis de amplitude. Na
constelação de tipo I, os pontos do anel interno estão mais próximos em distância e são mais
vulneráveis a erros. Para superar esse problema, a constelação do tipo II foi proposta, nesta
constelação, pontos de sinal ainda estão em círculos, mas o número de pontos no círculo
interno é menor que o número de pontos do círculo externo, fazendo a distância entre
dois pontos adjacentes no círculo interno aproximadamente igual a do círculo externo.
Na Constelação do tipo III é empregado o formato de um quadrado, sua análise mostrou
que tem uma pequena melhoria em desempenho sobre o tipo de constelação II, mas a
sua implementação seria mais simples que a do tipo I e II. Devido a isto, o tipo III é a
constelação mais utilizada1 .
Figura 7: Modulação 16–QAM
1
Digital Modulation Techniques – Fuqin Xiong, 2000
4
Figura 8: Tipos de modulação QAM1
4
Exercício
1. Para a seqüência de bits 11100100 realizar a modulação QPSK e OQPSK. Apresente
os diagramas para os canais I × t e Q × t para as referidas modulações.
5