Atividades em um laboratório virtual de eletricidade

Atividades em um
laboratório virtual
de eletricidade
Prof. Helder de Figueiredo e Paula
COLTEC
UFMG
PAULA, Helder de Figueiredo e
Atividades em um laboratório virtual de
eletricidade
[Recurso eletrônico] / Helder de Figueiredo e
Paula. - Belo Horizonte: COLTEC/UFMG, 2011.
56 p.
1. Eletricidade básica I. Título.
ISBN: 978-85-63515-03-2
CDD 620
CDU 62
Ficha catalográfica elaborada por: Reginaldo César
Vital dos Santos
(Bibliotecário CRB6/2165-COLTEC/UFMG)
Sumário
Apresentação..................................................................................
Informações iniciais sobre o simulador de circuitos ......................
Atividade 1 - Explorações iniciais ................................................
Exploração 1.1 - Ligando uma lâmpada a uma bateria .........
Exploração 1.2 - Inserindo um medidor de corrente elétrica
no circuito .....................................................................................
Exploração 1.3 - Ligando uma segunda lâmpada ao circuito
Atividade 2 - Simulando circuitos com ligações entre lâmpadas
idênticas .......................................................................................
Atividade 3 - Chaves interruptoras e curtos-circuitos ...................
Exploração 3.1 - Uso de chaves interruptoras ..........................
Exploração 3.2 - Curto-circuito em uma lâmpada ................
Exploração 3.3 - Curto-circuito total .....................................
Atividade 4 - Resistência de condutores metálicos e de associações de resistores ....................................................................
Exploração 4.1 - Resistência equivalente de uma associação
de resistores em série ...................................................................
Exploração 4.2 - Resistência equivalente de uma associação
de resistores em paralelo ..............................................................
Exploração 4.3 - Alterações nos filamentos e mudanças na
resistência das lâmpadas ..............................................................
Atividade 5 - Voltagem como medida da tensão e da diferença de
potencial elétrica ...........................................................................
5.1. Polaridade e tensão elétrica como recursos para a caracterização de fontes de energia ......................................................
5.2. Como se define a unidade de medida da tensão elétrica
5.3. Uma analogia entre pressão hidráulica e tensão elétrica
5.4. Diferença de potencial em circuitos série e paralelo ......
Atividade 6- Medidas de tensão em um circuito elétrico .....................
Exploração 6.1- Associação de baterias ................................
Exploração 6.2- Voltagem em trechos específicos do circuito
Atividade 7- Potência elétrica de um elemento de circuito ................
Atividade 8- Ligando duas lâmpadas diferentes em um mesmo
4
6
7
7
8
9
10
11
11
11
12
13
13
14
14
17
17
18
18
19
22
22
23
24
circuito ..........................................................................................
Atividade 9 - Sobrecarregando uma bateria ..................................
Atividade 10 - Previsões e desafios em circuitos mistos ....................
Exploração 10.1 - Lâmpada em série com associação de lâmpadas em paralelo ........................................................................
Exploração 10.2 - Lâmpada em paralelo com associação de
lâmpadas em série ........................................................................
Exploração 10.3 - Circuito em paralelo formado por dois conjuntos de lâmpadas em série .........................................................
26
27
29
29
30
31
Apresentação
Este livro foi concebido para ajudar estudantes da Educação Básica, ou
pessoas interessadas em compreender circuitos elétricos, a aprender
os principais conceitos, modelos e teorias que organizam essa área do
conhecimento científico e tecnológico. Mais especificamente, este Atividades em um Laboratório Virtual de Eletricidade propõe várias atividades
com o intuito de orientar a realização de experimentos simulados em um
computador. A realização das atividades aqui propostas não substitui ou
diminui a importância da interação do usuário deste livro com um professor. No caso de pessoas já desvinculadas do ambiente escolar, o uso
deste livro não substitui o estudo autodidata de bons livros didáticos ou
paradidáticos que tratam do mesmo assunto ou o contato com pessoas
mais experientes em termos de conhecimentos básicos em eletricidade.
4
Os experimentos aqui propostos são similares aos que podem ser desenvolvidos com o uso de baterias, lâmpadas, fios metálicos, interruptores e
medidores elétricos. Mas os comportamentos de objetos reais, tais como
os que acabamos de mencionar, diferem dos comportamentos exibidos
pelas simulações, em algumas situações específicas. Pilhas e baterias
reais, por exemplo, têm limitações no que diz respeito à quantidade de
energia que são capazes de fornecer a cada segundo. No computador,
todavia, esse tipo de limitação pode não aparecer. Lâmpadas reais, por
sua vez, apresentam um comportamento razoavelmente complicado, mas,
no computador, a maioria das simulações apresenta as lâmpadas como
objetos que se comportam de maneira simples e previsível.
Apesar dessas diferenças e do alerta que elas emitem em relação às
diferenças entre circuitos reais e circuitos simulados, nós acreditamos que
os experimentos simulados têm uma contribuição importante, no que diz
respeito à aprendizagem das ciências. Isso porque, ao representar um
fenômeno natural ou tecnológico no computador, nós podemos “misturar”
aquilo que observamos ao lidar com fenômenos reais com aquilo que
imaginamos a partir das ideias e teorias que as ciências criaram para
compreender esse fenômeno. Isso nos autoriza a dizer que o experimento
simulado promove uma fusão entre o mundo vivido (aquele que julgamos
vivenciar e observar) e o mundo concebido (as coisas que imaginamos
para compreender o que vivenciamos e observamos). Também nos autoriza a concluir que as simulações não substituem os experimentos realizados com materiais concretos, do mesmo modo que esses últimos não
substituem as simulações. Assim, em uma situação ideal, tanto simulações
quanto experimentos com materiais concretos deveriam ser realizados.
Uma vantagem dos experimentos simulados, dado o fato de que muitas
simulações são gratuitas e amplamente acessíveis, é que sua realização
não apresenta custo algum, além do gasto da energia elétrica necessária para manter o computador em funcionamento. Além disso, apesar da
complementaridade dos experimentos simulados aqui propostos e dos experimentos que podem ser realizados com materiais concretos, é possível
dar um passo inicial importante na aprendizagem de ideias e procedimentos básicos necessários à manipulação e à construção de circuitos lidando
apenas com o uso das simulações.
As atividades aqui reunidas utilizam duas simulações criadas pelo projeto
Physics Education Technology (ou projeto PHET), da Universidade do
Colorado. Muitas das simulações desenvolvidas por esse projeto, incluindo as que usaremos aqui, estão traduzidas para o português e podem
ser acessadas no endereço http://phet.colorado.edu/en/simulations/translated/pt, quer seja para serem executadas on line, quer seja para serem
“baixadas” para a memória do computador. Desse modo, podemos rodar
as simulações sem estarmos ligados à internet. Além desse endereço,
essas simulações também podem ser acessadas no site do Banco Internacional de Objetos Educacionais (BIOE) do Ministério da Educação do
Brasil (http://objetoseducacionais2.mec.gov.br/).
Para usar essas simulações em seu computador você deverá ter instalado, previamente, o aplicativo Java. Se você escolher a função Run Now
no primeiro endereço eletrônico apresentado acima e se o seu computador não tiver tal aplicativo instalado, basta seguir os links para realizar a
instalação. O software necessário para rodar arquivos criados em Java,
como as simulações que usaremos nas atividades a seguir, é totalmente
gratuito, seguro e pouco exigente em termos de memória e capacidade de
processamento do computador.
Faça as atividades aqui propostas e consulte um bom livro para ter acesso
a informações e explicações complementares. Além de livros de Física do
Ensino Médio, você poderá consultar o capítulo 10 (Eletricidade em nossas
casas) que compõe o livro de 9o ano da Coleção Construindo Consciências
(Apec, Editora Scipione, 2010). O autor deste e-book é também coautor
desta coleção. O estudo dos circuitos elétricos é fascinante: divirta-se!
5
Informações iniciais sobre o
simulador de circuitos
A maioria das atividades propostas a seguir está baseada no aplicativo
em Java Circuit Construction Kit DC [ou Circuitos de Corrente Contínua (DC)]. Esse aplicativo permite montar circuitos contendo lâmpadas,
baterias, fios condutores, chaves interruptoras e aparelhos medidores.
Desse modo, podemos realizar explorações e experimentos simulados
com circuitos elétricos. Ao abrir o simulador surge uma tela azul dentro
da qual existe um retângulo branco situado a sua direita.
6
O aviso “pegue um fio” também aparece, indicando a primeira ação a
ser executada. Para pegar fios e outros elementos disponíveis dentro do
retângulo branco, clique no elemento escolhido e arraste-o para a área
de trabalho azul.
No canto superior direito da área azul existe o botão Miscelânea. Esse
botão permite escolher objetos do cotidiano que também podem ser
inseridos no circuito permitindo ou não a circulação de corrente e o funcionamento dos outros elementos (FIG. 1)
Nas extremidades dos elementos inseridos na área de trabalho surgem
alças pontilhadas. Clicando sobre as alças que aparecem nas extremidades de um fio de ligação, podemos alterar o comprimento do fio e a
direção que ele ocupa no interior da área azul.
Também é possível mudar a orientação espacial das lâmpadas ao clicar com o botão esquerdo do mouse em um dos círculos tracejados e
vermelhos que indicam suas extremidades. Com o clique, aparece um
círculo amarelo e contínuo em volta do círculo vermelho. Girando e arrastando o mouse sobre esse círculo amarelo, fazemos a lâmpada girar
sobre si mesma.
FIG. 1 - Possibilidades do aplicativo
Unindo a alça que aparece na extremidade de um elemento qualquer com
outra alça situada na extremidade de outro elemento, ligamos dois elementos entre si. Para desconectar elementos recém-ligados é necessário
clicar com o botão direito no círculo que os une e selecionar a opção
“separar contato” (FIG. 2)
FIG. 2 - Visualização da opção “Separar contato”
É possível arrastar os elementos para a posição que quisermos. Além
disso, caso você se arrependa de ter escolhido um determinado elemento, basta clicar com o botão direito do mouse sobre o mesmo e escolher
a opção remover.
O botão direito do mouse também serve para alterarmos as propriedades
dos elementos de circuito, com exceção do fio de ligação e do interruptor.
No caso da bateria, o botão direito nos dá acesso às opções:
(i) Alterar a voltagem: com essa opção aumentamos ou diminuímos a
diferença na concentração de cargas elétricas negativas e positivas que
a bateria estabelece entre suas extremidades;
(ii) Alterar a resistência interna: com essa opção simulamos o envelhecimento de uma bateria, pois, quanto mais velha uma bateria, maior a
dificuldade apresentada para o transporte de cargas elétricas no interior
da mesma.
(iii) Reverter: com essa opção invertemos a posição dos polos da bateria.
as simulações que usaremos nas atividades a seguir, é totalmente gratuito, seguro e pouco exigente em termos de memória e capacidade de
processamento do computador.
Atividade 1 - Explorações iniciais
Um bom modo de aprender eletricidade é montar circuitos simples e explorar suas características. Quando lidamos com circuitos reais, a dica
é trabalhar com fontes de baixa tensão como pilhas ou baterias, já que
há riscos em manipular sem cuidado fontes de tensão maiores. Quando
lidamos com simulações, obviamente, não estamos sujeitos a riscos, nem
pessoais, nem de promover danos aos equipamentos. As explorações
reunidas nesta primeira atividade permitirão que você compreenda alguns
aspectos fundamentais dos circuitos e algumas das ideias e modelos que
utilizamos para compreendê-los.
Exploração 1.1 – Ligando uma lâmpada a uma bateria
1) Observando as instruções e as questões a seguir, utilize os elementos
de circuito presentes na simulação para fazer uma lâmpada incandescer
e emitir luz:
a) Ao levar uma lâmpada para a área de trabalho azul, note que há
dois terminais salientes na mesma, destacados por círculos tracejados e
vermelhos (FIG. 3).
FIG. 3 - Lâmpada e fios
7
b) Conecte um dos terminais da lâmpada a um dos terminais de uma
bateria.
c) Insira dois pedaços de fio na área de trabalho e una suas extremidades, de modo a formar uma espécie de V (FIG. 3).
d) Com o fio que acaba de montar, conecte o outro terminal da lâmpada ao segundo terminal da bateria e descreva as alterações observadas na aparência do circuito. Você compreende todos os símbolos que
aparecem nessa nova circunstância? Explique.
e) A lâmpada acesa está continuamente emitindo energia térmica (radiação infravermelha) e energia luminosa (radiação visível). De onde vem
essa energia? Como essa energia chega à lâmpada?
f) O que acontece com a aparência da simulação quando interrompemos o circuito ao clicar com o botão direito do mouse sobre um contato
qualquer que faz a conexão entre dois dos vários elementos do circuito?
8
Admitimos hoje que os materiais são feitos de átomos e que os átomos
são compostos por partículas mais externas que podem abandonar os
átomos a que estavam originalmente ligadas, em algumas situações. Essas partículas são chamadas elétrons e a circulação de elétrons em um
circuito dá origem a um fluxo conhecido como corrente elétrica.
Podemos entender o conceito de fluxo de cargas elétricas em um circuito
fazendo uma analogia entre a circulação de elétrons em um circuito elétrico e a circulação de água em um circuito de água. O fluxo de água que
sai de uma torneira é medido em litros por segundo. De forma semelhante, o fluxo de elétrons que emerge do polo negativo de uma pilha pode
ser medido em Coulombs por segundo (FIG. 4).
2) Agora, desconecte o fio, a bateria e a lâmpada e crie um modo de
religar esses três elementos de circuito, de tal forma que a lâmpada não
brilhe mais. Nessas circunstâncias, por que a simulação indica que a
bateria superaquece e queima?
3) Parta de um circuito aberto e tente religá-lo com vários tipos de objetos disponíveis na função Miscelânea (borracha, lápis, moeda etc.) que
aparece no canto superior direito da área de trabalho azul.
a) Com quais materiais conseguimos acender a lâmpada?
b) Talvez você já tenha ouvido falar dos termos condutores e isolantes
elétricos. Procure relacionar esses termos com os objetos que permitiram
ou não a passagem da corrente elétrica.
Exploração 1.2 – Inserindo um medidor de corrente elétrica no circuito
Quando ligamos os polos de uma fonte de energia elétrica através de
elementos condutores como fios ou filamentos metálicos de lâmpadas,
permitimos a circulação de cargas elétricas de um dos polos da fonte ao
outro e criamos um circuito elétrico. Na simulação que estamos utilizando,
a circulação de cargas elétricas é indicada por meio de grandes bolas
azuis que se movem pelo circuito.
FIG. 4 - Fluxo de elétrons
Assim como um litro de água corresponde a um número gigantesco de
moléculas de água, 1 Coulomb de elétrons corresponde a um número
muito grande de elétrons: 6,25 x 1018. Esse número, expresso em palavras, equivale a um valor superior a 6 bilhões de bilhões de elétrons!
Não é difícil reconhecer a dificuldade de se medir o fluxo de carga elétrica
em um circuito contando o número de elétrons que passa por um determinado ponto do circuito. Em virtude desta dificuldade, a corrente elétrica
é sempre medida de forma indireta.
amarelo e girar o mouse para fazer a lâmpada girar também; (ii) clicar
com o botão direito do mouse sobre o ícone da lâmpada e escolher a
função “Mostrar Conexão à Esquerda”.
A unidade 1 Coulomb/segundo é o padrão de medida de corrente elétrica. Tal unidade é chamada Ampére, em homenagem a um dos físicos
que mais contribuiu para o estudo e a compreensão do funcionamento
dos circuitos elétricos. Para aprender a medir a corrente elétrica de um
circuito construído por meio da simulação que estamos a utilizar, siga as
instruções:
• No lado direito da tela aberta pelo programa existe um retângulo verde com diversas funções. Nesse retângulo, na seção Ferramentas, temos
a opção de selecionar um amperímetro que pode ser, posteriormente, inserido no circuito. Para conectar o amperímetro ao circuito, devemos abrir
o circuito no ponto cuja corrente elétrica pretendemos medir, fechando
novamente o circuito através do amperímetro. Se for necessário, utilize
novos pedaços de fio para deixar seu circuito com uma boa aparência.
• Experimente conectar o amperímetro em pontos diferentes do circuito e responda: a posição ocupada por esse medidor altera o valor
da medida da corrente elétrica, feita em Amperes? Você esperava esse
resultado? Explique.
Exploração 1.3 – Ligando uma segunda lâmpada ao circuito
Monte um novo circuito para ligar duas lâmpadas ao fio e à bateria que
você usou na exploração anterior, mas mantenha funcionando o circuito
com apenas uma lâmpada ligada à bateria.
Para montar o novo circuito com as duas lâmpadas será preciso repetir
os procedimentos realizados na exploração 1, de modo a colocar novos
componentes na área de trabalho azul. Inseridos os novos componentes,
você deverá conectar um dos terminais de cada lâmpada a um cada dos
polos da bateria. O fio de ligação será, então, utilizado para conectar os
outros terminais das lâmpadas entre si (FIG. 5).
Para obter um resultado similar ao mostrado na Figura 5, você dever usar
dois artifícios: (i) clicar em um dos terminais da lâmpada até ele ficar
9
FIG. 5 - Conexões
a) Encontre duas maneiras diferentes de acender as duas lâmpadas
nessas condições. Essas duas ligações correspondem ao que denominamos um Circuito em Série.
b) Observe o brilho de cada uma das duas lâmpadas ligadas em série e compare-o ao brilho apresentado pela lâmpada ligada a um circuito
simples.
c) Ligue um amperímetro ao circuito com duas lâmpadas em série e
compare o valor da corrente elétrica com o valor estabelecido no circuito
simples (FIG. 6). A diferença entre as correntes estabelecidas nesses
dois circuitos é coerente com a diferença no brilho apresentado pelas
lâmpadas ligadas nos dois circuitos?
Atividade 2 - Simulando
circuitos com ligações entre
lâmpadas idênticas
Nesta atividade, temos a intenção de comparar a ligação de lâmpadas
em série, já utilizada na Exploração 3 da Atividade 1, com outro tipo de
associação entre aparelhos consumidores de energia elétrica: a ligação
em paralelo.
Procedimentos e questões:
1
0
FIG. 6 - Valor da corrente elétrica
d) Tente explicar o que ocorreu com o valor da corrente na ligação
da segunda lâmpada em série a partir das seguintes informações: todo
material condutor, como o filamento de uma lâmpada, por exemplo, opõe
certa dificuldade para a passagem da corrente elétrica em seu interior.
Essa dificuldade pode ser medida por meio de uma grandeza conhecida
como resistência elétrica.
1) Monte um circuito simples com uma lâmpada ligada a uma bateria por
meio de fios de ligação. Acrescente uma segunda lâmpada idêntica ligada
em série com a primeira e responda: a resistência elétrica total, exibida
pelo circuito como um todo, aumenta ou diminui quanto acrescentamos
uma segunda lâmpada em série com a primeira? Para responder, insira
um amperímetro no circuito conectado com um dos polos da bateria e
observe a medida de corrente elétrica quando há apenas uma lâmpada
no circuito ou quando há duas lâmpadas ligadas em série.
2) Dois elementos capazes de converter a energia elétrica proveniente
de uma fonte, em outras formas de energia, podem ser ligados de dois
modos distintos: em série ou em paralelo. Em um circuito com duas lâmpadas em série, quando uma lâmpada é desconectada, a outra automaticamente se apaga. Em um circuito em paralelo, quando uma lâmpada
é desconectada, a outra não é afetada. Monte um circuito com duas
lâmpadas em série e outro com duas lâmpadas em paralelo. Feito isso,
veja se o comportamento que acabamos de atribuir a esses dois tipos de
circuito realmente se verifica. Lembre-se de que você pode desconectar
as lâmpadas clicando com o botão direito na “alça” que liga qualquer um
dos terminais das lâmpadas aos fios de ligação.
3) Partindo do circuito com duas lâmpadas ligadas em série, acrescente
uma terceira e, depois, uma quarta lâmpada também ligada em série com
as demais: o que acontece com a corrente elétrica que sai da bateria e
com a resistência elétrica oferecida pelo circuito como um todo?
4) Volte agora ao circuito com duas lâmpadas em série. Acrescente uma
terceira lâmpada em paralelo com a segunda lâmpada e observe o que
acontece com o brilho da primeira lâmpada.
a) O que aconteceu com a corrente elétrica que sai da bateria?
b) De acordo com o que você observou, no item anterior, a resistência
elétrica do circuito aumenta ou diminui quanto acrescentamos uma lâmpada em paralelo com outra?
5) Volte agora ao circuito com duas lâmpadas em paralelo. Preveja o
que aconteceria com a corrente elétrica que sai da bateria, caso acrescentemos outras lâmpadas em paralelo nesse circuito. Faça isso, observe
o que acontece e registre suas hipóteses para explicar o que observou.
Atividade 3 - Chaves interruptoras e curtos-circuitos
Nesta atividade, pretendemos avançar nossa compreensão acerca do
conceito de resistência elétrica, ao inserir elementos de resistência desprezível em circuitos que contém resistores formados por filamentos de
lâmpadas.
Exploração 3.1 – Uso de chaves interruptoras
Na simulação que estamos utilizando, podemos inserir chaves interruptoras que podem ser ligadas ou desligadas a qualquer momento. Clicando com o botão esquerdo do mouse sobre a parte superior da chave e
arrastando o mouse para baixo podemos ligar as chaves. Para desligar
esse tipo de chave é preciso clicar sobre o ícone da chave, de modo a
fazer surgir um retângulo amarelo sobre a mesma; clicando sobre esse
retângulo e arrastando o mouse para cima, a chave pode ser desligada.
Seguindo essas instruções, introduza uma chave interruptora em um circuito montado com uma pilha e duas lâmpadas ligadas em paralelo, de
modo que a chave interruptora possa ser usada para:
(i) Ligar e desligar apenas uma das duas lâmpadas;
(ii) Ligar e desligar simultaneamente as duas lâmpadas.
Exploração 3.2 – Curto-circuito em uma lâmpada
1) A Figura 7 apresenta um circuito contendo duas lâmpadas ligadas em
série. Note a presença de uma chave interruptora na parte mais alta do
circuito.
a) Preveja o que acontecerá com o brilho das duas lâmpadas quando
a chave for ligada.
b) Monte o circuito ilustrado na figura e descreva o que acontece com
a corrente elétrica indicada pelo amperímetro.
c) Interprete esse fenômeno em termos da resistência total oferecida
pelo circuito diante da polaridade estabelecida pela fonte de tensão.
1
1
FIG. 8 - Circuito com três lâmpadas em série
1
2
FIG. 7 - Circuito com duas lâmpadas em série
2) A Figura 8 apresenta um circuito com três lâmpadas em série. Note
que uma das lâmpadas foi ligada em paralelo com um trecho de circuito
que contém uma chave interruptora aberta. Monte um circuito como esse
no seu simulador. Note que, para o circuito funcionar, você deve fechar
o interruptor situado na parte inferior do circuito, entre a bateria e o amperímetro.
a) Depois que a chave interruptora situada na parte inferior do circuito
estiver ligada e circuito estiver funcionando, experimente ligar a chave
interruptora colocada na parte superior do circuito, em paralelo com uma
das lâmpadas. Isso fará com que essa lâmpada seja curto-circuitada.
b) Descreva o que acontece com o brilho das três lâmpadas e com
a corrente elétrica indicada pelo amperímetro. Interprete esse fenômeno
em termos da resistência total oferecida pelo circuito diante da polaridade
estabelecida pela fonte de tensão.
Exploração 3.3 – Curto-circuito total
A figura a seguir apresenta um circuito com três lâmpadas ligadas em
paralelo. Note que para o circuito funcionar, você deve fechar o interruptor
situado na parte inferior do circuito, entre a bateria e o amperímetro. Note,
ainda, que na parte superior do circuito existe uma chave interruptora
aberta, que está ligada em paralelo com as três lâmpadas. Depois que
a chave situada na parte inferior estiver fechada, experimente ligar, também, a chave interruptora situada na parte superior do circuito. Observe
atentamente todas as informações que se tornarão disponíveis na área de
trabalho. Interprete esse fenômeno em termos da resistência total oferecida pelo circuito diante da polaridade estabelecida pela fonte de tensão.
Atividade 4 – Resistência de
condutores metálicos e de
associações de resistores
Os metais estão entre os melhores condutores de corrente elétrica disponíveis. Entretanto, ser bom condutor não significa não oferecer resistência à passagem da corrente elétrica. Todos os materiais, a temperatura
ambiente, oferecem certa resistência elétrica. Além da temperatura, essa
resistência depende de certo conjunto de fatores, cujo conhecimento e
controle são essenciais na concepção dos circuitos elétricos.
Nesta atividade, além de continuar usando a simulação explorada nas atividades anteriores, nós também usaremos o aplicativo Resistência em um
condutor (resistance-in-a-wire_pt.jar) que está disponível no endereço
eletrônico http://phet.colorado.edu/en/simulations/translated/pt. O uso
simultâneo dos dois aplicativos nos permitirá investigar como a resistência
elétrica oferecida por um fio condutor metálico depende de características
do fio e da temperatura na qual ele se encontra.
Os filamentos das lâmpadas incandescentes, embora não pareçam, são
feitos a partir de um fio condutor cilíndrico que é enrolado em espiral. A
espiral assim formada é novamente enrolada em outra espiral. Com essa
estratégia, consegue-se fazer com que um fio muito longo e fino fique
totalmente contido no pequeno espaço reservado aos filamentos nas lâmpadas incandescentes. O fato de que os filamentos são constituídos por
fios cilíndricos é o que nos permite utilizar o aplicativo Resistência em um
condutor para extrair conclusões sobre a resistência oferecida tanto pelos
filamentos das lâmpadas, quanto pelos fios de ligação que compõem os
circuitos.
Exploração 4.1 – Resistência equivalente de uma associação de resistores em série
A resistência elétrica é uma grandeza destinada a identificar a dificuldade
oferecida por um elemento de circuito à passagem da corrente elétrica.
Tal grandeza é medida por meio de uma unidade conhecida como Ohm
(símbolo Ω). Essa medida, tanto pode ser utilizada para caracterizar elementos de circuito isolado, quanto para identificar o comportamento de
um circuito como um todo. Para compreender esse aspecto importante do
conceito de resistência, faça o que se pede a seguir.
Utilize o aplicativo em Java Circuit Construction Kit DC para montar um
circuito simples, com apenas uma lâmpada, ao lado de um circuito que
contém duas lâmpadas ligadas em série.
Insira amperímetros nos dois circuitos, de modo a medir as correntes elétricas que entram ou saem das fontes de tensão neles inseridas.
Feito isso, altere a resistência elétrica da lâmpada inserida no circuito
simples, da seguinte forma:
(i) Clique com o botão direito do mouse sobre o ícone que representa
a lâmpada e escolha a opção Alterar Resistência;
(ii) Uma caixa com um botão deslizante aparecerá e permitirá alterar
a resistência da lâmpada;
(iii) Observe o valor da corrente elétrica que é exibido pelo amperímetro
conectado ao circuito simples e altere a resistência da lâmpada até que a
corrente no circuito simples coincida com a corrente no circuito com duas
lâmpadas em série.
a) Quantos ohms de resistência apresenta a lâmpada inserida no circuito simples, quando a corrente nesse circuito se iguala àquela estabelecida
no circuito com as duas lâmpadas associadas em série?
b) Clique com o botão direito em cada uma das duas lâmpadas ligadas
em série e acione a função Alterar Resistência apenas para descobrir qual
é a resistência elétrica de cada uma delas. A soma dessas resistências
possui alguma relação com a resistência apresentada pela lâmpada no
circuito simples?
1
3
c) Seria apropriado dizer que a resistência apresentada pelo filamento
da lâmpada inserida no circuito simples, após ser alterada, tornou-se
equivalente à resistência apresentada pela associação das duas lâmpadas em série?
Exploração 4.2 – Resistência equivalente de uma associação de resistores em paralelo
Quando associamos resistores em série, tal como no caso do circuito
montado na exploração 1, nós aumentamos a resistência equivalente do
circuito e reduzimos a corrente que entra ou sai da fonte de tensão. Mas,
e quando associamos resistores (ou lâmpadas) em paralelo?
1
4
Nesse caso, embora a resistência elétrica de cada elemento individual
continue a ser uma medida da dificuldade oferecida por esse elemento à passagem da corrente elétrica, temos de considerar que a ligação
de novos elementos, em paralelo, aumenta o número de caminhos que
permitem a passagem de corrente no circuito como um todo. Em outras
palavras, a associação de novos resistores (ou filamentos) em paralelo
aumenta a facilidade de circulação de corrente pelo circuito como um
todo e, por isso, diminui a resistência oferecida por essa associação.
Para explorar essa característica importante das associações de resistores em paralelo, faça o que se pede a seguir.
Utilize o aplicativo em Java Circuit Construction Kit DC para montar um
circuito simples, com apenas uma lâmpada, ao lado de um circuito que
contém duas lâmpadas ligadas em paralelo.
Insira amperímetros nos dois circuitos, de modo a medir as correntes
elétricas que entram ou saem das fontes de tensão neles inseridas.
Feito isso, altere a resistência elétrica da lâmpada inserida no circuito
simples até que o valor da corrente elétrica no amperímetro conectado ao
circuito simples se iguale à corrente no circuito com duas lâmpadas em
paralelo. Note que, além do botão deslizante, você poderá digitar diretamente valores de resistência elétrica na caixa que se abre quando você
utiliza a função Alterar Resistência.
a) Quantos ohms de resistência apresenta a lâmpada inserida no circuito simples, quando a corrente nesse circuito se iguala àquela estabelecida
no circuito com as duas lâmpadas associadas em paralelo?
b) Clique com o botão direito em cada uma das duas lâmpadas ligadas
em paralelo e acione a função Alterar Resistência apenas para descobrir
qual é a resistência elétrica de cada uma delas. Como se comparam a
resistência de cada lâmpada individual e a resistência da lâmpada colocada no circuito simples?
c) Seria apropriado dizer que a resistência apresentada pelo filamento da lâmpada inserida no circuito simples, após ser alterada, tornou-se
equivalente à resistência apresentada pela associação das duas lâmpadas
em paralelo?
Exploração 4.3 – Alterações nos filamentos e mudanças na resistência
das lâmpadas
Nas explorações 1 e 2, nós promovemos alterações na resistência dos
filamentos das lâmpadas sem enxergar as eventuais mudanças nas características dos filamentos que poderiam explicar tais alterações. Nesta
exploração nós poderemos utilizar o aplicativo Resistência em um condutor para compreender como alterar as características do filamento de uma
lâmpada para promover mudanças em sua resistência. O uso desse aplicativo pressupõe a compreensão dos símbolos que ele reúne e apresenta.
A Figura 9 foi gerada a partir de uma captura da tela da interface do
aplicativo e nos ajudará a alcançar tal compreensão. Na parte inferior
da imagem aparece a ilustração de um fio condutor metálico e cilíndrico,
cujas características podem ser alteradas com o acesso aos botões deslizantes que aparecem no lado direito da interface do aplicativo. Na parte
superior da imagem, no lado esquerdo, temos a apresentação do valor da
resistência do fio, dada em ohms (1,35 ohm, na imagem que capturamos
e apresentamos na figura 9). Logo abaixo dessa informação, vemos uma
equação que relaciona o valor da resistência elétrica (R) com as características que determinam essa resistência:
ρ (resistividade): A resistividade é uma característica que identifica, tanto
o tipo de material utilizado na confecção do fio, quanto a temperatura que
O tipo de material é um fator importante
porque materiais diferentes apresentam
diferentes tipos de organização microscópica para seus átomos. Assim, por
exemplo, a organização microscópica
dos átomos em objetos feitos de alumínio (Al) possui a geometria mostrada
na figura ao lado. No lado direito dessa
figura, as bolinhas de cor cinza identificam átomos situados em segundo plano. Esse tipo de geometria é denominada cúbica de face centrada. As
geometrias características de outros metais podem ser obtidas na internet.
Nesse caso, a área de seção transversal A será a área da superfície de uma fatia do salame, que poderia ser medida, por
exemplo, em centímetros quadrados (cm2). A área de seção
transversal é um parâmetro importante para a determinação da
resistência elétrica, porque um aumento dessa área torna mais
fácil o fluxo de cargas elétricas através do fio. Como facilidade
e dificuldade são qualidades opostas, isso equivale a dizer que
quanto maior o valor da seção transversal A de um fio, menor
será a resistência elétrica R apresentada por esse fio.
Alguns tipos de organização microscópica facilitam o fluxo de cargas elétricas no interior do fio, enquanto outros contribuem para esse fluxo seja
mais restrito. Na simulação, devido à impossibilidade de representar os
átomos e sua forma de organização, foram utilizados pontinhos pretos
cuja concentração sugere o aumento ou a diminuição da resistividade do
fio metálico.
1
5
L (comprimento): O comprimento do fio que apresenta resistência elétrica
interfere diretamente no valor da resistência. Na exploração 1, constatamos que a associação de filamentos em série, aumenta a resistência
equivalente do circuito. Considerando dois filamentos idênticos, podemos
interpretar esse fato racionando do seguinte modo: dois filamentos (ou
resistores) idênticos, associados em série, apresentam uma resistência
igual àquela apresentada por um único filamento de mesmo material e
espessura, mas com o dobro do comprimento dos filamentos individuais.
Esse fato aparece na equação como uma relação de proporcionalidade
entre resistência (R) e comprimento (L).
A (área de seção transversal): O parâmetro A identifica a área de seção
transversal, uma medida que nos permite identificar, indiretamente, o diâmetro de um fio. Para compreender o significado dessa medida, veja a
figura ao lado e imagine que ela representa um cilindro feito de salame.
FIG. 9 - Fio condutor metálico e cilíndrico
Levando em consideração todas essas informações, faça o que se pede
a seguir:
1
6
a) No aplicativo, manipule os botões deslizantes para variar a resistência elétrica do fio em função dos parâmetros descritos acima. Ao fazer
isso, observe, atentamente, as mudanças: (i) no valor da resistência do
fio que é dado em ohm; (ii) no tamanho das letras que representam os
parâmetros ρ, L e A inseridos na equação; (iii) nas características visuais
do fio representado na parte inferior da tela. Você diria que todas essas
mudanças são coerentes com as informações que apresentamos acima
sobre a importância dos parâmetros ρ , L e A na determinação da resistência elétrica de um fio?
b) Utilize o aplicativo para reproduzir os valores das resistências das
lâmpadas inseridas nos circuitos simples, equivalentes às resistências
das associações de resistores que você construiu nas explorações 1 e 2.
Descreva, então, as alterações que tiveram de ser produzidas nos filamentos das lâmpadas inseridas nos circuitos simples, de modo a alterar
a resistência que essas lâmpadas apresentavam inicialmente.
c) Analise atentamente as novas informações apresentadas a seguir,
em itálico, antes de prosseguir explorando a simulação: No item anterior,
você teve a liberdade de alterar quaisquer dos parâmetros L , ρ e A
para obter as resistências das lâmpadas inseridas nos circuitos simples,
equivalentes às resistências das associações de resistores que você
construiu nas explorações 1 e 2. Os filamentos das lâmpadas
incandescentes reais, porém, são sempre produzidos a partir de uma
mesma liga metálica: o tungstênio. Por isso, o parâmetro ρ, ou seja, a
resistividade do fio que compõem o filamento, não pode variar a nosso
bel prazer. A temperatura do filamento de uma lâmpada incandescente
varia muito, dependendo do circuito no qual a lâmpada está ligada e
do brilho que ela apresenta. Desse modo, como a resistividade é muito
afetada pela temperatura, não é possível definir um valor fixo para a
resistividade do tungstênio nos circuitos construídos virtualmente nas
explorações 1 e 2.
d) Apesar das dificuldades apresentadas no texto acima, em negrito,
vale a pena deslizar o botão da resistividade no aplicativo para sua posição de máximo (1,01 Ω.cm) e fixar esse valor momentaneamente para
fazer o que se pede a seguir. Volte a utilizar o aplicativo para reproduzir a alteração imposta ao valor da resistência da lâmpada inserida no
circuito simples construído na exploração 1, quando essa resistência foi
alterada desde o valor inicial, até o valor que corresponde à resistência
equivalente da associação dos filamentos em série. Desta vez, porém,
mantenha fixas, tanto a resistividade, quanto a área de seção transversal
do fio. O que esse procedimento nos revela em termos da relação entre
o comprimento do fio e a resistência que ele apresenta?
e) Utilize, uma última vez, o aplicativo para reproduzir a alteração
imposta ao valor da resistência da lâmpada inserida no circuito simples
construído na exploração 2, quando essa resistência foi alterada desde
o valor inicial, até o valor que corresponde à resistência equivalente da
associação dos filamentos em paralelo. Desta vez, porém, mantenha fixas,
tanto a resistividade, quanto o comprimento do fio. O que esse procedimento nos revela em termos da relação entre a área de seção transversal
do fio e a resistência que ele apresenta?
f) Avalie as duas sequências de imagens apresentadas na Figura 10,
de modo a identificar qual delas representa um modo de obter uma resistência equivalente a duas resistências associadas: (i) em série; (ii) em
paralelo. Analise se essas imagens sugerem processos coerentes com as
explorações que fizemos nos itens anteriores desta atividade.
+
=
=
+
FIG. 10 - Resistências
=
Atividade 5 - Voltagem como
medida da tensão e da
diferença de potencial elétrica
Esta é uma atividade de leitura que foi concebida para apresentar os
vários aspectos de uma medida conhecida como voltagem. Tal medida,
como se verá mais adiante, é útil tanto para caracterizar as fontes de
energia elétrica, quanto para investigar como a energia elétrica é distribuída ao longo de um circuito. Na primeira seção desta atividade, ocupamo-nos, centralmente, do conceito de polaridade e de tensão elétrica. Na
segunda seção, definimos a unidade de medida de tensão elétrica. Na
terceira seção, apresentamos uma analogia entre circuitos hidráulicos e
elétricos. A importância de tal analogia será notada na quarta seção, na
qual apresentaremos considerações sobre os processos de transformação
e transferência de energia em um circuito elétrico. Nessa ocasião, você
terá a oportunidade de utilizar o simulador de circuitos para fazer medidas
de voltagem que o ajudarão a avaliar e a compreender as afirmações
feitas no texto.
5.1 - Polaridade e tensão elétrica como recursos para a caracterização
de fontes de energia
Na lateral das pilhas encontramos o número 1,5 V. A unidade representada pela letra V é o Volt. Mas o que é exatamente 1 Volt? O que significa
o termo voltagem?
Volt é o nome de uma unidade de medida que caracteriza as fontes de
energia elétrica. Esse tipo de fonte consiste em um dispositivo capaz de
estabelecer uma polaridade entre dois pontos de um circuito elétrico. Um
desses pontos deve apresentar excesso de carga negativa em relação ao
outro. Estabelece-se, assim, um polo negativo e outro positivo que irão
provocar a circulação de corrente elétrica no circuito.
Pode-se imaginar que o excesso de cargas negativas existente no polo
negativo repele os elétrons dos materiais condutores que têm mobilidade
(elétrons “livres”), ao mesmo tempo em que o excesso de cargas positivas existentes no polo positivo atrai os mesmos elétrons. A ação simultânea de forças elétricas atrativas e repulsivas no interior dos materiais
que compõem o circuito é a causa do fluxo de cargas elétricas a que
chamamos corrente elétrica.
O primeiro sentido importante a que devemos associar, tanto a unidade
de medida 1 Volt, quanto a palavra voltagem é o conceito de polaridade
elétrica. A palavra voltagem é derivada do termo volt e não possui outro
significado além desse. Outras palavras usadas para designar a medida
da polaridade estabelecida por uma fonte de energia elétrica, que é realizada em volts, são tensão elétrica e diferença de potencial ou d.d.p.
Os dicionários de português brasileiro nos dizem que tensão é a qualidade
ou estado do que é tenso, enquanto tenso é tudo aquilo que é estendido
com força, esticado, retesado. Essa conceituação tem origem nos conceitos de tensão e força mecânicas. Mas a tensão elétrica também envolve
a ideia de força, já que é necessária a ação de uma força elétrica para:
(i) retirar elétrons de um ponto do circuito, transformando esse ponto em
um polo positivo; (ii) inserir esses mesmos elétrons em outro ponto do
circuito, transformando-o em um polo negativo.
As ideias de tensão e força estão, por sua vez, associadas à ideia de
energia potencial (ou energia armazenada). Assim, por exemplo, um arco
prestes a lançar uma flecha encontra-se tensionado. Esse estado de
tensão dota o sistema arco + flecha de uma energia potencial elástica.
Quando o arco é abandonado e volta a sua forma original, a energia desse sistema é transformada em energia de movimento da flecha.
Quando uma fonte de energia elétrica estabelece uma polaridade em dois
pontos de um circuito, ela também dota o sistema fonte + elementos de
ligação + aparelho consumidor de uma energia potencial elétrica. Com o
circuito ligado, essa energia se transforma em outras formas de energia.
1
7
Caso o circuito contenha uma lâmpada ligada à fonte de tensão, a transformação de energia envolverá a “produção” de calor e luz.
Para manter excessos de carga elétrica positiva e negativa nas extremidades do circuito uma fonte de tensão pode recorrer a reações químicas.
Esse é o caso das pilhas e baterias. Outra possibilidade é a de estabelecer polos opostos a partir de forças de origem eletromagnética agindo
sobre os elétrons livres de uma bobina feita a partir de um fio metálico
enrolado em torno de um núcleo. Esse é o caso dos geradores de uma
usina hidrelétrica, cuja estrutura e funcionamento não são abordados
neste livro.
1
8
Para manter uma diferença de polaridade entre as extremidades de um
circuito elétrico, uma fonte de tensão deve necessariamente promover
transformações de energia. Baterias e pilhas utilizam energia liberada em
reações químicas. Geradores de usinas hidrelétricas usam a energia de
movimento de quedas d’água.
5.2 - Como se define a unidade de medida da tensão elétrica
Quando mantém a polaridade em um circuito em funcionamento, uma
fonte de tensão realiza o trabalho de deslocar cargas elétricas de uma
extremidade do circuito à outra. A unidade Volt expressa a quantidade de
energia que a fonte utiliza para deslocar elétrons em seu interior, de tal
forma a manter a polaridade entre as extremidades do circuito. Considerando o Joule como unidade de medida de energia e o Coulomb como
unidade de medida de carga, teremos a seguinte definição para o Volt:
para deslocar 1 Coulomb de elétrons entre os terminais da fonte. Quando
a polaridade é muito superior a 1 Volt, existe uma maior diferença na concentração de cargas elétricas presentes nos dois polos. Sendo assim, uma
quantidade muito maior de energia é necessária para deslocar 1 Coulomb
de elétrons de um polo a outro!
Do que acabamos de dizer, podemos concluir que a voltagem é uma medida indireta da polaridade estabelecida por uma fonte de tensão elétrica.
Já que não é nada prático contar o número de elétrons que são transferidos de um polo a outro no ato de criação da polaridade, passa-se a
medir a energia necessária para manter a polaridade.
5.3 - Uma analogia entre pressão hidráulica e tensão elétrica
Uma analogia entre um circuito hidráulico e um circuito elétrico pode contribuir para o entendimento do conceito de tensão elétrica. Apesar das
diferenças óbvias, existem semelhanças entre circuitos hidráulicos e elétricos que auxiliam a compreensão de ambos. Compare as duas figuras
apresentadas a seguir para acompanhar a analogia que foi estruturada a
partir das afirmações 1 a 7 enumeradas após a Figura 111.
1 Volt = 1 Joule/Coulomb
O Joule é uma unidade de medida da energia relativamente pequena.
Um Joule (1 J) equivale à energia necessária para erguer uma massa
de apenas 98 gramas a uma altura de 1 metro acima do nível do mar.
Um Coulomb, por outro lado, equivale a uma grande quantidade de
elétrons. Assim, dizemos que uma fonte de tensão apresenta 1 Volt de
diferença de potencial quando é necessário apenas 1 Joule de energia
FIG. 11 - Circuito hidráulico e Circuito Elétrico
1. Uma fonte de energia é necessária para estabelecer um fluxo no
interior de ambos os circuitos: bomba d’água no caso hidráulico (Figura
11, na esquerda) e bateria no caso elétrico (Figura 11, na direita).
2. Nem a água, nem as cargas elétricas são criadas ou perdidas dentro
de cada circuito.
3. Existem resistências aos dois fluxos: diâmetro dos tubos e presença
de conexões no caso hidráulico e filamentos de lâmpadas ou resistores
no caso elétrico.
4. A bomba d’água estabelece uma diferença de pressão entre os
pontos A e B do circuito hidráulico; a bateria estabelece uma tensão (polaridade) entre os pontos A e B do circuito elétrico.
5. Devido à diferença de pressão estabelecida entre os pontos A e B
do circuito hidráulico, a bomba d’água consegue elevar água até o reservatório I. Nesse processo, cada metro cúbico (m3) de água adquire energia potencial gravitacional. A altura máxima do reservatório I e a energia
potencial adquirida pela água serão proporcionais à diferença de pressão.
6. Para manter uma tensão elétrica entre os polos A e B do circuito
elétrico, a bateria precisa deslocar cargas elétricas, internamente, entre
seus terminais. Nesse processo, cada Coulomb de carga deslocado adquire energia potencial elétrica.
7. No circuito hidráulico, a energia potencial gravitacional de cada m3
de água é transformada em energia de movimento da água quando esse
material flui do reservatório I para o II. Essa energia é transferida para as
pás do moinho sendo novamente transformada, pelo moinho, em outras
formas de energia.
5.4 - Diferença de potencial em circuitos série e paralelo
Na primeira seção desta atividade de leitura, os conceitos de polaridade
e tensão elétrica foram apresentados como um recurso para a caracterização das fontes de energia elétrica. Posteriormente, na segunda seção,
afirmou-se que a tensão elétrica é medida em Volts e que a voltagem é
uma medida indireta da polaridade estabelecida por uma fonte de tensão
elétrica. Na terceira seção apresentou-se uma analogia entre circuitos
hidráulico e elétrico que será retomada mais adiante.
Note que no circuito à direita da Fig.1, a corrente elétrica foi representada no sentido
convencional. Nesse caso, supõe-se que a corrente envolva o fluxo de cargas
positivas pelo circuito. A partir do século XX, passou-se a imaginar que, nos
circuitos constituídos de elementos metálicos, a corrente elétrica está associada ao fluxo
de elétrons e, portanto, de cargas negativas. Ainda assim, o sentido convencional da
corrente ainda continua a ser adotado por razões que não serão apresentadas neste
livro.
5.4. A) Elevação e queda de potencial em um circuito em série
O circuito representado na Figura 12, à esquerda, mostra dois elementos
consumidores de energia de movimento (dois moinhos dotados de pás
giratórias) que estão ligados em série no circuito hidráulico. Na Figura 12,
à direita, vemos duas lâmpadas, e, portanto, dois elementos consumidores
de energia elétrica, ligadas também em série no circuito elétrico.
1
Nesta seção, vamos introduzir outro conceito intimamente ligado às ideias
de tensão elétrica e voltagem. Esse conceito, conhecido como diferença
de potencial (ddp), nos permite aplicar, na análise dos circuitos elétricos,
um dos princípios mais importantes das ciências: o princípio de conservação da energia. De acordo com esse princípio, em um sistema fechado,
a energia não pode ser criada ou destruída, mas apenas transformada ou
transferida.
Do princípio de conservação de energia podemos deduzir que a energia despendida pela fonte para manter a polaridade em seus terminais
deve ser, posteriormente, transferida e transformada em outras formas
de energia nos elementos que compõem um determinado circuito. Vamos
analisar aqui como ocorre essa transferência/transformação da energia
em circuitos que contêm duas lâmpadas idênticas ligadas, ora em série,
ora em paralelo.
Nesse caso, será interessante retomar a analogia entre circuitos hidráulico
e elétrico, que apresentamos na terceira seção desta atividade de leitura.
Até porque já iniciamos, naquela ocasião, a análise dos processos de
transferência/transformação de energia nesses dois tipos de circuito.
1
9
De modo similar ao que acontece no circuito hidráulico em série, afirmamos que no circuito elétrico em série, mostrado na figura da direita, ocorre
uma elevação de potencial elétrico entre os terminais A e B da bateria.
Essa elevação de potencial produzida pela fonte, identificada pelo símbolo VAB, permite que, posteriormente, ocorram transformações de energia
e “quedas de potencial” nos terminais dos dois aparelhos consumidores
desse circuito: as lâmpadas L1-2 e L3-4. Se chamarmos as quedas de potencial ocorridas nas lâmpadas como V12 e V34, podemos utilizar o princípio de conservação de energia para afirmar que: VAB = V12 +V34.
FIG. 12 - Moinhos de pás giratórias e lâmpadas em série
2
0
No circuito da esquerda, como já dissemos, a bomba fornece energia
potencial gravitacional a cada m3 de água deslocada para o reservatório
I, que é o ponto do circuito de potencial mais elevado, ou, em outras palavras, é o ponto do circuito no qual é maior a energia potencial gravitacional por m3 de água. Parte dessa energia potencial é transformada em
energia de movimento e transferida para as pás do moinho MI-II, situado
entre os reservatórios I e II.
O potencial gravitacional, ou a energia potencial gravitacional por m3 de
água, no reservatório II é menor que no reservatório I, mas maior que no
reservatório III. Sendo assim, quando a água flui do reservatório II para o
III, uma nova transformação de energia potencial gravitacional em energia
de movimento permite o funcionamento do moinho MII-III.
Por fim, quando atinge o reservatório III, a água apresenta seu menor
valor de energia potencial gravitacional, por m3, em todo o circuito. Dizemos, por isso, que o potencial desse reservatório é o menor de todo
o circuito e que a ação da bomba ao deslocar a água entre os reservatórios III e I consiste em elevar novamente o potencial gravitacional da
água, de modo a manter uma diferença de potencial capaz de permitir o
funcionamento contínuo do circuito.
Ao dar um exemplo numérico, no caso do circuito contar com uma bateria
de 12 Volts, e das duas lâmpadas utilizadas serem idênticas entre si, nós
podemos afirmar que:
12 Joules/C = 6,0 Joules/C (em L1) + 6,0 Joules/C (em L2)
(VAB)
(V12)
(V34)
Avalie, com o auxílio do simulador, as afirmações
que você acaba de ler sobre a tensão em circuitos
em série
Você pode utilizar o simulador de circuitos para reproduzir esses dados numéricos em um circuito de lâmpadas idênticas ligadas em série.
Para fazê-lo, observe que, no lado direito da tela aberta pelo programa, existe um retângulo verde com diversas funções. Nesse retângulo, na seção Ferramentas, temos a opção de selecionar um aparelho
conhecido como voltímetro que pode ser, posteriormente, inserido no
circuito. Para ligar o voltímetro ao circuito, devemos conectar suas
pontas de prova (um cabo preto e outro vermelho) nas extremidades
do elemento de circuito cuja voltagem nós pretendemos medir. Ligue
os cabos do voltímetro nos terminais da bateria para medir a voltagem
que ela estabelece nos terminais da associação de lâmpadas. Depois,
ligues os cabos do voltímetro nos terminais de cada uma das lâmpadas individualmente. E então: as medidas confirmam as afirmações
que fizemos no texto acima.
Em termos de uma interpretação microscópica acerca do que acontece no
interior desse circuito elétrico, podemos dizer que a energia potencial elétrica transferida pela fonte para cada Coulomb de carga transferida entre
seus terminais é transformada em energia de movimento de elétrons dos
átomos que compõem os materiais presentes no circuito. No interior dos
filamentos das lâmpadas, esses elétrons em movimento se chocam com
os átomos do filamento (modelo de Drude-Lorentz).
servatório II, o mais baixo do circuito.
Como as diferenças de potencial gravitacional entre os pontos 1 e 2 ou
entre os pontos 3 e 4 são idênticas, dizemos que os moinhos estão
submetidos a uma mesma diferença de potencial gravitacional, algo que,
em linguagem matemática, equivale a dizer que V12 = V34.= VAB (que é a
diferença de potencial entre os reservatórios I e II, mantida pela bomba
de água inserida no circuito).
Essas colisões transferem energia de movimento para os átomos que,
desse modo, aumentam seu grau de agitação térmica enquanto o filamento sofre uma grande elevação de temperatura. De tão quente, o filamento
emite calor e luz para o ambiente que os cerca transferindo a energia de
dentro para fora do circuito. Nesse processo, diz-se que a energia elétrica
foi transformada em energia térmica e em energia luminosa.
Note que a mesma análise poder ser realizada no circuito elétrico da
direita, no qual as lâmpadas L12 e L23 estão submetidas a diferenças de
potencial equivalentes. O potencial associado ao polo positivo, o ponto A
do circuito, é idêntico aos potenciais elétricos nos pontos 1 e 3 situados
no terminal da esquerda, respectivamente, das lâmpadas L12 e L34. Por
sua vez, o potencial associado ao polo negativo, o ponto B do circuito, é
também idêntico aos potenciais elétricos nos pontos 2 e 4 situados nos
terminais localizados no lado direito das duas lâmpadas. Tudo se passa
como se cada uma das lâmpadas estivesse ligada independentemente
aos polos da fonte de tensão. Para uma fonte de alta potência, no caso
de uma das duas lâmpadas ser retirada do circuito, nenhum efeito se verificará na outra lâmpada. Mais uma vez pode-se afirmar que V12 = V34=
VAB (que é a diferença de potencial entre os polos A e B, que é mantida
pela fonte de tensão inserida no circuito).
Algo importante a se dizer ao se considerar uma interpretação microscópica do fenômeno é que o ato de ligar o circuito estabelece, simultaneamente, nos dois filamentos ligados em série, as forças que provocarão
as colisões entre os elétrons e os átomos que compõem os filamentos.
Nesse caso, precisamos nos lembrar de que todos os materiais que
compõem os circuitos são constituídos por átomos e por seus respectivos
elétrons. Isso explica o fato de que a corrente elétrica em um circuito
em série é a mesma em todos os pontos do circuito, sendo iniciada ou
interrompida simultaneamente em todo o circuito quando ligamos ou desligamos o mesmo.
5.4.B) Elevação e queda de potencial em um circuito em paralelo
Os circuitos representados na Figura 13 a seguir apresentam elementos
consumidores de energia ligados em paralelo. No circuito da esquerda
temos 2 moinhos situados entre dois níveis de potencial. Um dos moinhos, denominado M12, está localizado entre os potenciais gravitacionais
1 e 2. O outro, identificado como M34, segue situado entre os potenciais
gravitacionais 3 e 4. Ao analisar essa figura é fácil constatar que os potenciais gravitacionais 1 e 3 são idênticos entre si e que coincidem com
o potencial do reservatório I, no alto do circuito. O mesmo acontece com
os potenciais gravitacionais 2 e 4 que coincidem com o potencial do re-
L 1-2
Reservatório
I
1
3
1
2
L 3-4
M1-2
A
Reservatório
II
B
(P AB >P )
M3-4
2
4
FIG. 13 - Moinhos de pás giratórias e lâmpadas
3
A
4
B
2
1
No caso de uma bateria de 12 Volts e de lâmpadas idênticas o número
de Joules por Coulomb fornecido pela bateria não se alterará, quando
comparado ao número que se verifica quando a mesma bateria estiver
ligada a apenas uma lâmpada. No entanto, o número de Coulombs que
atravessará a bateria será duas vezes superior ao número estabelecido
quando apenas uma lâmpada estiver ligada a essa fonte de tensão elétrica. Em outras palavras, a corrente total que passa pela fonte ligada a
duas lâmpadas idênticas conectadas em paralelo será duas vezes maior
que a corrente estabelecida quando apenas uma lâmpada está ligada ao
circuito.
2
2
Avalie, com o auxílio do simulador, as afirmações
que você acaba de ler sobre a tensão em circuitos
em paralelo
Você pode utilizar o simulador de circuitos para reproduzir esses
dados numéricos em um circuito de lâmpadas idênticas ligadas em
paralelo. Ligue os cabos do voltímetro nos terminais da bateria para
medir a voltagem que ela estabelece nos terminais da associação
de lâmpadas. Depois, ligues os cabos do voltímetro nos terminais de
cada uma das lâmpadas individualmente. E então: as medidas confirmam as afirmações que fizemos no texto acima?
Atividade 6 - Medidas de
tensão em um circuito elétrico
O objetivo desta atividade é propor a utilização dos conceitos de tensão
elétrica, voltagem e diferença de potencial para investigar o funcionamento
dos circuitos. Para isso: (i) observaremos associações de baterias em série ou em paralelo; (ii) mediremos a voltagem em associações de baterias
e em diferentes trechos de um circuito.
A medida da tensão ou da diferença de potencial em um trecho do
circuito pode ser realizada na simulação com o uso da função voltímetro.
Para acionar essa função, considere as informações que apresentamos
em um quadro inserido na seção 5.4.B (Elevação e queda de potencial
em um circuito em série) da atividade anterior (Voltagem como medida
da tensão e da diferença de potencial elétrica).
Exploração 6.1 - Associação de baterias
Existem, basicamente, dois tipos de associações entre pilhas: a associação em série e a associação em paralelo. A diferença fundamental entre
esses dois tipos de associação é a maneira como os polos das pilhas são
conectados entre si. As figuras apresentadas a seguir ilustram cada um
desses dois tipos de associação.
1) Para começar, monte um circuito elétrico com uma única bateria e uma
única lâmpada. Depois, orientando-se pela Figura 14 acrescente uma segunda bateria em série com a primeira (o circuito mostrado nessa figura
exibe uma chave interruptora que não precisa ser inserida em sua associação). Feita a ligação, observe o que acontece com o brilho da lâmpada
e responda: em relação ao circuito com apenas uma bateria, o brilho da
lâmpada e a corrente elétrica que circula por ela aumentam ou diminuem
com o acréscimo de uma segunda bateria em série com a primeira?
Nota: lembre-se de inserir um amperímetro no circuito para responder a
essas questões
FIG. 14 - Circuito com duas baterias e uma lâmpada
2) Insira um voltímetro no circuito e utilize-o para medir a voltagem nos
terminais de cada bateria tomada isoladamente, bem como a voltagem
nos terminais da associação formada por duas baterias ligadas em série.
O resultado está dentro do que você esperava? Explique.
3) Volte ao circuito elétrico com uma bateria e uma lâmpada. Depois,
orientando-se pela Figura 15, acrescente uma segunda bateria em paralelo com a primeira. Feita a ligação, responda:
a) Existe diferença significativa no brilho da lâmpada quando ela é
ligada a apenas uma pilha ou a duas pilhas em paralelo?
b) A quantidade de energia que a lâmpada transforma - a cada segundo - é diferente quando ligamos uma pilha ou duas pilhas em paralelo?
E quanto à quantidade de energia entregue por cada pilha?
4) Insira um voltímetro no circuito e utilize-o para medir a voltagem nos
terminais da associação formada por duas baterias ligadas em paralelo.
O número de Joules de energia por Coulomb de carga elétrica é alterado
quando ligamos baterias em paralelo umas com as outras?
FIG. 15 - Baterias em paralelo
Exploração 6.2 - Voltagem em trechos específicos do circuito
As medidas de voltagem podem ser realizadas ao longo de um circuito
que contém dois ou mais elementos associados em série ou em paralelo. Nesse caso, essas medidas deverão estar em acordo com a lei da
conservação da energia. Tal lei, aplicada ao contexto específico dos circuitos elétricos, nos permite compreender os processos de transformação
e transferência de energia nos circuitos. De um lado, temos a fonte de
tensão, que funciona como uma “fonte” de energia e, no caso das baterias, transforma energia potencial química na energia necessária para
deslocar cargas elétricas, de modo a manter uma polaridade ou tensão
entre seus terminais. De outro, temos os aparelhos consumidores, tais
como as lâmpadas, que utilizam a energia fornecida pela fonte de tensão
transformando-a em outras formas de energia como luz e calor. Fixando
2
3
a ideia de que a voltagem em um trecho do circuito mede a energia, em
Joules, que é transferida ou transformada, a cada Coulomb de carga elétrica que atravessa aquele trecho do circuito, faça o que se pede a seguir:
1) Ligue duas lâmpadas em série a uma mesma fonte de tensão. Meça
a voltagem da fonte de tensão e meça, também, a voltagem nos terminais de cada uma das lâmpadas. Considerando que o número de volts
associado à voltagem da fonte nos informa sobre a quantidade de joules
utilizada pela fonte para transportar cada coulomb entre seus terminais,
você diria que as medidas de voltagem, que você acaba de fazer, são
coerentes com a lei da conservação da energia?
2
4
2) Ligue duas lâmpadas em paralelo e meça a voltagem nos terminais
das lâmpadas.
a) Essas medidas coincidem?
b) O número de Coulombs que passa, a cada segundo, no interior
da fonte é igual ao número de Coulombs que passa no interior de cada
lâmpada tomada isoladamente?
c) Você diria que as medidas de voltagem, tanto quanto as considerações sobre a circulação de carga elétrica no circuito em paralelo, são
coerentes com a lei da conservação da energia?
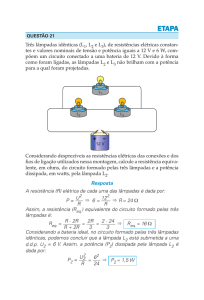
Atividade 7 - Potência elétrica
de um elemento de circuito
Nas atividades 5 e 6 exploramos o significado da medida de voltagem,
construindo a ideia de que essa medida nos informa sobre a quantidade de energia, em Joules, que é transferida ou transformada mediante
a circulação de cargas elétricas, em Coulombs, nos diversos trechos de
um dado circuito. Além da voltagem, há outra medida importante para o
estudo dos circuitos elétricos que também está diretamente associada ao
conceito de energia: a potência elétrica.
A medida da potência elétrica é apenas um caso especial da medida da
grandeza potência. Nos padrões do Sistema Internacional, a potência,
medida em watts, nos informa a quantidade de energia, medida em joules,
que é transferida ou transformada, a cada segundo. Assim, para calcular a potência envolvida em um determinado processo podemos dividir a
quantidade total de energia transferida ou transformada, pelo intervalo de
tempo transcorrido. Em termos da linguagem algébrica essa definição é
expressa como P = ∆E/∆t (equação 1) e a unidade de medida 1 watt =
1 Joule/segundo.
Nos circuitos elétricos, essa definição geral pode ser utilizada para se
deduzir outra expressão, mais específica, que nos permite medir a potência como o produto das grandezas tensão e corrente. Essa nova expressão é P = V . i (equação 2). A transformação da equação 1, mais
geral, na equação 2, mais específica, pode ser compreendida por meio
de uma análise das unidades de medida envolvidas, tal como mostrado
no desenvolvimento apresentado a seguir, em que partimos das unidades
utilizadas na equação 2 para encontrar as unidades de medida utilizadas
na equação 1:
1 Volt x 1 Ampére= 1
Joule x 1 Coulomb = 1 Joule
= 1 Watt
Coulomb
Segundo
Segundo
Procedimentos e questões:
Monte um circuito simples contendo lâmpada, bateria e amperímetro ligados em série. Então, conecte os cabos de um voltímetro nos terminais da
lâmpada, tal como mostrado na Figura 16.
a) Como o brilho da lâmpada é afetado por essas alterações?
b) Se a corrente elétrica (ou seja, a circulação de cargas) é a responsável pela “distribuição” da energia pelo circuito, como podemos explicar
as alterações na quantidade de energia transformada pela lâmpada, uma
vez que o valor da corrente se manteve inalterado?
c) Como a equação P = V . i nos ajuda a compreender essa variação
no brilho da lâmpada?
2) Mantenha a voltagem da bateria em 50 Volts, enquanto altera a resistência da lâmpada, de modo a variar tanto seu brilho, quanto o valor da
corrente que passa em seu filamento.
a) Como o brilho da lâmpada é afetado por alterações no valor da
corrente?
b) Se o valor da voltagem define a quantidade de energia, em joules, que a bateria fornece a cada coulomb de carga que passa em seu
interior, como podemos explicar as alterações na quantidade de energia
transformada pela lâmpada, a partir das mudanças no valor da resistência
de seu filamento?
c) Como a equação P = V . i nos ajuda a compreender a variação no
brilho da lâmpada que ocorre nessas circunstâncias?
FIG. 16 - Amperímetro e voltímetro em um cirtuio em série
Em seguida, clique com o botão direito do mouse sobre a representação
da bateria e acesse a função Alterar Voltagem. Faça o mesmo com a
lâmpada e acesse a função Alterar Resistência. Deixe as duas caixas
com botões deslizantes abertas e situadas em locais que não obstruam a
visão dos elementos do circuito e das representações dedicadas à sinalização do brilho da lâmpada. Feito isso:
1) Observe o brilho da lâmpada enquanto os valores de voltagem e resistência são alterados coordenadamente, de modo a manter constante a
corrente elétrica que passa pelo circuito.
2
5
Atividade 8 - Ligando duas lâmpadas diferentes em um mesmo
circuito
Nesta atividade, investigaremos como a tensão, a corrente e a resistência elétrica determinam a quantidade de energia elétrica transformada,
a cada segundo, em um elemento de circuito. Em outras palavras, investigaremos como tensão, corrente e resistência determinam a potência
elétrica de elementos inseridos em um circuito.
2
6
Procedimentos e questões:
1) Insira duas lâmpadas e uma bateria no lado esquerdo da área de trabalho e mais outras duas com outra bateria no lado direito dessa área.
Em seguida, acesse a função Alterar resistência clicando com o botão
direito do mouse sobre a representação das lâmpadas para aumentar a
resistência elétrica de uma das lâmpadas de cada par elevando seu valor
de 10 ohms (valor original) para 40 ohms.
FIG. 17 - Aumentando a resistência das lâmpadas
2) Utilize o botão direito do mouse para alterar a tensão oferecida por
cada bateria elevando-a dos 9,0 Volts originais para um valor próximo a
24 Volts. Feito isso, monte um circuito com duas lâmpadas em série utilizando as lâmpadas e a bateria que você reuniu à esquerda da área de
trabalho. Com os elementos reunidos à direita, monte outro circuito com
duas lâmpadas em paralelo. Você verá que, nos dois circuitos, uma das
lâmpadas brilhará mais do que a outra. Mas, qual é a lâmpada que, em
cada circuito apresenta um brilho superior: aquela com resistência maior
ou menor?
3) Depois de pensar sobre essa questão e registrar uma justificativa
para sua escolha, clique com o botão direito do mouse na lâmpada que
apresenta o maior brilho em cada circuito e escolha a opção Alterar resistência. Quando essa opção for acionada, o valor atual da resistência
apresentada pela lâmpada de maior brilho irá aparecer. Desse modo, será
possível descobrir se a lâmpada que brilha mais em cada circuito é aquela
que apresenta a maior ou a menor resistência.
4) Caso você tenha falhado em sua previsão, retome seu raciocínio e
seus argumentos e tente compreender como a resistência de duas lâmpadas determina o brilho que as mesmas apresentam quando lidamos
com circuitos em série ou em paralelo. Faça, ainda, medidas de corrente
elétrica e de tensão em diversas partes do circuito, utilizando as funções
voltímetro e amperímetro que podem ser acessadas na área lateral verde
que aparece na interface que se abre com o acionamento da simulação
que estamos a utilizar.
5) Na associação de lâmpadas em série, a corrente que passa pelas duas
lâmpadas é a mesma.
a) Nessa associação, qual das lâmpadas apresentará maior voltagem
(maior queda de potencial): a de maior ou a de menor resistência elétrica?
b) Será que a equação P = V . i nos ajuda a compreender porque a
lâmpada de maior resistência apresenta maior brilho nesse tipo de situação?
6) Na associação de lâmpadas em paralelo, a voltagem aplicada sobre
as duas lâmpadas é a mesma.
a) Nessa associação, qual das lâmpadas será percorrida por maior
corrente elétrica?
b) Será que a equação P = V . i nos ajuda a compreender porque a
lâmpada de menor resistência apresenta maior brilho nesse tipo de situação?
Atividade 9 - Sobrecarregando
uma bateria
Nosso objetivo nesta atividade é simular o comportamento de uma bateria
real sujeita a uma sobrecarga devida ao acréscimo de muitos elementos
consumidores ligados em paralelo no circuito
.
Em algumas casas a ligação do chuveiro produz uma queda no brilho
das lâmpadas, quando várias lâmpadas e outros aparelhos estão ligados
simultaneamente. Algo similar pode ocorrer em um circuito que contém
uma bateria ligada a várias lâmpadas. Nesta atividade iremos investigar
esse processo.
Procedimentos e questões:
1) Conecte uma bateria, uma lâmpada e um amperímetro de modo similar àquele mostrado na Figura 18 (Nota: a configuração mostrada nessa
figura nos ajudará a inserir mais lâmpadas em paralelo nos próximos
passos desta atividade). Observe o brilho da lâmpada e a corrente que
circula em seu filamento para futuras comparações. Depois disso, clique
no o botão direito do mouse sobre a representação da bateria e escolha
a função Alterar Resistência Interna. Na caixa de diálogo que se abrirá,
aumente a resistência interna da bateria de zero para 5 ohms. Observe,
então, o que acontece com o brilho da lâmpada e com a corrente elétrica
que circula no circuito.
FIG. 18 - Lâmpada e
amperímetro
2
7
2) Acrescente mais lâmpadas ao circuito, sempre ligadas em paralelo
umas com as outras (Figura 19). Fixe sua atenção no brilho da primeira
lâmpada, enquanto novas lâmpadas são acrescentadas. Se tiver dificuldade em fazê-lo experimente o processo inverso e desconecte progressivamente um dos terminais de cada lâmpada inserida, tal como mostrado
na figura ao lado. Enquanto desconecte as lâmpadas, observe com aten-ção possíveis alterações no brilho da primeira lâmpada, bem como o valor da corrente total do circuito (corrente que atravessa a bateria). Como
parecem estar relacionados: o número de lâmpadas ligadas em paralelo,
e a corrente total do circuito e o brilho da primeira lâmpada?
3) Conceba uma hipótese para explicar o fato de que o aumento no número de lâmpadas ligadas em paralelo a uma única bateria acaba por
produzir uma queda no brilho que cada uma delas apresenta. Experimente
fazer medidas com o multímetro para avaliar qualquer uma de suas hipóteses ou explicações.
4) Nas atividades 1 e 2, nós caracterizamos a ligação em paralelo como
aquela na qual o ato de ligar ou desligar uma lâmpada ao circuito não
afetava a conexão entre a(s) outra(s) lâmpada(s) e a fonte de tensão. A
partir do que observamos agora, você diria que esta ainda é uma maneira
geral de caracterizar a ligação de lâmpadas em paralelo. Justifique!
5) Se você ainda não o fez, experimente medir a tensão ou voltagem nos
terminais da bateria enquanto acrescenta mais e mais lâmpadas em paralelo ao circuito. A partir destas medidas, responda: que efeito o aumento
do número de lâmpadas em paralelo produz sobre a tensão oferecida pela
bateria?
2
8
6) Para manter a tensão em seus terminais, uma bateria precisa exercer
uma espécie de “força eletromotriz” transferindo cargas elétricas entre
seus terminais positivo e negativo. A queda de tensão nos terminais da
fonte verificada no item anterior está de algum modo associada a uma
possível mudança na corrente elétrica total estabelecida no interior da
fonte? Explique.
FIG. 19 - Lâmpadas em paralelo
Atividade 10 - Previsões e desafios em circuitos mistos
Nesta atividade utilizaremos os conceitos de diferença de potencial, resistência elétrica, corrente e potência elétrica em circuitos mais complexos.
As situações exploradas exigem e estimulam uma compreensão mais
integrada desses conceitos.
Antes de usar a simulação para responder a cada questão apresentada
a seguir, analise atentamente os diagramas que representam os circuitos
e faça as previsões solicitadas. Só depois de ter feito e registrado, por
escrito, suas previsões é que você deve usar a simulação para montar os
circuitos e observar seu comportamento. Caso ocorra alguma divergência
entre previsões e observações, procure identificar o que você deixou de
levar em consideração e conceber novas explicações para o comportamento exibido pelos circuitos observados.
Exploração 10.1 - Lâmpada em série com associação de lâmpadas em
paralelo
Os desafios 1, 2, 3 e 4 envolvem previsões sobre características do
circuito da Figura 20. Esse circuito contém uma lâmpada A ligada em
série com uma associação em paralelo formada pelas lâmpadas B e C. A
diferença de potencial entre os pontos 1 e 2 é estabelecida por duas baterias ligadas em série e mantém-se constante, mesmo quando o circuito
é alterado. As três lâmpadas apresentam resistências idênticas quando
estão inseridas nesse circuito. Os fios condutores são considerados ideais
(têm resistência elétrica desprezível).
FIG. 20 - Circuito com lâmpadas em série e paralelo
1) Faça uma previsão quanto ao brilho das três lâmpadas (A, B e C)
colocando-as em ordem crescente de brilho ou, indicando, quando for o
caso, quais têm mesmo brilho. Depois disso, e antes de montar o circuito
no simulador:
a) Suponha que a lâmpada C seja desconectada do circuito e, nesse
caso, diga se os brilhos de A e B mudarão. Em caso positivo, diga como.
b) Com a remoção da lâmpada C, o que aconteceria com a corrente
no ponto 3? Explique o seu raciocínio.
c) Depois de fazer suas previsões para os itens (a) & (b), e de registrar o seu raciocínio por escrito, monte o circuito, desconecte a lâmpada
C e compare previsões e observações.
2
9
2) Volte a montar o circuito mostrado na figura 10.1. Faça as três previsões solicitadas a seguir para só depois produzir as alterações no circuito
que serão indicadas. Por fim, compare suas previsões e observações.
a) O que aconteceria com o brilho de cada lâmpada caso um fio fosse
ligado entre os pontos 3 e 4?
b) O que aconteceria com a diferença de potencial entre os pontos 4
e 5 nessa nova configuração do circuito?
c) O que aconteceria com a corrente no ponto 5 em virtude da ligação
criada entre os pontos 3 e 4?
3
0
3) Volte a montar o circuito mostrado na figura 10.1. Faça as três previsões solicitadas a seguir para só depois produzir as alterações no circuito
que são indicadas nas solicitações. Por fim, compare suas previsões e
observações.
a) O que aconteceria com o brilho de cada lâmpada caso um fio fosse
ligado entre os pontos 4 e 5 do circuito?
b) O que aconteceria com a corrente no ponto 2 nessa nova configuração do circuito?
c) O que aconteceria com a diferença de potencial entre os pontos 2
e 4 em virtude da inserção de um fio condutor conectado entre os pontos
4 e 5 do circuito?
Exploração 10.2 - Lâmpada em paralelo com associação de lâmpadas
em série
Os desafios 1 e 2 propostos a seguir envolvem previsões sobre características e alterações no circuito da Figura 21. Esse circuito contém uma
lâmpada A associada em paralelo com um trecho de circuito que apresenta duas lâmpadas B e C ligadas em série. A diferença de potencial
entre os pontos 1 e 2 é estabelecida por duas baterias ligadas em série
e mantém-se constante, mesmo quando o circuito é alterado. As três
lâmpadas apresentam resistências idênticas quando estão inseridas nesse circuito. Os fios condutores são considerados ideais (têm resistência
elétrica desprezível).
FIG. 21 - Circuito de lâmpadas em paralelo e se série
1) Antes de montar o circuito da figura 10.2, compare o brilho das três
lâmpadas (A, B e C) colocando-as em ordem crescente de brilho. Depois
disso, e antes de montar o circuito no simulador:
a) Suponha que a lâmpada A seja removida do seu soquete e, nesse
caso, diga se os brilhos de B e C mudarão. Em caso positivo, diga como.
b) Com a remoção da lâmpada A, o que aconteceria com a corrente
nos pontos 3, 4 e 5? Explique o seu raciocínio.
c) Suponha que a lâmpada A seja mantida, mas que a lâmpada C seja
removida do seu soquete e, nesse caso, diga se os brilhos de A e B mudarão. Em caso positivo, diga como.
d) Com a remoção da lâmpada C, o que aconteceria com a corrente
nos pontos 3, 4 e 5? Explique o seu raciocínio.
2) Volte a montar o circuito mostrado na figura 10.2. Faça as três previsões solicitadas a seguir para só depois produzir as alterações no circuito
que serão indicadas. Por fim, compare suas previsões e observações.
a) O que aconteceria com o brilho de cada lâmpada, caso um fio fosse
ligado entre os pontos 1 e 4 do circuito?
b) O que aconteceria, simultaneamente, com a corrente no ponto 3?
c) O que aconteceria com a diferença de potencial entre os terminais
das lâmpadas B e C?
Exploração 10.3 - Circuito em paralelo formado por dois conjuntos de
lâmpadas em série
A Figura 22 mostra um circuito com lâmpadas idênticas. Note que um
trecho do circuito contém duas lâmpadas A e B ligadas em série uma
com a outra. Paralelamente a esse primeiro trecho, há outro trecho que
contém duas lâmpadas C e D também associadas em série uma com a
outra. A diferença de potencial entre os pontos 1 e 2 é estabelecida por
duas baterias ligadas em série e mantém-se constante, mesmo quando
o circuito é alterado.
1) Analisando esse circuito, preveja o que aconteceria:
a) No interior de um fio usado para conectar os pontos 3 e 4 do circuito.
b) Com o brilho das lâmpadas, após a inserção do fio mencionado no
item (a).
c) Com a corrente elétrica que circula nos pontos 1 e 2, após a inserção do fio mencionado no item (a).
d) Com a diferença de potencial em cada lâmpada, após a inserção do
fio mencionado no item (a).
2) Depois de fazer suas previsões para os itens (a), (b), (c) e (d) e após
registrar o seu raciocínio, por escrito, monte o circuito, conecte os pontos
3 e 4 por meio de um fio de ligação e compare previsões e observações.
3
1
FIG. 22 - Circuito de lâmpadas em paralelo e se série