Universidade Federal do ABC Rua Santa Adélia, 166

Universidade Federal do ABC
Rua Santa Adélia, 166 - Bairro Bangu Santo André - SP - Brasil
CEP 09.210-170 - Telefone/Fax: +55 11
4996-3166
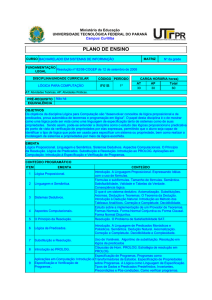
1. CÓDIGO E NOME DA DISCIPLINA
BC1426 - LÓGICA BÁSICA
2.
DISCIPLINA
(RECOMENDAÇÃO)
REQUISITO 3. INDICAÇÃO DE CONJUNTO (BCC)
Obrigatória
4. CURSO
BACHARELADO EM CIÊNCIA DA
COMPUTAÇÃO
6. QUADRIMESTRE IDEAL
6
5. CRÉDITOS
T P I: 4-0-4
7. NÍVEL
Graduação
8. Nº. MÁXIMO DE ALUNOS POR TURMA
TEORIA: 60
LABORATÓRIO: 30
9. OBJETIVOS
–
Apresentar conceitos e teoremas de lógica de primeira ordem clássica, seus
e usos.
–
Apresentar diferentes métodos de prova para lógica proposicional, de forma
que o aluno possa trabalhar com cálculo proposicional.
–
Apresentar conceitos e elementos da lógica de primeira ordem
–
Apresentar conceitos e elementos básicos da linguagem Prolog.
–
Apresentar o Paradigma de programação em Logica
10. COMPETÊNCIAS
A disciplina deverá permitir o aluno ser capaz de:
-Compreender os fundamentos da lógica proposicional clássica e da lógica de predicados;
-Compreender diferentes métodos de validação de teoremas e programas.
-Fazer uso do cálculo proposicional de métodos de prova
-Desenvolver sistemas baseados no paradigma de programação em lógica.
11. PROGRAMA RESUMIDO (EMENTA)
Conceitos básicos e elementos de lógica proposicional, regras de inferência,
“fórmulas bem formadas”, métodos de prova, lógica de predicados de primeira
ordem, sintaxe e semântica de Prolog e Sistemas Especialista.
12. PROGRAMA
1. Lógica e Cálculo Proposicional
1.1. Aspectos históricos de lógica
1.2. Conceitos básicos: proposição, teorema, Tautologia, Contradição
Universidade Federal do ABC
Rua Santa Adélia, 166 - Bairro Bangu Santo André - SP - Brasil
CEP 09.210-170 - Telefone/Fax: +55 11
4996-3166
1.3. Manipulação tabela verdade
1.4. Lógica proposicional: semântica e sintaxe
1.5. wwwf's
1.6. Métodos de prova: direta, por contradição e por resolução
1.7. Simplificação de wwf's
2. Cálculo de predicados de primeira ordem
2.1. Linguagem de primeira ordem (variável, quantificador, predicado, fórmula)
2.2. Igualdade
2.3. Definição recursiva e indução finita
2.4. Dedução, conseqüência sintática e teorema
2.5. Noção de sistema axiomático
3. Programação em lógica
3.1. Paradigma de programação em lógica
3.2. Sintaxe e Semântica do Prolog
3.3. Recursos do Prolog
3.4. Backtracking
3.5. Sistemas especialistas
13. MÉTODOS UTILIZADOS
A teoria e os métodos da disciplina são apresentados através de aulas expositivas,
intercaladas com aulas de exercícios e com aulas práticas no laboratório de
informática.
14. ATIVIDADES DISCENTES
Aulas teóricas expositivas, exercícios e trabalhos extra-classe (em grupo ou
individual), aulas pr'ticas no labratório, pesquisa bibliográfica, seminários e debates,
atividades de avaliação propostas.
15. CARGA HORÁRIA
AULAS TEÓRICAS: 24hs
AULAS PRÁTICAS: 24hs
TOTAL: 48hs
RECOMENDADO PARA DEDICAÇÃO INDIVIDUAL:
04hs/semana
16. CRITÉRIOS DE AVALIAÇÃO DE APRENDIZAGEM
O conceito será composto da seguinte forma: 70% do aproveitamento correspondendo
às provas escritas e 30% correspondendo às demais atividades (lista de exercícios,
exercícios-programas e projeto de sistema especialista).
17. NORMAS DE RECUPERAÇÃO (CRITÉRIOS DE APROVAÇÃO E ÉPOCAS DE
REALIZAÇÃO DAS PROVAS OU TRABALHOS)
As notas serão atribuídas segundo os conceitos estabelecidos pela UFABC. A
Universidade Federal do ABC
Rua Santa Adélia, 166 - Bairro Bangu Santo André - SP - Brasil
CEP 09.210-170 - Telefone/Fax: +55 11
4996-3166
aprovação se dará mediante obtenção de conceitos A, B, C, ou D. Será aplicado uma
prova substitutiva no final do trimestre como possibilidade de recuperação na
disciplina.
18. BIBLIOGRAFIA RECOMENDADA
BIBLIOGRAFIA BÁSICA:
1.
SCHINERMAN, E. Matemática Discreta: uma introdução, 2 ed., São
Paulo: Cenage leraning, 2011. 573 p
2. GERSTIG J.L., Fundamentos matemáticos para Ciência da Computação : Um
Tratamento de Matemática Discreta, LTC, 5a edição, 2004.
3. MORTARI, C. Introdução à Lógica, Editora Unesp, 2001.
BIBLIOGRAFIA COMPLEMENTAR:
1.
BITTENCOURT, G. Inteligência Artificial: Ferramentas e teorias, UFSC,
3a. Edição, 2006
2.
RUSSEL, S., NORVIG, P., Artificial Intelligence: A modern Approach,
2nd ed Prentice Hall, 2003.
3.
FITTING M., MENDELSOHN, R. L., First-Order Modal Logic, Klumer,
1998.
4.
CARNIELLI, W. & EPSTEIN, R. L. Computabilidade: funções
computáveis, lógica e os fundamentos da matemática. São Paulo, Unesp /
Fapesp, 2006.
5.
COSTA, N. A., Ensaio sobre os Fundamentos da Lógica, São Paulo,
Hucitec, 1980.
Aula 01: Apresentação da disciplina.
Aula 02: Introdução e Conceitos básicos.
Aula 03: Manipulação de tabelas verdades
Aula 04: Prova usando Tabela Verdade
Aula 05: Lógica proposicional: semântica e sintaxe
Aula 6: “Fórmula bem formadas”
Aula 7: Regras de Inferência
Aula 8: Prova direta
Aula 9 : Prova direta
Aula 10: Resolução de Exrecícios
Aula 11: Prova por contradição
Aula 12: Prova por resolução
Aula 13: Prova por resolução/ Simplificações de wwf's
Aula 14: Primeira Avaliação teórica
Aula 15: Linguagem de primeira ordem
Aula 16: Igualdade, definição recursiva e indução finita
Universidade Federal do ABC
Rua Santa Adélia, 166 - Bairro Bangu Santo André - SP - Brasil
CEP 09.210-170 - Telefone/Fax: +55 11
4996-3166
Aula 17: Dedução, conseqüência sintática, teorema e noção de sistema axiomático
Aula 18: Paradigma de programação em lógica
Aula 19: Sintaxe e Semântica do Prolog
Aula 20: Recursos do Prolog
Aula 21: Backtracking
Aula 22: Sistemas especialistas
Aula 23: Segunda Avaliação Teórica
Aula 24: Apresentação do projeto em Prolog
20. PROFESSOR(A) RESPONSÁVEL
Luis Paulo Scott