Tensões em reservatórios de parede fina – acetatos da aula

INSTITUTO POLITÉCNICO DE BRAGANÇA – Engenharia Civil
Mecânica Aplicada 2 – Teoria do Estado de Tensão
Tensões em reservatórios de parede fina
Pode assumir-se que as forças internas exercidas sobre um elemento da parede são
tangentes à superfície do reservatório.
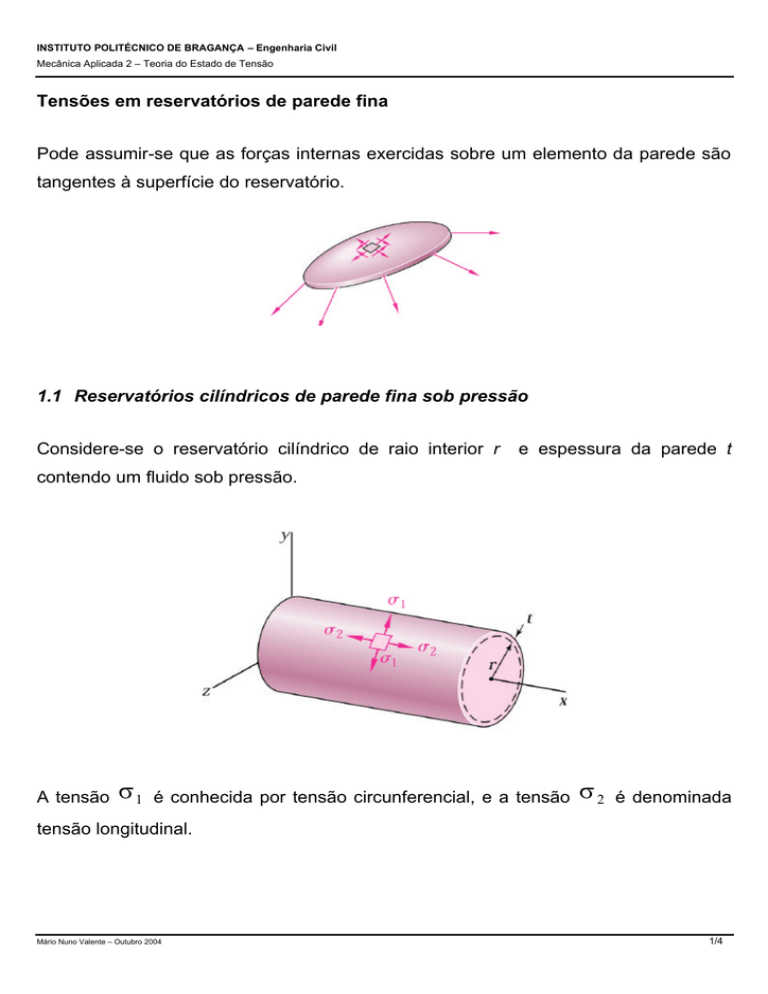
1.1 Reservatórios cilíndricos de parede fina sob pressão
Considere-se o reservatório cilíndrico de raio interior r
e espessura da parede t
contendo um fluido sob pressão.
A tensão
σ1
é conhecida por tensão circunferencial, e a tensão
σ2
é denominada
tensão longitudinal.
Mário Nuno Valente – Outubro 2004
1/4
INSTITUTO POLITÉCNICO DE BRAGANÇA – Engenharia Civil
Mecânica Aplicada 2 – Teoria do Estado de Tensão
∑F
=0
∑F
=0
z
x
Mário Nuno Valente – Outubro 2004
2/4
INSTITUTO POLITÉCNICO DE BRAGANÇA – Engenharia Civil
Mecânica Aplicada 2 – Teoria do Estado de Tensão
1.2 Reservatórios esféricos de parede fina sob pressão
Considere-se agora um reservatório esférico de parede
fina de raio interior r e parede de espessura t, contendo
um fluido submetido a uma diferença de pressão
interna p. Por razões de simetria, as tensões exercidas
sobre as quatro faces de um pequeno elemento de
parede têm de ser iguais.
σ1 = σ 2
Mário Nuno Valente – Outubro 2004
3/4
INSTITUTO POLITÉCNICO DE BRAGANÇA – Engenharia Civil
Mecânica Aplicada 2 – Teoria do Estado de Tensão
Exercício
Uma conduta de aço tem 900 mm de
diâmetro exterior e liga a albufeira em A à
turbina hidráulica em B. Sabendo que o peso
específico da água é 9800 N/m3, determine a
tensão normal máxima e a tensão tangencial
máxima na conduta em condições estáticas.
Exercício
O tanque de ar comprimido indicado é fabricado a
partir de uma chapa de 6 mm de espessura e
soldada ao longo de uma hélice que forma um
ângulo β = 30º com a horizontal. Sabendo que a
tensão normal admissível no cordão de soldadura
é 75 MPa, determine a máxima pressão interna a
que o tanque pode ser submetido.
Mário Nuno Valente – Outubro 2004
4/4