5- Método de Elementos Finitos Aplicado às Equações Diferenciais

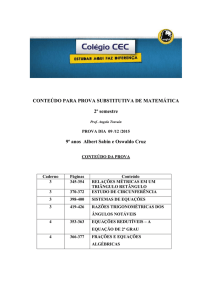
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS
5- Método de Elementos Finitos
Aplicado às Equações
Diferenciais Parciais.
5.1- Breve Introdução Histórica.
5.2- Solução de Equações Diferenciais
Ordinárias: Problema de Valor de Contorno.
5.3- Solução de Equações Diferenciais
Parciais: Problema de Valor de Contorno.
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Apresentaremos o MEF para um Problema de Valor de Contorno
em Duas Dimensões. Especificamente, para a Equação
Bidimensional da Difusão-Adveção-Reação Linear e Estacionaria
definida num domínio quadrado unitário com condições de
contorno de Dirichlet. Chamaremos este Problema de Valor de
Contorno (PVC) de Problema Modelo.
Tradicionalmente o PVC é descrito na Formulação Forte.
Formulação Forte (PVC): Encontrar u ∈ S Forte tal que satisfaz
r
∇ ⋅ (− k ∇u ) + ω
⋅ ∇u + σ
u = {
g (x)
∀ x ∈ Ω (EDP)
{
14243 {
Advecção
Reação
Difusão
u (Γ ) = uΓ
Fonte Externa
{Condição de Dirichlet
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Para obter a Formulação Fraca partindo da Formulação Forte do
PVC devemos realizar os cinco passos a seguir:
∞
Passo 1. Multiplicar a EDP por uma função “Teste” v ∈ C0 (Ω ) .
∞
C
O símbolo 0 (Ω ) denota o espaço das funções continuas com
derivadas até ordem ∞ continuas em Ω e que se anulam no
contorno Γ.
r
[∇ ⋅ ( − k ∇ u ) + ω ⋅ ∇ u + σ u ] v = g ( x ) v
∀ x ∈ Ω (EDP)
Passo 2. Integrar sobre o domínio Ω .
r
∫ [∇ ⋅ ( − k ∇ u ) + ω ⋅ ∇ u + σ u ] vd Ω = ∫ g ( x ) v d Ω
Ω
Ω
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Passo 3. Use Integração por Partes (ou use a formula de Green ou
teorema de Gauss) para reduzir a derivada de maior ordem da
b
EDP. b
b
∫ udv = uv
a
− ∫ vdu (Integração por Partes)
a
a
∂u
∂v
vd
Ω
=
−
u
∫Ω ∂xi
∫Ω ∂xi d Ω + ∫Γ uvni d Γ (Teorema de Gauss)
r
n = ( n1 , n2 ,L , nd ) vetor unitário normal ao contorno Γ no sentido da saida de Γ.
r
∫ [ k (∇u ⋅ ∇v) + (ω ⋅ ∇u )v + σ uv ] d Ω − ∫ uvn d Γ = ∫ g (x)v(x)d Ω
i
Ω
Γ
Ω
Passo 4. Como v ∈ C0∞ (Ω ) , v se anula no contorno Γ obtemos
r
∫ [ k (∇u ⋅ ∇v) + (ω ⋅ ∇u )v + σ uv ] d Ω = ∫ g (x)v(x)d Ω
Ω
Ω
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Passo 5. Encontrar o maior espaço de funções para u, v e as
outras funções que aparecem no Passo 4 tal que todas as integrais
sejam finitas.
Se u ∈ C (Ω) ∩ C (Ω) ≡ S Forte (restrições de regularidade para a
Formulação Forte do PVC) e v ∈ C0∞ (Ω ) , então todas as integrais
serão finitas. Entretanto, todas as integrais serão finitas também se
2
{
}
{
u ∈ S = φ ∈ H 1 (Ω) : φ = u (Γ) em Γ e v ∈ V = φ ∈ H 1 (Ω) : φ = 0 em Γ
}
Onde os seguintes espaços de funções são definidos:


L ( Ω ) = φ : (φ , φ ) ≡ ∫ φφ d Ω < ∞  (Espaço das funções quadrado integravei s)

Ω

dφ


H 1 (Ω) = φ ∈ L2 (Ω) e
∈ L2 (Ω) e H 01 (Ω) = φ ∈ H 1 (Ω) : φ = 0 em Γ
dx


2
{
}
Com isto podemos enunciar a Formulação Fraca correspondente à
Formulação Forte do PVC como segue:
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Formulação Fraca (Variacional): Encontrar u ∈ S que satisfaz
r
∫ [ k (∇u ⋅ ∇v) + (ω ⋅ ∇u )v + σ uv ] d Ω = ∫ g (x)v(x)d Ω
Ω
144444424444443
A ( u ,v )
∀v ∈ V
Ω
144244
3
F (v)
ou na forma compacta A(u, v) = F (v)
∀v ∈ V
Equivalência entre a Formulação Fraca e Forte:
1- A solução da Formulação Forte é também solução da
Formulação Fraca.
2- Quando a solução da Formulação Fraca é suficientemente
2
regular u ∈ C (Ω) ∩ C (Ω) ≡ S Forte também será solução da
Formulação Forte.
Formulação Forte
Formulação Fraca
ou
Equação Diferencial Parcial
Equação Variacional
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Método de Elementos Finitos: Seja M h =ne{Ω1,K, Ωne} uma partição de Ω
em ne elementos da malha tal que Ω = e∪=1 Ωe e Ωe ∩ Ωe' = 0 se e ≠ e'
(elementos disjuntos). O diâmetro (parâmetro) da malha é definido
{he } , onde he é o diâmetro de cada elemento finito.
como h = 1max
≤ e ≤ ne
r
k
(
∇
u
⋅
∇
v
)
+
(
ω
⋅ ∇u )v + σ uv ] d Ω = ∫ g ( x)v ( x ) d Ω
∫Ω [
144444424444443 Ω144244
3
A ( u ,v )
ne
A( u , v ) = ∑
F (v)
ne
r
e
k
(
∇
u
⋅
∇
v
)
+
(
ω
⋅
∇
u
)
v
+
σ
uv
d
Ω
=
A
[
]
∑ (u , v )
∫
e =1 Ω e
144444424444443
e =1
Ae ( u , v )
ne
F (v ) = ∑
∫
e =1 Ω e
ne
g ( x )v ( x ) d Ω = ∑ F e (v )
144244
3
e =1
F e (v)
ne
ne
A(u , v ) = F (v ) ⇔ ∑ A (u , v ) = ∑ F e (v )
e
e =1
e =1
Note que até aqui
não tem nenhuma
aproximação
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
O Método de Elementos Finitos de Galerkin é baseado na escolha
de uma base local para o espaço V h ⊂ V. Ou seja, uma base para
cada elemento da malha. Na maioria das vezes para construir esta
k
base são usados os polinômios P (Ωe ). Construiremos a base para
elementos quadriláteros usando polinômios lineares k=1. Existem
outros elementos como os triangulares.
e
As funções “forma” ηl ( x, y ) da base podem ser
os polinômios de Lagrange:
( x − x2e )( y − y 4e )
η ( x, y ) = e
( x1 − x2e )( y1e − y 4e )
e
1
( x − x1e )( y − y 3e )
η ( x, y ) = e
( x2 − x1e )( y 2e − y 3e )
e
2
( x − x1e )( y − y 2e )
η ( x, y ) = e
( x2 − x1e )( y 3e − y 2e )
e
3
A solução restrita ao elemento
4
u e ( x, y ) = ∑ uieηie ( x, y ) ∀( x, y ) ∈ Ω e
i =1
( x − x2e )( y − y1e )
η ( x, y ) = e
( x1 − x2e )( y 4e − y1e )
e
4
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Note que as funções “forma” ηle ( x, y ) da base verificam ηl ( xm , ym ) = δ lm
e
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Substituindo para calcular a matriz de cada elemento e o termo
independente segue:
r
∫ [ k (∇u ⋅ ∇v) + (ω ⋅ ∇u )v + σ uv ] d Ω
A e (u , v ) =
Ωe
F e (v ) =
∫ g ( x )v ( x ) d Ω
Ωe
4
u ( x, y ) = ∑ uieηie ( x, y ) ∀( x, y ) ∈ Ω e
e
i =1
4
A (u ,η ) = ∑ u ej
e
e
e
i
j =1
r
e
e
e
e
e e


k
(
∇
η
⋅
∇
η
)
+
(
ω
⋅
∇
η
)
η
+
ση
j
i
j
i
jη i  d Ω
∫Ω 
e
14444444
4244444444
3
aije
F (η ie ) =
∫
g ( x, y )η ie d Ω
Ωe
144244
3
f ie
Desta forma calculamos a contribuição de cada elemento e
incorporamos na matriz e o vetor independente global.
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Para o caso de uma malha uniforme com todos os elementos
iguais podemos fazer estes cálculos de forma analítica. Isto é
possível porque a matriz para cada elemento e o vetor do termo
independente serão “iguais” para todos os elementos. Apenas é
necessário calcular um.
Mas se a malha não é
deste tipo os cálculo
analíticos são muito
trabalhosos. Neste caso
é necessário realizar
uma transformação
(mapeamento
isoparamétrico) para que
todos os elementos
sejam transformados em
um único elemento
(elemento padrão).
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
As funções bases para o elemento padrão bilinear Ωˆ e são ηle (ξ1, ξ2 ):
1
(ξ 1 − 1)(ξ 2 − 1)
4
1
η 2e (ξ1 , ξ 2 ) = − (ξ1 + 1)(ξ 2 − 1)
4
1
η 3e (ξ1 , ξ 2 ) = (ξ1 + 1)(ξ 2 + 1)
4
1
η 4e (ξ1 , ξ 2 ) = − (ξ1 − 1)(ξ 2 + 1)
4
η 1e (ξ1 , ξ 2 ) =
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Com esta mudança de variáveis temos x(ξ1, ξ2 ) e y (ξ1, ξ2 ) :
ˆ 
∀x ∈ Ωe x(ξ1 , ξ 2 ) = ∑ xieηi (ξ1, ξ 2 ) ∀(ξ1 , ξ 2 ) ∈ Ω
e 

i =1

4
ˆ 
∀y ∈ Ωe y (ξ1, ξ 2 ) = ∑ yieηi (ξ1 , ξ 2 ) ∀(ξ1 , ξ 2 ) ∈ Ω
e

i =1
4
ˆ → Ω
T :Ω
e
e
−1
ˆ → Ω
T :Ω
e
e
A matriz Jacobiana desta transformação e sua inversa são:
 ∂x
 ∂ξ
1
J=
 ∂y
 ∂ξ
 1
∂x 
∂ξ 2 
 e
∂y 
∂ξ 2 
 ∂y
 ∂ξ
1
 2
J −1 =
det J  ∂y
 − ∂ξ
1

∂x 
∂ξ2 
1 0
 , onde JJ −1 = 

∂x 
0
1


∂ξ1 
−
Um elemento padrão é chamado de isoparamétrico se as funções
forma (base) podem ser usadas para representar tanto o
mapeamento de Ωˆ e em Ωe quanto da função de interpolação
4
ˆ
u (ξ1, ξ 2 ) = ∑ uieηie (ξ1 , ξ 2 ) ∀(ξ1, ξ 2 ) ∈ Ω
e
e
i =1
ˆ ) → u (Ω )
u (Ω
e
e
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Existem restrições para garantir a existência da transformação
ˆ → Ω . Isto implica em restrições para malhas
inversa T − 1 : Ω
e
e
com elementos muito distorcido. Para garantir a existência da
transformação inversa é necessário exigir para todos os elementos
e
e
da malha que det J ( xi , yi ) > 0 ∀i = 1,L , 4 . Ou seja, devem ser evitadas
malhas com elementos deste tipo.
Lembrando que estamos querendo calcular para cada elemento e
com a mudança de variáveis segue:
r
e
e
e
e

a (η j ,η i ) = ∫  k (∇η j ⋅ ∇η i ) + (ω ⋅ ∇η ej )η ie + ση ejη ie  d Ω =
Ωe
144444444244444444
3
aije
∫
r
 k (∇η ej ⋅ ∇ηie ) + (ω ⋅ ∇η ej )ηie + ση ejη ie  det J d ξ1d ξ 2
ˆ
Ω
e
f (η ie ) =
∫
g ( x, y )η ie d Ω =
Ωe
144244
3
f ie
∫
ˆ
Ω
e
g (ξ1 , ξ 2 )η ie det J d ξ1d ξ 2
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Devemos agora determinar as derivadas das funções base com
respeito as novas coordenadas do elemento padrão.
e
e
e
e
e
e




∂
η
∂
η
∂
η
∂
η
∂
η
∂
η
ξ
ξ
∂
∂
∂
ξ
j
j
j
j
j
j ∂ξ 2
e
1
2
1
∇η j = 
,
=
+
,
+
 ∂x ∂y   ∂ξ ∂x ∂ξ ∂x ∂ξ ∂y ∂ξ ∂y 
2
1
2

  1

 ∂η ej

=  ∂ξ1
 ∂ξ
∂η ej   1
  ∂x
∂ξ 2 
 ∂ξ 2
 ∂x

∂ξ1 
∂y 

∂ξ 2 
∂y 
A matriz coincide com a matriz inversa da matriz Jacobiana:
 ∂ξ1
 ∂x

 ∂ξ 2
 ∂x

∂ξ1 
 ∂y
 ∂ξ
∂y 
1
 2
 = J −1 =
∂ξ 2 
det J  ∂y
−


∂y 
 ∂ξ1
∂x 
∂ξ 2 

∂x 
∂ξ1 
−
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
Agora estamos em condições de calcular:
a (η ,η ) =
e
j
e
i
∫
r
 k (∇η ej ⋅ ∇η ie ) + (ω ⋅ ∇η ej )η ie + ση ejη ie  det J d ξ1d ξ 2
ˆ
Ω
e
1 1
=
∫
r
e
e
e
e
e e


k
(
∇
η
⋅
∇
η
)
+
(
ω
⋅
∇
η
)
η
+
ση
j
i
j
i
jη i  det J d ξ1d ξ 2
∫
− 1 −1
f (η ie ) =
∫
g (ξ1 , ξ 2 )η ie det J d ξ1d ξ 2 =
1 1
∫
e
g
(
ξ
,
ξ
)
η
∫ 1 2 i det J d ξ1d ξ2
−1 − 1
ˆ
Ω
e
Como as funções integrando são polinômios estas integrais podem
ser calculadas de forma exata usando quadratura de Gauss com
um número de pontos de Gauss adequado para o grau dos
polinômios usados.
1 1
∫
npg npg
m
n
e
m
n
m
n
g
(
ξ
,
ξ
)
η
det
J
d
ξ
d
ξ
≈
w
w
g
(
ξ
,
ξ
)
η
(
ξ
,
ξ
)
det
J
(
ξ
,
ξ
∑∑ m n 1 2 i 1 2
1
2
1
2)
∫ 1 2
−1 − 1
e
i
m =1 n =1
5.3- Solução de Equações Diferenciais Parciais:
Problema de Valor de Contorno.
e
Se a função integrando g (ξ1 , ξ 2 )ηi (ξ1 , ξ 2 ) é um polinômio de grau N
e usamos npg pontos de Gauss na quadratura, então a quadratura
de Gauss será exata se N ≤ 2 npg − 1. Finalmente, todas estes
procedimentos para calcular a matriz do elemento e o vetor
independente podem ser implementados em algoritmo
computacional.
De posse das matrizes e vetores dos elementos é montada a
matriz global e o vetor independente global.
Isto resulta num sistema de equações algébricas lineares KU = F
que pode ser resolvido por algum método já estudado.
Existem outros tipos de elementos padrões que podem ser
encontrados na bibliografia. Entretanto o procedimento para chegar
no sistema de equações algébrico linear é o mesmo ao
apresentado nesta aula.
Frase do Dia
Perguntaram ao Dalai Lama …
O que mais te surpreende na Humanidade?
“Os homens… Porque perdem a saúde para juntar
dinheiro, depois perdem dinheiro para recuperar a
saúde.
E por pensarem ansiosamente no futuro, esquecem
do presente de tal forma que acabam por não
viver nem o presente nem o futuro.
E vivem como se nunca fossem morrer...
...e morrem como se nunca tivessem vivido.