Astronomia também para astrólogos

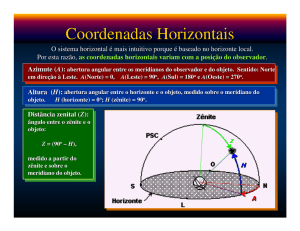
Astronomia
... também para astrólogos
Prof. Luiz Ferraz Netto [Léo]
[email protected]
[email protected]
Céu e Terra - noções básicas
#1 - Resumo histórico
A cada dia o universo todo (esfera celeste) parece efetuar uma revolução completa em torno do
observador, suposto fixo, na superfície da Terra. Este movimento é só aparente e deve-se ao
movimento real de rotação da Terra em torno do seu eixo diametral Sul-Norte (do qual o
observador não tem noção direta).
A Terra circunda o Sol, tal como os demais planetas, em movimento de translação elíptica. A Lua
é satélite da Terra.
Inventada na Holanda (1608), a luneta astronômica foi modificada por Galileu (1609- ocular
divergente). Com sua luneta, Galileu descobriu os satélites de Júpiter, o que contribuiu para
prestigiar o Sistema Planetário concebido por Copérnico. Baseando-se nas medições
astronômicas realizadas por Tycho Brahe, Kepler enunciou as três leis que descrevem o
movimento dos planetas (cinemática). Com bases nestas, Newton descobriu a Lei da Gravitação
Universal, assim estendendo ao Cosmos as Leis da Dinâmica descobertas na Terra.
#2 - Ptolomeu e Copérnico – Referenciais
Astronomia significa leis dos movimentos dos astros. O estudo de qualquer movimento requer a
adoção de um referencial, isto é, um corpo geométrico rígido adequado para determinar
inequivocamente a posição do móvel em qualquer data. Pode ser um sistema de três eixos Ox,
Oy e Oz perpendiculares dois a dois (referencial cartesiano). Em geografia adota-se sistema de
referência constituído por planos paralelos e planos meridianos; as correspondentes coordenadas
são a latitude  e a longitude  (figura 01); segundo a vertical do lugar mede-se a altitude.
1
Figura 01 - Ponto genérico P no espaço é
determinado univocamente por suas
coordenadas no referencial adotado. Na
figura representam-se dois referenciais:
c1- Referencial cartesiano Oxyz com
origem O, eixo das abscissas Ox, eixo de
ordenadas Oy, eixo de cotas Oz, normais
entre
si
dois
a
dois.
e1- Referencial esférico Or com origem
no centro O, distância P à origem |OP| = r,
eixo Oz, plano-base z=0 (o próprio plano
xOy), plano-meridiano-de-orígem y=0 (o
plano zOx) o plano meridiano de P
zOP=zOP".
Para o ponto genérico P indicam-se, na
figura:
c2) Coordenadas cartesianas x, y, z;
simbolicamente
P(x,y,z,)
e2) Coordenadas esféricas  ,r;
simbolicamente P(,r). Em geometria
mede-se  de 0 a 360º positivo no sentido
indicado, e  de 0 a 90º, positivo para z>0
e negativo para z<0. Em Oz  é
indeterminada. (ver longitude geográfica
na figura 03).
Ptolomeu adotara referencial fixo na Terra (Ver #8 A1). Seu sistema astronômico é geocêntrico.
Para corpos celestes resulta uma cinemática sofisticada e, em decorrência, uma Dinâmica
complicada (Newton - Coriolis). Copérnico adotou referencial ligado a estrelas: origem no Sol e
eixos ligados rigidamente a estrelas fixas (Ver #8 A2). Seu sistema astronômico é heliocêntrico. A
Cinemática é simples (Leis de Kepler), a Dinâmica também (Leis de Newton).
#3 - Movimentos Principais da Terra
Adotemos referencial com origem no Sol e eixos ligados a estrelas fixas (Ver #8 A2 e A3).
Constata-se que o globo terrestre executa dois movimentos principais: um movimento diurno e
um movimento anual.
O globo terrestre descreve sua órbita anual em torno do Sol em movimento de translação elíptico
(aproximadamente circular), com período igual a 365,25 dias solares médios.
Simultaneamente, ele executa seu movimento diurno: rotação em torno do eixo diametral SulNorte, com período sideral 86 164 s, período solar 24 h= 86 400 s.
Figura 02 - Movimento de rotação possui velocidade angular . Esta é vetor na
direção do eixo de rotação e sentido determinado pela Regra da Mão Direita. Os
movimentos de rotação e de translação da Terra são concordes em sentido dito
progressivo. Em sentido oposto, o movimento é dito retrógrado (por exemplo a
precessão dos equinócios). O eixo de rotação da Terra é um diâmetro do globo;
suas extremidades são os pólos geográficos Sul e Norte da Terra.
#4
Coordenadas
Geográficas
Equador da Terra é o plano que passa pelo centro e é normal ao eixo Sul-Norte; é o círculo
máximo normal ao eixo.
2
Equador significa "o que divide em partes iguais". Em Geografia o eixo Oz (figura 01) coincide
com o eixo Sul-Norte da Terra (Figura 03); plano-base é o equador. Todo plano que contém o
eixo Sul-Norte é um meridiano.
Na superfície do globo terrestre consideremos um ponto genérico P fora dos pólos. Um particular
ponto G em Greenwich determina o meridiano-de-origem (meridiano zero). As coordenadas
geográficas do ponto P são a sua latitude  e sua longitude  (Figura 03).
Plano meridiano P significa "plano-do-meio-dia" em P, pois o Sol em culminância transpõe o
semi-plano meridiano superior de P ao meio-dia no local.
Figura 03 - Coordenadas geográficas da Terra.
Ponto G no meridiano-de-origem, ponto P genérico (fora
dos pólos) tendo longitude  e latitude . Os arcos medem
ângulos:
Arco P'P = , latitude de P (de 0 a 90º, positiva ao Norte,
negativa
ao
Sul).
Arco G'P' = , longitude geográfica de P (de 0 a 180º,
positiva a W de Greenwich, negativa a E). Na figura é  =
ângulo G'CP'.
Paralelo, como diz o nome, é todo plano paralelo ao equador, logo normal ao eixo Sul-Norte.
A intersecção da superfície do globo terrestre com o plano meridiano é a correspondente linha
meridiana;
com
um
plano
paralelo,
é
a
correspondente
linha
paralela.
Todo ponto P fora do eixo Sul-Norte pertence a um só meridiano e a um só paralelo. Na
superfície do globo terrestre, meridianas e paralelas formam uma rede esférica. São constantes a
longitude
em
cada
meridiana,
a
latitude
em
cada
paralela.
Pode interessar também uma coordenada linear, a altitude de ponto fora da superfície do geóide,
e que se mede na vertical ascendente, a partir da superfície do geóide.
#5 - Esfera Celeste – Eclíptica
Esfera celeste (orbe) é a esfera de raio infinito centrada na Terra ou no Sol, indiferentemente. As
estrelas fixas parecem engastadas na esfera celeste; em conjunto elas constituem o fundo no
qual de projetam os astros móveis (planetas e outros menores), tais como são vistos por
observador na Terra. Salvo expressa declaração contrária, admitimos referencial ligado às
estrelas fixas (Ver #8, A2 e A3).
Para observador na Terra, a projeção do Sol S na esfera celeste é o Sol aparente S'. A Terra e o
Sol aparente são alinhados com o Sol real, de lados opostos deste. O movimento orbital da Terra
e o movimento do Sol aparente têm velocidades angulares iguais em direção, sentido e
intensidade.
Figura 04 - O Plano da figura é o da eclíptica.
Visto da Terra T, o Sol real S projeta-se na
esfera celeste em S' que é o Sol aparente.
3
A órbita terrestre pertence a um plano que contém o Sol S e é fixo na esfera celeste. No mesmo
plano estende-se a órbita do Sol aparente S' na esfera celeste. O citado plano é chamado plano
da eclíptica; qualquer das órbitas citadas é chamada eclíptica.
Eixo Sul-Norte celeste é toda reta fixa paralela ao eixo Sul-Norte terrestre; pode-se imaginá-la
passando pelo centro do Sol. Na esfera celeste ele determina os pólos celestes Sul e Norte.
Equador celeste é todo plano fixo paralelo ao equador terrestre; pode-se imaginá-lo contendo o
centro
do
Sol.
Eixo da eclíptica é toda reta fixa normal a ela; pode-se imaginá-la passando pelo centro do Sol.
Na esfera celeste o eixo da eclíptica determina os pólos celestes austral (ao Sul) e boreal (ao
Norte).
A eclíptica forma com o equador um ângulo diedro (Figura 05); sua aresta é AA'; seu ângulo plano
 é chamado obliqüidade da eclíptica. As medições dão  = 23º 27'. O eixo Sul-Norte e o eixo da
eclíptica formam o ângulo . No ponto A a Terra, na eclíptica, passa de Sul para Norte em 23-set;
o Sol aparente faz isso em 21-mar. Normal à linha AA' concebe-se na eclíptica a linha BB'.
Figura 05 - Posições notáveis da Terra
em sua órbita.
Sejam S e C os centros do Sol e da Terra
respectivamente. O observador, suposto
em C, visa o ponto S. O raio virtual CS
forma com o plano do equador o ângulo 
chamado declinação do Sol. Ela varia
lentamente enquanto a Terra percorre a
sua
órbita.
Latitude de ponto genérico P na
superfície da Terra representa-se por .
A latitude do Sol é chamada declinação e
representada por . Sendo  a
obliqüidade
da
eclíptica,
tem-se
max = + (Terra em B'),  = 0 (Terra em A
ou A'), min = - (Terra em B). (figura 06)
figura 06 - Posições notáveis da Terra em sua órbita.
4
Em A e A' o equador terrestre contém o Sol (d = 0). Em B e B' a declinação do Sol é extremante.
Em resumo:
Posição Posição Declinação
Data
da Terra do Sol do Sol
=
0
21-Mar A'
A,  
21-Jun B'
B,   =  (máx)
23-Set A
A',  
=
0
21-Dez B
B',   = - (mín)
Figura 07 - Considerar pontos P, Q e Q' na
superfície
do
globo
terrestre.
A declinação do Sol é d, considerada constante
durante
um
dia
solar
=
24
h.
Em P o Sol culmina no Zênite (meio-dia em P).
No mesmo instante o Sol está no horizonte tanto
em
Q
como
em
Q'.
Na sucessão das horas, qual é o lugar geométrico
de
P?
O
de
Q?
E o de Q' ?
a) Ponto P: p = , logo p pertence ao intervalo ____. Logo P está na zona Tórrida, entre os
trópicos de Capricórnio (p = , Terra em B) e de Câncer (p = , Terra em B').
b) Ponto Q: Q = (90 - ), com  no intervalo 0____.Q pertence ao intervalo (90º - ____90º. Q
está na calota polar ártica, entre a circunferência polar ártica Q = 90º - ) e o pólo Norte Q =
90º). A Terra está em B').
c) Ponto Q': Analogamente, com Q' = Q' , calota polar antártica, entre Q' = - 90º (pólo Sul) e (90º - ), circunferência polar antártica. A Terra está em B.
Figura
08
Paralelos
notáveis
da
Terra.
Os problemas precedentes mostram que, em cada
latitude, a distribuição da radiação solar pela superfície da
Terra
depende
da
declinação
do
Sol.
Destacam-se na Terra quatro paralelos notáveis.
(1)
Trópico
de
Câncer

=

N
(2)
Trópico
de
Capricórnio

=

S
(3) Círculo polar ártico  = (90º - ) N
(4) Círculo polar antártico = (90º - ) S
Entre os trópicos fica a Zona Tórrida, em cujos pontos o Sol pode culminar no Zênite. Nas calotas
polares o Sol pode incidir rasante.
5
Figura 09- O plano da figura é meridiano. Na
sucessão dos dias, a declinação do Sol é
extremante nas datas indicadas no quadro
abaixo. O Sol culmina no Zênite.
Data
Posição
Posição
da
do Sol
Terra
21 Jun
B'
21 - B
Dez
Local
Estação
da Terra do ano
Trópico
de
B =  .N Câncer
B' =  .S Trópico
de
Capric.
Verão N
Inverno
S
Inverno
N
Verão S
#6 - Precessão da Terra
A eclíptica, e portanto seu eixo, são fixos na esfera celeste. Já o eixo Sul-Norte da Terra e o eixo
Sul-Norte celeste, assim como os planos do equador terrestre e celeste, movem-se lentamente. O
eixo Sul-Norte descreve em torno do eixo da eclíptica um cone de revolução de semiabertura  em sentido retrógrado. É este o movimento de precessão da Terra; seu período é T =
25
790
anos.
O Sol aparente passa pelo ponto A (Figuras 05 -parte1- e 10) em 21-mar, início da primavera no
hemisfério Norte da Terra. Em astronomia este ponto é chamado de "ponto vernal" (do latim: ver,
vernis = primavera); ele é representado pelo símbolo  (signo de Áries, ver #7).
Hiparco (aproximadamente 160 -125 antes de Cristo), fundador da astronomia científica,
localizara o ponto na constelação de Áries. Desde então, devido à precessão da Terra, o
ponto  recuou para a constelação de Peixes.
O ponto A', nas figuras 05 e 10, é chamado de "ponto de outono" (símbolo , signo Libra).
Originalmente ele correspondia a constelação da Libra; atualmente está na constelação da
Virgem.
A reta AA' é chamada linha dos equinócios (ver #10); por isso, o recuo do ponto vernal  é
chamado "precessão dos equinócios".
Os signos do Zodíaco (ver #7) acompanham o ponto vernal , logo sofrem precessão em
relação às constelações. Datas, signos e estações do ano são acoplados de modo imutável.
É desconsiderando o lentíssimo movimento de precessão que se pode afirmar: o eixo Sul-Norte
da Terra executa movimento de translação elíptico (aproximadamente circular) em torno do Sol.
6
Figura 10 - A Terra é um
giroscópio
com
três
movimentos de rotação: o
"spin" (rodopio, movimento
diurno), a precessão e a
nutação. O "spin" tem eixo
de
rotação
Sul-Norte.
Em relação à esfera celeste
o eixo Sul-Norte move-se
lentamente levando consigo
o plano do equador, que lhe
é
normal.
A intersecção AA' do plano
do equador (em precessão)
com o plano da eclíptica
(fixo) gira lentamente em
torno do eixo da eclíptica
(Pólos Austral e Boreal).
A nutação é um floreio da
precessão; presentemente
não interessa.
#7 - Zodíaco. Signos
Do grego: zóon = ser vivo). É na esfera celeste, a zona compreendida entre 8,5º acima e 8,5º
abaixo da eclíptica. Nele se movem o Sol aparente, a Lua, todos os planetas grandes e a maioria
dos pequenos. A partir do ponto vernal  ele é dividido em 12 partes iguais, cada uma se
estendendo por 30º de longitude. A cada parte se atribui um nome e um símbolo: signo do
Zodíaco.
Os signos são designados pelos nomes das constelações que ocupavam suas partes no século II
antes de Cristo (Hiparco).
O Sol aparente penetra no signo de Áries no ponto vernal  em 21-mar. A partir desta data o
ano é dividido em intervalos de aproximadamente um mês cada. Na sucessão destes intervalos o
Sol aparente ocupa respectivamente a sucessão dos signos. Em 23-set o Sol aparente passa
pelo ponto de outono (símbolo) ingressando no signo Libra.
Devido à precessão do ponto vernal  (ver #6), o conjunto dos signos gira lentamente recuando
em relação às constelações. Atualmente correspondem-se:
Signo
Constelação
Áries
Peixes
Libra
Virgem
A reta (-) é o eixo equinocial (AA' nas figuras 05 e 10). Ver #10 - Equinócios.
Signos do Zodíaco
Nome
Áries
Touro
Gêmeos
Câncer
Leão
Virgem
Libra
Símbolo Data
21-Mar.
21-Jun.
23-Set.
7
Escorpião
Sagitário
Capricórnio
Aquário
Peixes
21-Dez.
A seqüência dos signos corresponde à escala de longitudes celestes (ver #8 - A3). A
correspondência imutável entre datas e signos simplifica a explicação dos equinócios (ver #10) e
dos solstícios (ver #11), portanto, das estações do ano.
Figura
11
Seqüência dos signos do
Zodíaco
Áries/Libra
linha equinocial
Câncer/Capricórnio
linha solsticial
#8- Referenciais astronômicos
Adotam-se
coordenadas
esféricas.
Visando
um
astro P na
esfera
celeste,
é r  infinito (coordenada inútil). Restam duas coordenadas angulares. Elas determinam
univocamente a direção na qual, a partir do observador O, se encontra o astro visado.
Apresentamos três referenciais astronômicos, a saber:
A1 - Referencial Horizontal (R.H.)
A2 - Referencial Equatorial (R.Eq.)
A3 - Referencial Eclitical
(R.Ecl.)
A1) Referencial Horizontal.
Seja O qualquer o local do observador na superfície do globo terrestre. Sua latitude seja , com
|| < 90º (por desinteressante, excluímos observador O em pólo geográfico N ou S da Terra).
Plano horizontal em O é o plano tangente ao globo neste ponto. Ele intercepta a esfera celeste no
horizonte de O. A vertical por O contém o centro C do globo terrestre. Na esfera celeste a vertical
determina o Zênite no alto e o Nadir em baixo. O plano do horizonte e o eixo Na - Z são os
elementos essenciais do R.H. emO. Plano vertical que interessa contém a vertical Na - Z do local.
Referencial Horizontal depende do local do observador. Figuras 12 e 13.
8
Figura 12 - Referencial Horizontal. O plano da
figura é o meridiano de O. Ele contém os eixos
coincidentes SN terrestre e ScNc celeste, o local
O do observador e os correspondentes zênite e
Nadir. O plano meridiano de O intercepta o plano
horizontal segundo a reta Sul-Norte local,
tangente à linha meridiana. Na citada reta, os
pontos impróprios Sh e Nh situam-se na esfera
celeste respectivamente ao Sul e ao Norte do
paralelo por O. Fica assim determinada a "Rosa
dos ventos" local em O. Todo plano que contém a
vertical Na - Z é vertical, logo normal ao
horizonte. Interessam dois planos verticais
contendo Na - Z : o meridiano de O e o plano
vertical
pelo
astro
P.
Na figura: T = rotação da Terra em relação à esfera
celeste; E= rotação aparente da esfera celeste em relação à Terra, temse:
E =
- T.
Estando geralmente em outro meridiano, o ponto
P não está representado.
Figura
13
O mesmo Referencial Horizontal em O visto em
perspectiva.
O R.H. em O é transladado para o centro C do
globo terrestre. Ao plano do horizonte fixa-se a
rosa-dos-ventos: pontos impróprios Sh, Nh, E e
W com E - W perpendicular a Sh- Nh
Os arcos medem ângulos. As coordenadas de P
no
R.H.
do
observador
são:
altura
h
=
arco
PP'
azimute
a
=
arco
ShP'
A altura h é medida no plano vertical por P.
Ao invés da altura H, é usual também a distância
zenital (90º - h) = arco ZP.
Visando-se o Sol (com proteção eficiente dos olhos!), seja P o centro do disco solar. A
altura h de P é nula ao nascer-do-Sol (a Este, E, aurora), e novamente ao pôr-do-sol (a Oeste, W,
crepúsculo). A altura do Sol passa por seu máximo (culminância) ao meio-dia local (passagem do
Sol pelo meridiano do observador).
A2) Referencial Equatorial
Ele compõe-se de plano do equador e eixo Sul-Norte da Terra. Ele não depende do local do
observador. Por conter Na - Z e S - N, o meridiano de O interliga os referenciais R.H. e R.Eq. O
plano meridiano de origem contem o ponto vernal .
9
Figura
14
R.H. e R.Eq.
O plano da figura é o plano
meridiano do local do
observador. Ele é elemento
comum aos referenciais
R.H.
e
R.Eq.
O meridiano de O e o plano
do equador interceptam-se
em
CM.
Imagine-se O em C.
O observador em O visa o ponto P na esfera celeste. Pelo ponto P passam os planos: NPS meridiano de P (perpendicular ao equador) e ZPNa - vertical em P (perpendicular ao horizonte).
No R.Eq. as coordenadas de P são:
declinação  = arco TP
ascensão reta  = arco PT
Em particular, a declinação  do Sol depende da posição da Terra em sua órbita. (Ver figuras 08 e
09 - parte1).
É útil também o conceito de ângulo horário - arco TM.
As medições são efetuadas no R.H. e transformadas para o R.Eq. ou para o R. Ecl.
A3) Referencial Eclitical
O observador O é imaginado no centro do Sol. Plano-base é o plano da eclíptica; normal a ele
adota-se o eixo da eclíptica (com pólos austral e boreal).
As coordenadas de P são análogas às terrestres:
latitude celeste 
longitude celeste 
A longitude é medida a partir do ponto vernal .
#9 - Dia e noite. Durações
Seja P na latitude  um ponto na superfície do globo terrestre.
A figura 15(a) está no meridiano de P, e este contém o centro do Sol: é meio-dia em P. A
declinação do Sol é ; ela varia lentamente na sucessão dos dias. A figura 15 representa um
estado da Terra entre as posições A' e B' na figura 05. O segmento de reta PT é a projeção do
paralelo de P no plano da figura.
No globo terrestre, o círculo máximo normal aos raios solares, logo frontal ao Sol, tem traço e e no plano da figura.
O hemisfério voltado para o Sol é iluminado, nele é dia. No outro hemisfério está a sombra da
própria Terra, nele é noite.
A figura 15(b) esta no paralelo de P. A circunferência PVTV'P é a paralela de latitude . Nela é
dia no arcoVPV' = arco 2.VP, é noite em VTV'= arco 2.VT. A rotação da Terra é uniforme, logo a
duração do dia está para a da noite na razão dos arcos VP e VT:
10
duração
----------------------duração da noite
do
dia
=
arco VP
-------------
arco VT
Figura
15(a)
O plano da figura é
o meridiano de P.
Ao meio-dia em P
este plano contém o
Sol; consideremos
este
instante.
Declinação do Sol é
o ângulo d entre o
plano do equador e
o raio Sol-Terra;
este pertence ao
plano da eclíptica.
(Ver Figura 16)
Figura
15(b)
O plano da figura
é o paralelo por
P. VV' é a
intersecção deste
paralelo com o
plano e - e frontal
ao Sol.
Seja o ponto P no hemisfério Norte ( > 0). O segmento PV" cresce com , logo em P a duração
do dia é máxima com max = , o que se verifica na órbita terrestre em B' (Figura 05 - parte 1).
Mutatis mutandis, o exposto se aplica se P estiver no hemisfério Sul: a duração do dia é máxima
com min= - , o que se verifica com Terra em B (Figura 05 - parte 1).
11
Nas estações quentes do ano a duração do dia (com ganho de energia radiante) supera a da
noite, com perda. Nas estações frias dá-se o contrário. Logo, as quatro estações (Primavera,
Verão, Outono, Inverno) decorrem da inclinação  da eclíptica.
Quando a duração do dia é máxima no hemisfério Norte, ela é mínima no hemisfério Sul; e viceversa.
Para o estudo matemático do assunto pode convir o ângulo  entre o raio visual do Sol e o eixo
Sul-Norte; ele é o complemento da declinação do Sol:  = 90º - .
Figura
16
Pontos de tangência
de raios solares
com
o
globo
terrestre.
O círculo máximo
frontal aos raios
solares tem traço e e e circunferência
em cujos pontos o
globo é tangenciado
por raios do Sol.
Os
pontos
de
tangência são as
extremidades
de
diâmetros
de
círculos normais ao
diâmetro e - e, que
é o lugar geométrico
dos centros destes
círculos.
Por exemplo, o
círculo de centro V"
e diâmetro (f - f)
perpendicular (e - e)
é tangenciado em V
e V' por raios
solares
pertencentes a seu
plano.
#10
Equinócios
A palavra significa noites iguais aos dias, em duração.
Previamente analisemos um caso particular: ponto no equador terrestre. Na figura
15(a) P coincide com P', o paralelo PT coincide com o equador P'T'; V" coincide com C. Na
Figura 15(b) V" coincide com C, o segmento VV' torna-se diâmetro do equador. Resulta
arco VP =
arco VT,
logo:
Seja qual for a declinação  do Sol, no equador dias e noites têm durações iguais.
Pergunta-se: De que outro modo pode ser arco VP = arco VT ?
Na Figura 15(a), se for  = 0 (Sol no plano do equador terrestre) o circulo máximo frontal ao Sol
tem traço e- e coincidente com o eixo Sul-Norte da Terra. Resulta PV" = V"T, logo, na Figura
15(b): arco VP = arco VTindependentemente da latitude de . Assim, dia e noite têm durações
iguais em todo ponto fora dos pólos: é equinócio (Ver Figura 06 - parte 1). Isso acontece em duas
posições
da
Terra, A e A' (Figura
17).
12
Os raios solares são normais ao eixo Sul-Norte. No equador terrestre a culminância do Sol se dá
no
Zênite.
Nota: Na tabela abaixo, a notação <=> indica "corresponde a".
Data
Posição Posição
da Terra do Sol
21 - Mar. A'
A <=> 
21 - Jun. B'
B <=> 
23 - Set. A
A' <=> 
21 - Dez. B
B' <=> 
Declinação Estado
do Sol
na Terra
Equinócio Primavera N
=0
Outono S
Solstício
Verão N
 = +
Inverno S
Equinócio Outono N
=0
Primavera S
Solstício
Inverno N
 = -
Verão S
Figura
17
Posições
notáveis
da Terra em sua
órbita.
Ocorrem
os
equinócios em A e
A', os solstícios em
B
e
B'.
(ver Figuras 05 e 06)
#11 - Solstícios.
O termo significa paradas do Sol. Para observador fixo na superfície da Terra, o Sol descreve
diariamente um arco desde o nascente a leste (Este, east, E) até o poente a oeste (Oeste,
west, W). No céu o Sol se eleva até a culminância ao meio-dia (passagem do Sol pelo meridiano
do lugar), e baixa em seguida.
Em dezembro, observador no hemisfério Sul vê o arco descrito pelo Sol em dias sucessivos
conforme a Figura 18 nas datas indicadas; para maior clareza, exageramos as diferenças de dia
para dia.
Até 21-Dez a culminância se eleva, a partir daí ela se abate. Em 21-Dez a culminância não se
eleva mais e ainda não se abate: ela está na altura máxima. O Sol está em  Capricórnio. Esta
parada na variação da culminância do Sol é o solstício de Verão no hemisfério Sul. A declinação
do Sol é a mínima do ano:  = -. Ao meio-dia o Sol está no zênite no Trópico de Capricórnio.(Ver
Figura 06).
13
Figura 20 - (21-Jun) No
trópico de Câncer o Sol
culmina no zênite. No
trópico de Capricórnio o Sol
culmina
com
distância
zenital 2.e N, altura h= (90º
- 2.e). São Paulo fica um
pouco ao Sul do Trópico de
capricórnio; o Sol culmina
com altura h de quase 45º
N, a menor do ano.
(21-Dez) No Trópico de
Capricórnio o Sol culmina
no zênite. No Trópico de
Câncer o Sol culmina com
distância zenital 2.e S,
altura h= (90º - 2.e).
Havana- Cuba, fica um
pouco ao Sul do Trópico de
Câncer; o Sol culmina com
altura h de quase 45º S, a
menor do ano.
#12 - Geometria - Ângulos
Figura 21(a) - Sejam dois planos que se interceptam segundo a reta d. Esta limita quatro semiplanos. Dois destes, por exemplo A e B, formam um ângulo diedro de aresta d; pode-se
representá-lo
por
(AdB).
Figura 21(b) - Plano C normal à aresta d é normal a ambos os planos A e B; é ele secção reta do
diedro (AdB). É em secção reta como C que se mede o ângulo plano do diedro (AdB); é o
ângulo .
14
Figura 22 - Ângulo  entre uma reta r e um plano A. Por r constroe-se o plano D perpendicular
a A; a intersecção destes é a reta i. O ângulo entre r e i é 
Figura 23 - Ângulo diedro em perspectiva. Os retângulos AA'B'B horizontal e AA'C'C inclinado
formam um ângulo diedro cujo ângulo plano é BAC = . Representa-se o segmento AN vertical.
Com o plano horizontal a diagonal r = AC' forma o ângulo B'AC' =  (em perspectiva alterado)
Para obter-se  em verdadeira grandeza, o AB'C' é rebatido em torno do eixo AN, sobre o plano
ABC.
Obtem-se
o AB"C",
no
qual
é=
BAC".
Se for r paralela a AA', r é uma horizontal no plano inclinado, e  = 0. Se for r paralela a AC, é
reta-de-maior-declive no plano inclinado, e  = . Exceto nestes casos limites, com r qualquer no
plano inclinado é < . Em geral 0 <=  <= .
Na esfera celeste, com equador horizontal a eclíptica é inclinada; estes planos formam o ângulo
diedro . O eixo S-N é paralelo ao segmento AN na figura supra. Sejam S e T os centros do Sol e
da Terra respectivamente. Imaginar S em A e T em C'. O rio de luz solar ST = r pertence à
eclíptica. O ângulo deste raio com o equador é a declinação  do Sol.
Em particular:
Equinóxios ST
= r na
aresta
do
diedro,  =
0
Solstícios - ST = r é reta-de-maior-declive na eclítica  = 
#13 - Raio da terra - Heron de Alexandria
No século I d.C. viveu em Alexandria um grego, matemático e físico de nome Heron. Ele fôra
informado de que em Assuan, em certo dia do ano, o Sol em culminância se refletia na água no
fundo de um poço. Sabendo que Assuan e Alexandria se situavam aproximadamente no mesmo
meridiano separados por distância d, Heron concebeu um modo de calcular o raio R do globo
terrestre. Ver esquema abaixo:
15
Na mesma data, em Alexandria, Heron mediu a sombra s de um poste vertical de altura a.
Presumindo que seja  um ângulo pequeno, os triângulos são aproximadamente semelhantes,
logo:
Heron obteve resultado bem próximo do correto. Um milênio e meio após, Colombo teve
dificuldade em convencer seus contemporâneos que a Terra é redonda!
16