otimização do tratamento farmacológico de pacientes hiv

OTIMIZAÇÃO DO TRATAMENTO FARMACOLÓGICO DE
PACIENTES HIV-SOROPOSITIVOS
Leno Silva Rocha
Instituto Tecnológico de Aeronáutica – Praça Marechal Eduardo Gomes, 50, Vila das Acácias, CEP 12228-900.
São José dos Campos - SP – Brasil.
Bolsista PIBIC-CNPq
[email protected]
Cairo Lúcio Nascimento Júnior
Instituto Tecnológico de Aeronáutica – Praça Marechal Eduardo Gomes, 50, Vila das Acácias, CEP 12228-900.
São José dos Campos - SP – Brasil.
[email protected]
Diferentes esquemas de tratamento de pacientes HIV+ são adotados ao redor do mundo. Busca-se, neste
trabalho, aperfeiçoar protocolos de tratamento, respeitando-se restrições biofísicas e seguindo critérios do consenso
brasileiro e da OMS relativos à administração de drogas anti-virais. Aplica-se técnicas de otimização a um modelo
matemático da dinâmica do vírus HIV, de modo que se encontram esquemas ótimos de tratamento farmacológico. Os
resultados são comparados sob uma óptica primordialmente teórica, que mais objetiva discutir vantagens e possíveis
pontos de melhoramento em terapia anti-retroviral. A viabilidade de um projeto de aparelhagem para controle
contínuo é analisada, tendo em vista a questão da aderência ao tratamento. Conclui-se que os benefícios conquistados
com o controle mais assíduo da dosagem são relativamente pequenos. Além disso, é inviável o projeto de aparelhagem
médica de controle contínuo. A freqüência de controle do protocolo mais vantajoso, encontrado teoricamente,
coincidiu com o padrão utilizado na Brasil.
Palavras chave: Controle ótimo, tratamento, HIV, métodos numéricos, otimização.
1. Introdução
Desde a descoberta da Aids e do vírus HIV (sigla inglesa de Vírus da Imunodeficiência Humana) na
década de 1980, diversos desafios científicos, sociais e políticos têm suscitado. Segundo dados da ONU
(Organização das Nações Unidas), no ano de 2006 existiam 39.5 milhões de casos registrados de portadores
do vírus HIV no mundo e taxa crescente de novos casos. O Boletim Epidemiológico Brasileiro registra
433.067 casos de Aids no território nacional no ano de 2005 com tendência à estabilização desse número,
graças ao avançado Programa Nacional de DST/Aids (DST - Doenças Sexualmente Transmissíveis).
Este cenário, agravado pelo caráter crônico da patologia, ratifica a imprescindibilidade não apenas de
buscar métodos de cura da doença, mas também de persistir nas linhas de controle da propagação do vírus e
do aperfeiçoamento nos tratamentos de pacientes soropositivos e doentes. O presente trabalho segue esta
última vertente, utilizando um modelo matemático básico de dinâmica viral, simulação computacional e
algoritmos de otimização.
Essa metodologia permite encontrar dosagens que aperfeiçoam tratamentos levando-se em conta
índices de desempenho definidos a priori. Tais índices, ou funções custo, representam o compromisso entre
maximização de resultados terapêuticos e minimização de efeitos colaterais, respeitando-se um conjunto de
restrições biofísicas do organismo submetido à intervenção.
Assim, foram obtidos esquemas de administração de droga com suas respectivas dosagens ótimas e
valores de índice de desempenho no horizonte de tempo de um ano. Em seguida, refinou-se a partição
temporal sucessivamente até chegar à posologia mensal, passando por outras quatro estratégias de
tratamento menos refinadas incluindo a semi-realística com dosagens constantes fixadas a cada dois meses.
Observou-se que o refinamento temporal traz melhorias percentuais baixas nos índices de
desempenho. Entretanto, comprova-se que esse diminuto percentual é típico dessa abordagem na classe de
problemas de otimização. Para os pacientes com estado pré-tratamento não agravado, isto é, com
concentração sanguínea de CD4 ≥ 350 células/mm3, não se esperam melhorias significativas com esquemas
de tratamento mais minuciosos de controle. Porém, para indivíduos com CD4 abaixo dessa concentração,
protocolos aperfeiçoados podem diminuir a gravidade do quadro, e representar menor bombardeamento
fármaco.
1
2. Matemática da Dinâmica Viral
O modelo matemático adotado foi proposto por Nowak et al.(1996), para descrever a dinâmica do
vírus HIV em organismos humanos. As hipóteses assumidas nessa modelagem podem ser consultadas no
artigo “Population Dynamics of Immune Responses to Persistent Viruses”. O modelo consiste em um
sistema de quatro equações diferenciais ordinárias não-lineares, que descreve especificamente a variação
das grandezas: x - quantidade de células CD4 saudáveis; y - número de células CD4 infectadas; v –
quantidade de vírus livre; e z – número de linfócitos T citotóxicos específicos ao antígeno HIV, designados
CTL (Cytotoxic T Lymphocytes); em função do tempo t ∈ R+:
dx ( t )
= λ − Dx ( t ) − β ( t ) x ( t ) v (t )
dt
dv ( t )
= k (t ) y (t ) − u (t ) v ( t )
v& =
dt
d y (t )
y& =
= β (t ) x (t )v (t ) − a y (t ) − p y (t ) z (t )
dt
d z (t )
= c y (t ) z (t ) − b z (t )
z& =
dt
x& =
(1)
As condições iniciais, bem como os parâmetros intervenientes, obedecem ao conjunto de restrições
biofísicas e foram adotados conforme tabela apresentada por Yoneyama et al. (1999).
Tabela 1. Valores dos parâmetros do modelo usados na simulação computacional.
Parâmetros
Valores Parâmetros Valores
λ
1.0
b
0.01
D
1.0
c
0.1
a
0.8
u
0.01107
p
0.05
k
1.0
•
•
•
•
•
•
•
•
•
O parâmetro λ corresponde à constante de produção de células não infectadas;
D é a taxa de mortalidade das células não infectadas;
a é a taxa natural de morte de células infectadas;
β (t) é a taxa de infecção de células CD4 saudáveis pelo vírus HIV;
p representa a taxa de declínio das células infectadas devido ao contato com vírus;
b é a taxa de decadência de CTLs;
c é o índice de produção de CTLs;
u (t) corresponde à mortalidade viral;
k (t) quantifica a produção de vírus livre.
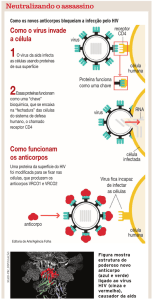
Figura 1. Aspectos quantitativo-esquemáticos da replicação do vírus HIV.
A amenização dos efeitos patológicos ligados ao HIV é alcançada por meio de diversas drogas,
dentre elas as anti-retrovirais. O Ministério da Saúde (2007) brasileiro disponibiliza 17 medicamentos antiHIV, que combinados geram vários esquemas de tratamento. Neste trabalho, todavia, a única droga
adjuvante é o zidovudine (AZT), primeiro fármaco eficaz contra a progressão da imunodeficiência, em uso
desde o fim da década de 80.
Para cada posologia adotada, os resultados finais do tratamento são avaliados conforme funções
custo definidas previamente. Desta forma, tem-se um problema de controle ótimo, conforme caracterização
de Kirk (1970), com formulação matemática consistente, restrições físicas pertinentes e índice de
desempenho a ser minimizado.
2
3. Atividades Realizadas
A atuação de uma massa de droga num instante de tempo t, designada por m(t), no sistema biológico,
é bem expressa pela relação exponencial com o parâmetro beta, conforme Yoneyama et al. (1999):
β(t) = exp ( -m(t) )
(2)
A variável m(t) é uma função m: [0,12] → R representada discretamente por meio de vetor que
apresenta a dosagem progressivamente no tempo da direta para a esquerda, aproximando instantes
temporais por intervalos nos quais as dosagens se mantêm constantes. Inicialmente utilizou-se dosagem
constante ao longo de todo o ano, para obter o protocolo anual, empregando-se busca unidimensional
através do método de Dichotomous, cuja descrição pode ser consultada no livro de Wismer (1979),
“Introduction to Nonlinear Optimization”.
Além desse protocolo, outros cinco modos de particionamento temporal foram adotados: semestral
em dois semestres; quadrimestral com três quadrimestres; trimestral com quatro trimestres; bimestral com
seis bimestres; e mensal com doze meses.
Nos esquemas bimestral, quadrimestral e trimestral, utilizou-se busca multidimensional pelo método
dos Poliedros Flexíveis. Essa técnica encontra-se no livro de Press et al. (1992) “Numerical Recipies In C”.
Todos os processos citados até aqui são de ordem zero, isto é, não envolvem derivadas na busca pelos
extremos.
O esquema bimestral é uma estratégia semi-realística de tratamento, pois corresponde à aproximação
teórica do procedimento padrão do sistema público de saúde nacional: o paciente em tratamento é avaliado
clinicamente a cada dois meses e se submete a exames laboratoriais a cada três meses. Cumpre ressaltar
que na prática os esquemas de tratamento são personalizados e seguem o consenso do Ministério da Saúde.
Nos modos bimestral e mensal de administração farmacológica o algoritmo de otimização
empregado foi o Steepest Descent, que é descrito por Kirk (1970), em “Optimal Control Theory”. Ao
contrário das rotinas usadas até o nível trimestral, esse algoritmo embasado no Cálculo Variacional é mais
complexo e envolve o uso de derivadas. Por isso, serão descritos detalhes do trabalho desenvolvido com
essa teoria.
Dois índices de desempenho foram escolhidos seguindo a literatura especializada, com o intuito de
manter um padrão que permita comparações com outros trabalhos científicos já realizados, sem, contudo
desviar do objetivo de aperfeiçoamento dos esquemas de intervenção farmacológica. As funções custo são:
J (F ) = F.
v 2 (t f )
2
J (G, H ) = G.
tf
+∫
t0
y 2 (t f )
2
m2 ( t )
2
+ H.
dt
(3)
v 2 (t f )
2
tf
+ ∫ m 2 (t )dt
(4)
t0
Em J(F), leva-se em conta a redução da carga viral v(t) no instante final do tratamento e a redução de
efeitos colaterais, vinculados à integral do quadrado da variável de controle m(t) em relação ao tempo. Já
no custo J(G,H) considera-se também a diminuição da carga final de células CD4 infectadas. Os fatores F,
G e H são pesos ponderados que dependem de avaliação subjetiva da relativa importância dos efeitos
adversos, da redução da carga viral e da quantidade final de células infectadas. A avaliação deve ser feita
com o apoio de especialistas para obtenção de análises precisas de modo a aproximar os resultados teóricos
dos casos reais de maneira confiável.
Variados pesos foram utilizados e os resultados vinculados a cada valor de ponderação foram
tabelados. Os índices de desempenho não têm significado físico e são adimensionais, conforme Kirk
(1970), pois contam com combinações de diferentes grandezas físicas. Visando à simplicidade, também se
considera que os pesos de ponderação são desprovidos de unidades.
Reescrevendo as Eqs. (1) na forma matricial, obtém-se o Hamiltoniano para os casos relativos,
respectivamente, às funções de custo J(F) e J(G,H):
Η1 =
m 2 (t )
+ [ g1 ( t )
2
g 2 (t )
g 3 (t )
g 4 (t ) ] . [ x
v
3
y
T
z]
(5)
Η 2 = m 2 (t ) + [ w1 (t ) w2 (t ) w3 (t ) w4 (t )] .[ x v
y
T
z]
(6)
Os vetores de coestado g(t) e w(t) contêm os multiplicadores de Lagrange para cada situação e
fornecem equações de coestado, por meio da diferenciação dos Hamiltonianos em relação ao vetor de
estado, invertendo-se o sinal das expressões obtidas. O sistema de equações de coestado abaixo é referente
ao custo J(F). O argumento de tempo dos multiplicadores foi omitido para não sobrecarregar a notação:
g& 1
g& 2
g& 3
g& 4
= g 1 ( D + β ( t ) v ( t )) − g 3 β ( t ) v ( t )
= g 1 β (t ) x (t ) + g 2 u (t ) − g 3 β (t ) v (t )
= − g 2 k ( t ) + g 3 ( a + p z ( t )) − g 4 c z ( t )
= g 3 p y ( t ) + g 4 ( − cy ( t ) + b )
(7)
Os índices de desempenho escolhidos são distintos, porém a lei de coestado é a mesma para os dois
problemas. Desta forma, basta reescrever o sistema de Eqs. (7) substituindo as letras “g” por “w” e ter-se-á
o sistema de coestados relativo ao segundo custo proposto.
O valor ótimo da variável de controle a cada instante é encontrado empregando-se o princípio do
mínimo de Pontriagin. Este princípio relaciona-se à minimização do Hamiltoniano, como explica Kirk
(1970). A aplicação dessa metodologia envolve complicações na solução geral do problema não-linear, por
isso se torna necessário lançar mão de métodos numéricos. A propagação das equações diferenciais foi
realizada com o integrador Runge-Kutta de quarta ordem, através da função ode45 do software MATLAB.
Com a técnica do steepest descent, avalia-se o resíduo de ∂Η / ∂m, compelindo a variável de controle a
se aproximar sucessivamente da condição necessária de optimalidade:
∂Η
=0
∂m
(8)
A integração das equações de coestado é reversa no tempo, isto é, ocorre a partir do instante final
(t=12) até o instante inicial (t=0). Portanto, as condições iniciais nessa situação são na verdade condições
terminais de coestado dadas pela diferenciação dos custos em relação ao vetor de estado:
g ( t f ) =  0
w ( t f ) =  0
F .v ( t f )
H .v ( t f )
0
0 
G . y (t f )
T
(9)
0 
T
(10)
O a rotina implementada converge rapidamente nos estágios iniciais, contudo à medida que é
diminuído o Hamiltoniano, a velocidade de convergência se reduz drasticamente. Além disso, a boa
calibração dos parâmetros, como critérios de parada e tolerâncias, é crucial, pois caso contrário, oscilações
severas podem ocorrer, fazendo com que o método sequer convirja.
A escolha inicial do vetor de controle não tem importância tão significativa na convergência do
método, todavia os índices de desempenho ótimos têm valores muito próximos e a questão da inicialização
acaba desempenhando papel importante na melhoria percentual dos tratamentos. Por isso, sugere-se
investigações futuras sobre essa questão, aplicando-se métodos que transpassam dificuldades relativas à
existência de vários extremos locais.
Além disso, a vetorização da variável m(t) inviabiliza a escolha do melhor vetor inicial por tentativa,
pois o número de combinações de dosagens competitivamente candidatas no espaço multidimensional é
infinito no conjunto de valores aceitáveis como dosagem. A técnica “simulated annealing” descrita no livro
“Numerical Recipes in C” é uma opção conveniente para realização dessa tarefa.
4. Resultados Obtidos
Admitiu-se que: a aderência à terapia é total; a absorção é alta; o organismo é virgem de tratamento e
assim não há tolerância, nem falha virológica; não há uso concomitante de outras drogas. Estas hipóteses
garantem uma farmacocinética favorável à simulação e elimina complicações na abordagem teórica.
4
4.1 – Valores dos custos e comparação dos mesmos
Os valores ótimos encontrados para as massas de fármaco a serem administradas foram truncados, e
substituídos pelos múltiplos de 10 mais próximos. Isto torna os tratamentos ótimos teóricos obtidos mais
factíveis, considerando-se que a maioria dos tratamentos é desenvolvida com comprimidos e cápsulas.
Desta forma, o preparo de massa por fracionamento de comprimido fica plausível. Esse procedimento
numérico nos valores de massa justifica também a omissão das incertezas relativas às dosagens.
A grandeza custo, com seu(s) respectivo(s) peso(s) de ponderação e dosagens ótimas, obtida nos
tratamentos bimestral e mensal é apresentada a seguir:
Tabela 2. Resultados: tratamento bimestral e índice J(K).
K
J(K)
Dosagem ótima (mg)
1
10
50
100
300
500
26.44
62.52
116.78
160.38
290.63
400.52
180
270
340
380
450
480
170
270
340
380
450
480
170
270
350
380
450
480
160
270
340
380
450
480
160
260
340
380
450
480
140
250
320
360
430
460
Tabela 3. Resultados: tratamento mensal e índice J(K).
K
J(K)
Dosagem ótima (mg)
1
10
50
100
300
500
26.72
62.49
116.63
160.06
289.91
400.10
180 180 180 170 170 170 170 160 160 150 130 90
260 260 270 270 270 260 260 260 260 260 250 230
340 340 340 340 340 340 340 340 340 340 330 290
370 380 380 380 360 380 380 380 380 370 360 320
440 450 450 460 450 450 450 450 450 450 430 400
480 480 480 490 490 490 490 480 480 480 470 440
As taxas de variação percentual entre esquemas de tratamento sucessivamente refinados no tempo,
bem como as características dos protocolos, foram tabeladas e curvas de comparação foram traçadas.
Tabela 4. Comparação dos índices ótimos J(1) obtidos em diferentes partições de tempo.
Divisão do horizonte
Nomenclatura
Custo J(1)
Variação relativa ao índice
Principal técnica de
do tratamento
precedente
minimização empregada
1
2
3
4
6
12
Anual
Semestral
Quadrimestral
Trimestral
Bimestral
Mensal
27.2
27.0
26.9
26.8
26.4
26.7
0.74%
0.37%
0.37%
1.52%
-1.12%
5
Busca de Dichotomus
Poliedros Flexíveis
Poliedros Flexíveis
Poliedros Flexíveis
Steepest Descent
Steepest Descent
Figura 2. Curvas de variação percentual de custos sucessivos para diferentes ponderações.
A tabela do segundo tipo de custo revela taxas da ordem de décimos de percentual, semelhantemente.
Tabela 5. Comparação dos índices ótimos J(30,100) obtidos em diferentes segmentações temporais.
Divisões de tempo
Custo J(30,100)
Variação percentual relativa
Principal técnica de
ao índice precedente
otimização empregada
1
2
3
4
6
12
235.1250
234.7488
234.3824
234.0937
234.0686
233.5725
0.16%
0.16%
0.12%
0.01%
0.21%
Busca de Dichotomus
Poliedros Flexíveis
Poliedros Flexíveis
Poliedros Flexíveis
Steepest Descent
Steepest Descent
Analisando-se os esquemas de tratamento correspondentes, nota-se que a diminuição relativa dos
índices de desempenho é muito pequena. Entretanto, essa é uma característica comum na classe de
problemas de otimização, como se constata na seção 4.5.
4.2 – Discussão sobre o índice J(1)
A curva do índice de desempenho com peso de ponderação unitário tem um comportamento diferente
em relação às demais. Sua topologia conta com o trunfo de um máximo global. Por outro lado, um mínimo
global com valor negativo também aparece, fato imprevisto na teoria, mas que pode ser explicado conforme
os próximos parágrafos. A explicação, entretanto, não afasta a conveniência de se pesquisar novos meios de
reduzir esse custo, nem elimina a necessidade de maiores investigações sobre o fato.
O gráfico seguinte mostra as curvas do quadrado da carga viral no tempo. Essa grandeza é referente à
primeira parcela do índice J(1).
6
Figura 3. Evolução do quadrado da concentração de vírus livre.
A trajetória do tratamento mensal revela que a concentração de viral é, no instante final, maior que
nos esquemas menos refinados. Por isso, a redução dos efeitos colaterais no índice J(1) mensal, mostrada
na Fig. 3, não compensa o nível de vírus livre ao final do tratamento. Assim, o controle mês a mês
proporciona um custo maior em relação ao bimestral, resultando na taxa de variação de -1.12% apresentada
na Tab. 4.
Figura 4. Representação da acumulação de efeitos colaterais ao longo do tempo.
4.3 – Análise da variação dos índices
A maior taxa de variação do tratamento anual para o mensal, foi 1.87% com J(1). Em seguida vem o
valor de 0.96%, alcançado com o índice J(10). Esses números trazem a indagação: que benefícios os
pacientes podem ganhar com variações tão baixas? Os benefícios dependem do estado indivíduo portador
do vírus antes do início da terapia.
7
O consenso nacional do ano de 2006 recomenda o início do tratamento anti-retroviral em duas
situações. A primeira delas é o quadro com manifestações clínicas associadas ao HIV. A outra é referente à
contagem de CD4 pré-tratamento abaixo de 350 células/mm3.
Suponha que um paciente tenha 100 CD4/mm3. Com essa concentração, ele provavelmente terá
infecções oportunistas e deverá tomar mais remédios além do anti-retroviral. Nesse sentido, a otimização
não propicia apenas a vantagem de redução menor que 2% no consumo de AZT, mas envolve uma alta
probabilidade de diminuição de efeitos adversos relativos às outras medicações, eventualmente necessárias.
4.4 – Viabilidade de aparelhagem para tratamento de pacientes HIV – soropositivos
Vários produtos de engenharia biomédica são comercializados em pequena escala para uso particular.
Nesse mercado individualizado pode-se encontrar desde termômetros digitais, até relógios frequencímetros
de ritmo cardíaco, e instrumentação portátil para medidas de glicemia e infusão de insulina.
Estes aparelhos portáteis têm em comum a característica de permitir o monitoramento ou o controle
de processos biológicos que podem, em curto prazo, acarretar diversos danos à saúde. Tais prejuízos podem
ser menos significativos, como indisposição e fadiga; podem ser problemas mais sérios, como desmaios; e
podem até ser danos irreversíveis, como desnaturação protéica.
A aparelhagem anti-HIV, que propiciaria o tipo de tratamento proposto nesse trabalho deve ser como
as “bombas de infusão de insulina”, usadas por diabéticos no Brasil desde 1998. Esses aparelhos injetam
continuamente doses de insulina no paciente, ficando conectados ao corpo do usuário 24 horas por dia, pois
o diabetes é uma doença crônica, assim como Aids/HIV. Os equipamentos de insulina têm dimensões
próximas a de um cartão de crédito, exceto os cerca de 3 centímetros de espessura. O peso não passa de um
newton e ligam-se ao corpo por cateter com agulha flexível na extremidade.
Diferentemente das situações, para as quais há equipamentos individuais de engenharia biomédica,
os problemas clínicos no caso de infecção pelo HIV, não ocorrem em curto prazo. Desta forma, nem o
monitoramento nem o controle imediato de processos biológicos são essenciais para a preservação da
estabilidade, ou mesmo reversão do quadro de um paciente.
As principais características iniciais da idealizada “bomba anti-HIV” foram estimadas para que se
pudesse confrontá-las com as peculiaridades das bombas de infusão de insulina. Assim, a comparação entre
os fatos do produto existente e as previsões do futuro produto permitem avaliar se os critérios iniciais de
viabilidade do projeto são satisfeitos. Caso esses critérios fossem aprovados, avançar-se-ia para uma etapa
com a análise mais detalha de parâmetros de engenharia e preços de um protótipo.
Tabela 6. Avaliação de vantagens e desvantagens da Bomba de Insulina e da Bomba anti-HIV.
Aparelho
Bomba de insulina
Bomba anti-HIV
Evento
(fatos)
(previsões)
Aumenta a eficácia do tratamento
Sim
Sim
Facilita muito a administração de substâncias do
Sim
Não
tratamento
-Evita o uso constante de seringa-Fármacos não injetáveisEvita pioras repentinas (em questão de horas) no
Sim
Não
quadro do paciente
-Característica do diabetes-Dinâmica viral não imediataLoop fechado
Não
Dificilmente
Preço baixo (menos que mil reais)
Não
Dificilmente
Evita problemas futuros de:
-Absorção de insulina-Resistência ao fármacoSim
Sim
Alta probabilidade de aumentar a aderência à terapia
Sim
Sim
A conjuntura mostrada no quadro aliada aos resultados de redução dos índices de desempenho, nas
diferentes posologias, não traz motivação para o desenvolvimento de um projeto de aparelhagem médica
visando ao controle farmacológico contínuo no tempo para tratamento de pacientes portadores do vírus
HIV.
4.5 – Analogia entre situações
O refinamento de partições objetivando melhorias na abordagem numérica de problemas envolvendo
otimização e a dicotomia entre o contínuo e o discreto geralmente não conduz a elevadas taxas de mudança
percentual em suas grandezas características, considerando-se intervalos de variação relativamente
8
pequenos. O exemplo apresentado a seguir corrobora com essa idéia e mostra como a administração ótima
de fármacos no tratamento de pacientes HIV+ leva, em geral, a níveis de melhoria percentuais maiores que
os normalmente obtidos nessa classe de problema.
4.5.1 – Otimização do lucro em juros compostos
Suponha que uma soma de dinheiro seja depositada em uma entidade que paga juros à taxa anual r. O
valor do investimento S(t), em qualquer instante t>0, depende da freqüência na qual o juro é capitalizado e
também da taxa de juros. Admitindo-se essa capitalização como contínua, o problema de valor inicial que
descreve o crescimento do investimento feito é dado pelas equações:
dS
= rS
dt
S (0) = S 0
(11)
(12)
Cuja solução é a fórmula exponencial dada por:
S ( t ) = S 0 e r .t
(13)
A situação na qual a capitalização ocorre em intervalos finitos de tempo suscita por meio do
raciocínio subjacente. Se o juro for capitalizado uma vez por ano, então depois de t anos:
S (t ) = S0 (1 + r )t
(14)
Se o juro for capitalizado duas vezes por ano, então depois de seis meses o deposito inicial fica
multiplicado pelo fator [ 1 + (r/2) ] e no final do ano o montante passa a ser o valor inicial vezes o fator
[ 1 + (r/2) ]2. Portanto,
 r
S (t ) = S 0  1 + 
 2
2.t
(15)
Em geral, se os juros forem capitalizados m vezes durante o ano, então:
r

S (t ) = S 0  1 + 
 m
m .t
(16)
Os resultados dos casos discretos são dados na Tab.6, para uma taxa de juros r = 8 % a.a.
Tabela 7. Crescimento do investimento à taxa de juros r = 8% ao ano, com vários modos de capitalização.
m
Índice S(1)/S(0) Eq.(6)
Variação percentual em
(adimensional)
(adimensional)
relação ao índice precedente
1
1.0800
2
1.0816
0.15 %
3
1.0822
0.06%
4
1.0824
0.02%
6
1.0827
0.02%
12
1.0830
0.03%
O índice S(1)/S(0) no caso contínuo vale 1.0833 e implica em uma variação percentual de 0.03% em
relação à partição do ano em doze intervalos iguais.
9
Figura 5. Curvas de melhoras percentuais nos processos de cobrança de juros e no tratamento de pacientes
HIV - soropositivos.
5. Conclusões
A avaliação dos índices nos diversos protocolos de tratamento permite concluir que tanto para os
custos J(F), como para os J(G,H), os protocolos mais refinados no tempo implicam em melhores resultados
numéricos finais, apesar da diferença não ser expressiva e com exceção do tratamento J(1) mensal.
As dosagens nos diferentes esquemas de tratamento ficaram condizentes e nota-se que é vantajoso
administrar maior massa de drogas inicialmente e em seguida reduzir a dosagem, resultado coerente com o
artigo de Yoneyama et al., 1999. Em todas as posologias mais refinadas que a anual, o primeiro valor a ser
administrado é maior que o último.
O fato de o controle imediato de processos biológicos, na fase sintomática em questão neste trabalho,
ser desnecessária aliado à baixa redução nos índices de desempenho se contrapõem à viabilidade de um
projeto de aparelhagem médica visando ao controle farmacológico contínuo no tempo para tratamento de
pacientes soropositivos.
6. Agradecimentos
Ao CNPq – Conselho Nacional de Desenvolvimento Científico e Tecnológico pelo apoio financeiro;
aos professores Cairo e Takashi do ITA; à psicóloga Edilamar do COAS (Centro de Orientação e Apoio
Sorológico) de São José dos Campos; e à infectologista Eni coordenadora do Programa de Aids/DST de
São José dos Campos.
7. Referências
Caetano, M.A.L; Souza, J.A.M.F. & Yoneyama, T., 2003, “A model based analysis of AIDS treatment”,
Proceedings of The Western Multiconference on Health Sciences Simulation, Orlando, USA, pp 6570.
Caetano, M.A.L. & Yoneyama, T., 1999, “Comparative Evaluation of Open Loop and Closed Loop Drug
Administration Strategies in the Treatment of AIDS”, Anais da Academia Brasileira de Ciências,Vol.
71, No. 4-I. 589-597.
Caetano, M.A.L. & Yoneyama, T., 1999, “Optimal Control Theory Applied to the Anti-Viral Treatment of
AIDS”, Theory and Mathematics in Biology and Medicine Conference, Amsterdam, Netherlands.
Camargo, K., 2005, “AIDS Vinte Anos- Esboço histórico para entender o Programa Brasileiro” adaptado
por Pedro Chequer, ex-diretor do Programa Nacional de DST/Aids.
ONU, 2006.“Global Summary of the AIDS Epidemic”, Relatório do Programa das Nações Unidas para
AIDS, Dec. 2006.
10
Kirk, D.E., 1970. “Optimal Control Theory”, An introduction. Prentice-Hall New York.
Ministério da Saúde, ano III, Dezembro de 2006, “Boletim Epidemiológico- Aids e DST”.
Nowak, M.A. & Bangham, R.M., 1996, “Population Dynamics of Immune Responses to Persistent
Viruses”, Science, Vol. 272, Apr.5, pp 74-79.
Press, W.H.; Teukolsky, S.A.; Vetterling, W.T. & Flannery B.P., 1992. “Numerical Recipes in C”, The Art
of Scientific Computing, 2nd Edition. Cambridge University Press.
SBD (Sociedade Brasileira de Diabetes), 2006, “Desvendando a bomba de insulina”, Revista Mais Saúde,
Edição no 23.
Wismer, D. & Chattergy, 1979. “Introduction to Nonlinear Optimization”, A problem solving approach.
Elsevier North Holland, Inc.
WHO (World Health Organization), 2006, “Antiretroviral therapy for HIV infection in adults and
adolescents: recommendations for a public health approach”.
11