bloco 13

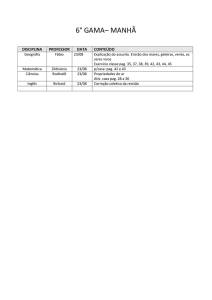
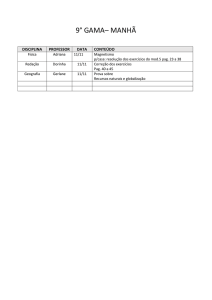
Estabilidade Interna
1.
Estabilidade Interna
2.
Análise de Estabilidade Segundo Lyapunov
3.
Teorema de Lyapunov
4.
Teorema de Lyapunov – Caso Discreto
c Reinaldo M. Palhares
°
pag.1
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna
Veja que a BIBO estabilidade é definida para a resposta ao estado inicial nulo.
Para se estudar a resposta à entrada nula, considere o sistema autônomo:
ẋ(t) = Ax(t)
com uma condição inicial não nula x0 . A solução é dada por: x(t) = eAt x0
B Um ponto de equilı́brio é alcançado quando ẋ(t) ≡ 0
B No caso contı́nuo, todas as derivadas nulas significam que os estados não
estão variando no tempo e portanto, são indicados como estados ou ponto de
equilı́brio, xe
c Reinaldo M. Palhares
°
pag.2
Teoria de Sistemas Lineares – Aula 13
Análise de Estabilidade Segundo Lyapunov
Estabilidade no sentido de Lyapunov
todos os pontos tais que
kx0 − xe k ≤ ν,
ν>0
Seja R(ν) a região que consiste de
→ x0 = estado inicial
e seja R(ε) a região que consiste de todos os pontos tais que
kx(t) − xe k ≤ ε,
ε > 0, ε > ν
∀t > 0
B Um estado de equilı́brio, xe , do sistema autônomo é dito estável no sentido
de Lyapunov se, correspondendo a cada R(ε) houver um R(ν) tal que toda
trajetória iniciada em R(ν) está confinada em R(²) à medida que t cresce
c Reinaldo M. Palhares
°
pag.3
Teoria de Sistemas Lineares – Aula 13
Análise de Estabilidade Segundo Lyapunov
Estabilidade Assintótica Um estado de equilı́brio, xe , do sistema autônomo é
dito ser assintoticamente estável se for estável no sentido de Lyapunov e se
toda solução começando em R(ν) converge para xe , sem deixar R(ε), a medida
que t aumenta
Instabilidade Um estado de equilı́brio do sistema autônomo é dito ser instável
se, para algum escalar ε > 0, e todo escalar ν > 0, há sempre um estado x0 em
R(ν) tal que a trajetória iniciando neste estado deixa a região R(ε)
c Reinaldo M. Palhares
°
pag.4
Teoria de Sistemas Lineares – Aula 13
Ilustração das definições
x1
ε
x0
ν
t
x0
x2
trajetória assintoticamente estável
x1
ε
x0
x0
ν
x2
x0
trajetória assintoticamente estável
c Reinaldo M. Palhares
°
pag.5
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna
Veja que a definição de estabilidade neste caso pode ser operacionalizada da
forma:
Teorema A equação ẋ(t) = Ax(t) é marginalmente estável se e somente se
todos os autovalores de A têm parte real igual a zero ou negativa e aqueles que
têm parte real igual a zero são raı́zes de multiplicidade 1 do polinômio mı́nimo
de A
Teorema A equação ẋ(t) = Ax(t) é assintoticamente estável se e somente se
todos os autovalores de A têm parte real negativa
c Reinaldo M. Palhares
°
pag.6
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna
B As transformações de equivalência não afetam a estabilidade de uma equação
de estado... Definindo x̄ = P x, com P não singular, ẋ = Ax é equivalente a
x̄˙ = Āx̄ = P AP −1 x̄
B Como P é não singular, se x é limitado, então x̄ também o é; se x tende a
zero quando t → ∞, o mesmo ocorre com x̄
B A estabilidade de A pode ser estudada através de Ā
c Reinaldo M. Palhares
°
pag.7
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna
A solução de x̄˙ = Āx̄ para x̄(0) é dada por x̄(t) = eĀt x̄(0). Se Ā está na
forma de Jordan, pode-se mostrar que:
B Se um autovalor tem parte real negativa, cada elemento do bloco de Jordan
associado é limitado e tende a zero quando t → ∞
B Se um autovalor tem parte real igual a zero e nenhum bloco de Jordan de
ordem 2 ou maior, então o elemento correspondente é constante ou senoidal para
todo t e portanto limitado
B Se um autovalor tem parte real positiva, cada elemento do bloco de Jordan
associado cresce indefinidamente; se um autovalor tem parte real igual a zero e
algum bloco de Jordan de ordem 2 ou maior, então pelo menos um elemento
cresce indefinidamente
B Para ser assintoticamente estável, todo elemento tem que tender a zero quando
t → ∞, e assim, nenhum autovalor com parte real 0 ou positiva é permitido
c Reinaldo M. Palhares
°
pag.8
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna

0

Exemplo ẋ = 
 0
0
0
0
0
0


2
x.
Veja
que
∆(λ)
=
λ
(λ + 1)
0 

−1
B Lembre-se que o polinômio mı́nimo de A é definido como o polinômio mônico
ψ(λ) de menor grau tal que ψ(A) = 0...
B Note que A*(A+eye(3)) é uma matriz nula... Portanto o polinômio mı́nimo é
dado por ψ(λ) = λ(λ + 1) e portanto λ = 0 é uma raiz simples (multiplicidade
1) do polinômio mı́nimo. Os autovalores da matriz A são 0, 0 e −1 e a equação
é marginalmente estável...
c Reinaldo M. Palhares
°
pag.9
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna
Por outro lado, para o sistema

0

ẋ = 
 0
0
1
0
0
0


0 
x
−1
veja que A*(A+eye(3)) não é uma matriz nula. No entanto A^2*(A+eye(3)) é
um matriz nula, ie, ψ(λ) = λ2 (λ + 1) é o polinômio mı́nimo e λ = 0 não é
uma raiz simples do polinômio mı́nimo, portanto o sistema não é marginalmente
estável
c Reinaldo M. Palhares
°
pag.10
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna
B Como já discutido, todo pólo da matriz de transferência
G(s) = C(sI − A)−1 B + D
é também um autovalor de A. Assim, a estabilidade assintótica implica na BIBO
estabilidade
B Porém a BIBO estabilidade não implica, em geral, na estabilidade assintótica
B No geral o interesse é por sistemas que apresentem estabilidade assintótica ou
BIBO estabilidade (eventualmente com condições adicionais). Para osciladores
pode-se considerar questões associadas a estabilidade marginal
c Reinaldo M. Palhares
°
pag.11
Teoria de Sistemas Lineares – Aula 13
Estabilidade Interna de Sistemas Discretos
Para o sistema autônomo x(k + 1) = Ax(k), a solução para x(0) = x0 é
dada por x(k) = Ak x0
B O sistema é marginalmente estável ou estável no sentido de Lyapunov se toda
condição inicial finita x0 implicar em uma resposta limitada. É assintoticamente
estável se, além disso, a resposta tende a zero quando k → ∞
Teorema A equação x(k + 1) = Ax(k) é marginalmente estável se e somente
se todos os autovalores de A têm magnitudes menores ou iguais a 1 e aqueles que
tiverem magnitudes iguais a 1 forem raı́zes simples do polinômio mı́nimo de A
Teorema A equação x(k + 1) = Ax(k) é assintoticamente estável se e
somente se todos os autovalores de A têm magnitudes menores do que 1
B As transformações equivalentes não afetam a estabilidade do sistema, e as
formas de Jordan podem ser usadas no estudo da estabilidade. A estabilidade
assintótica implica em BIBO estabilidade mas o contrário não é verdadeiro
c Reinaldo M. Palhares
°
pag.12
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
Todos os autovalores de A têm parte real negativa se e somente se para qualquer
matriz simétrica definida positiva N (ie, N = N 0 > 0) a equação de Lyapunov
A0 M + M A = −N
tem uma única solução simétrica M e M é definida positiva (ie, M = M 0 > 0)
MATLAB relembrando: M=lyap(A,N). Um simples script:
A=rand(3), N=eye(3), M=lyap(A,N)
if all(real(eig(M)))>0
display(’M>0, Sistema estável’)
else display(’Sistema instável’)
end
c Reinaldo M. Palhares
°
pag.13
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
Corolário Todos os autovalores de uma matriz A n × n têm parte real negativa
se e somente se para qualquer matriz N̄ m × n com m < n tal que


N̄


 N̄ A 


rank 
= n (rank completo de colunas)

.


..


N̄ An−1
nm×n
a equação de Lyapunov A0 M + M A = −N̄ 0 N̄ , −N , tem uma única
solução simétrica M e M é definida positiva
B Para qualquer N̄ , a matriz N = N̄ 0 N̄ é semidefinida positiva...
B O teorema e seu corolário são válidos para qualquer escolha de N
c Reinaldo M. Palhares
°
pag.14
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
Demonstração
(−→) (Necessidade) A equação de Lyapunov é um caso
especial da equação de Sylvester. Como A e A0 têm os mesmos autovalores, se
A for assintoticamente estável (autovalores com parte real negativa), não existem
dois autovalores tais que
λi + λj = 0
e portanto a equação de Lyapunov é não singular e possui uma única solução M
(como concluimos do estudo da equação de Sylvester)
Define-se
M =
Z
∞
A0 t
e
N eAt dt
0
Substituindo na equação de Lyapunov...
c Reinaldo M. Palhares
°
pag.15
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
obtém-se:
0
A M + MA
=
Z
∞
0
∞
=
=
Z
0 A0 t
Ae
At
Ne
dt +
Z
∞
0
eA t N eAt Adt
0
d ³
0
´
eA t N eAt dt
dt
0
¯∞
¯
0
¯
eA t N eAt ¯
¯
t=0
=
0 − N = −N
pois eAt = 0 para t → ∞ se A tem autovalores com parte real negativa. Com
isso, prova-se que M dada acima é solução da equação. Veja que se N for
simétrica, M também é
c Reinaldo M. Palhares
°
pag.16
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
Como N é não singular, pode-se fatorâ-la na forma N = Ñ 0 Ñ com Ñ não
singular. Portanto,
0
x Mx =
Z
∞
0 A0 t
xe
0
At
Ñ Ñ e
0
xdt =
Z
∞
0
kÑ eAt xk22 dt
que é positiva para qualquer x 6= 0 (Ñ e eAt são não singulares), o que mostra
que M é definida positiva...
c Reinaldo M. Palhares
°
pag.17
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
(←−) (Suficiência) Agora, mostra-se que se N e M são definidas positivas,
então A é estável. Considere λ um autovalor de A associado ao autovetor v.
Então, Av = λv. Pré e pós multiplicando a equação de Lyapunov por v ∗ e v,
respectivamente, tem-se
−v ∗ N v
=
v ∗ A0 M v + v ∗ M Av
= (λ∗ + λ)v ∗ M v
= 2Re (λ)v ∗ M v
∗
∗
Como v N v e v M v são reais positivos
c Reinaldo M. Palhares
°
pag.18
=⇒ Re (λ) =
−v ∗ N v
2v ∗ M v
< 0...
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
Demonstração do Corolário (Necessidade) Segue os mesmos passos da prova
do teorema. Note que N̄ é uma matriz m × n, com m < n, e que portanto
N = N̄ 0 N̄ é semidefinida positiva. Ainda assim, M pode ser definida positiva
se o integrando N̄ eAt x não for identicamente nulo para todo t
# Por absurdo, suponha que N̄ eAt x ≡ 0 para todo t. Derivando em relação
ao tempo, tem-se N̄ AeAt x ≡ 0; fazendo a derivada n − 1 vezes:
2
6
6
6
6
6
6
4
N̄
N̄ A
..
.
N̄ An−1
3
7
7
7 At
7e x = 0
7
7
5
Como por hipótese o rank da matriz acima é n e eAt é não singular para todo t,
o único x solução seria x = 0. Assim, o integrando N̄ eAt x não pode ser
identicamente nulo para nenhum x 6= 0 e M é definida positiva
c Reinaldo M. Palhares
°
pag.19
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
(Suficiência) Considere agora Av = λv. Note que A 2 v = λAv =
An−1 v = λn−1 v. Assim,
2
3
2
2
3
N̄ v
N̄
N̄ v
7
6
6
6
7
6 N̄ A 7
6 N̄ Av
7
6 λN̄ v
7
6
6
6
7
7=6
6
7v = 6
..
..
..
6
6
6
7
7
7
6
6
6
7
.
.
.
5
4
4
4
5
N̄ An−1
N̄ An−1 v
λn−1 N̄ v
λ 2 v, . . . ,
3
7
7
7
7
7
7
5
Com a hipótese de rank completo de colunas, o vetor da esquerda é não nulo para v 6= 0
e portanto N̄ v (que compõe o vetor da direita) é um vetor não nulo. Como N̄ v 6= 0,
então de 2Re (λ)v ∗ M v = −v ∗ N̄ 0 N̄ v = −k N̄ vk22 , implica que Re (λ) < 0
B Na demonstração do teorema de Lyapunov e do colorário, usou-se a expressão:
R∞
0
M = 0 eA t N eAt dt. Esse resultado é estabelecido como teorema, e usado para
mostrar a unicidade da solução da equação de Lyapunov
c Reinaldo M. Palhares
°
pag.20
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
Teorema Se todos os autovalores de A têm parte real negativa, então a
equação de Lyapunov
A0 M + M A = −N
tem uma única solução para todo N dada por
Z ∞
0
eA t N eAt dt
M =
0
Demonstração de Unicidade Suponha que M1 e M2 são soluções. Então
A0 (M1 − M2 ) + (M1 − M2 )A = 0
m
0
eA t [A0 (M1 − M2 ) + (M1 − M2 )A] eAt =
Integrando de 0 a ∞...
c Reinaldo M. Palhares
°
pag.21
d h
dt
0
i
eA t (M1 − M2 )eAt = 0
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov
Integrando de 0 a ∞
h
¯∞
¯
i
0
¯
eA t (M1 − M2 )eAt ¯ = 0
¯
0
⇓
0 − (M1 − M2 ) = 0
⇓
M1 = M2 X
# Mesmo para A não estável, uma solução única existe se λi + λj 6= 0, mas
não da forma M acima. Se A for singular (pelo menos um autovalor nulo), a
equação de Lyapunov é singular e soluções podem ou não existir (dependendo se
N está ou não no range da equação)
c Reinaldo M. Palhares
°
pag.22
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov – Caso Discreto
Equação discreta
M − AM B = C
sendo A ∈ Rn×n , B ∈ Rm×m e C ∈ Rn×m . Como no caso contı́nuo, pode
ser expressa na forma (conjunto de equações lineares)
Ym=c
;
Y ∈ Rnm×nm , m, c ∈ Rnm×1
Seja ηk um autovalor de Y . Nesse caso,
ηk = 1 − λi µj
para i = 1, 2, . . . , n ; j = 1, 2, . . . , m
com λi e µj autovalores de A e B respectivamente
c Reinaldo M. Palhares
°
pag.23
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov – Caso Discreto
I Para verificar esse fato, defina S(M ) , M − AM B. A equação pode então
ser escrita S(M ) = C e um escalar η é um autovalor de S(M ) se
S(M ) = ηM . Considere u um autovetor à direita de A associado ao autovalor
λi e v um autovetor à esquerda de B associado ao autovalor µj
Au = λi u ;
vB = µj v
Assim, aplicando S a matrix n × m, uv, obtém-se
S(uv) = uv − AuvB = (1 − λi µj ) uv
|
{z
}
η
I Se não existir i e j tais que λi µj = 1, a equação é não singular e para cada
C a solução M é única
I Se λi µj = 1 para algum i e j, para C dado, a solução pode ou não existir
c Reinaldo M. Palhares
°
pag.24
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov – Caso Discreto
Teorema |λ(A)| < 1 se e somente se para qualquer N > 0 ou para
N = N̄ 0 N̄ , com N̄ uma matriz m × n com m < n, tal que


N̄


 N̄ A 


= n (rank completo de colunas)
rank 

..


.


N̄ An−1
nm×n
a equação discreta de Lyapunov
M − A0 M A = N
tem uma solução única M e M é definida positiva
c Reinaldo M. Palhares
°
pag.25
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov – Caso Discreto
Linhas gerais de uma demonstração (Necessidade) Para N > 0, se todos os
autovalores de A (iguais aos de A0 ) têm magnitude menor que 1, | λi λj | < 1
para todo i, j, a equação é não singular e uma única solução existe. Considere
M =
∞
X
(A0 )m N Am
m=0
Como | λi |< 1 para todo i, esta série infinita converge. Substituindo
!
à ∞
∞
X
X
0 m
m
0
(A0 )m N Am A =
(A ) N A − A
m=0
m=0
=
∞
X
(A0 )m N Am −
m=0
Ã
∞
X
m=0
(A0 )(m+1) N A(m+1)
!
define-se k = m + 1 e...
c Reinaldo M. Palhares
°
pag.26
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov – Caso Discreto
Re-ordenasse o somatório
∞
X
(A0 )m N Am −
m=0
= N+
Ã
(A0 )k N Ak
k=1
∞
X
(A0 )m N Am −
m=1
=N
∞
X
∞
X
!
=
(A0 )k N Ak
k=1
e se N for simétrica, M também é...
c Reinaldo M. Palhares
°
pag.27
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov – Caso Discreto
(Suficiência) Considere λ um autovalor de A associado ao autovetor v 6= 0
(Av = λv). Assim,
v∗ N v
=
v ∗ M v − v ∗ A0 M Av
=
v ∗ M v − λ∗ v ∗ M vλ
= (1− | λ |2 )v ∗ M v
Como os dois lados da equação são números reais e positivos, conclui-se que
(1− | λ |2 ) > 0 ou | λ |2 < 1. Isso estabelece o resultado para N > 0. O caso
N ≥ 0 pode ser mostrado de maneira similar
c Reinaldo M. Palhares
°
pag.28
Teoria de Sistemas Lineares – Aula 13
Teorema de Lyapunov – Caso Discreto
Teorema Se todos os autovalores de A têm magnitude menor do que 1, então
a equação discreta de Lyapunov
M − A0 M A = N
tem uma única solução para todo N dada por
M =
∞
X
(A0 )m N Am
m=0
B Se A tem um ou mais autovalores com magnitude maior do que 1, uma
solução única ainda existe se λi λj 6= 1 para todo i, j, mas não pode ser
computada pela série acima
c Reinaldo M. Palhares
°
pag.29
Teoria de Sistemas Lineares – Aula 13
Relação entre os Casos Contı́nuo e Discreto
B A condição de estabilidade do caso contı́nuo requer que todos os autovalores
estejam no semi-plano esquerdo aberto do plano complexo s. A correspondente
condição no caso discreto é que todos os autovalores estejam contidos no interior
do cı́rculo unitário do plano complexo z. Essas condições se relacionam pela
transformação bilinear
s=
z−1
;
z+1
z=
1+s
1−s
que define um mapeamento do semi-plano esquerdo aberto para o interior do
cı́rculo unitário e vice-versa
B Escrevendo as equações de Lyapunov (o subescrito d designa o caso discreto)
A0 M + M A = −N
c Reinaldo M. Palhares
°
pag.30
;
Md − A0d Md Ad = Nd
Teoria de Sistemas Lineares – Aula 13
Relação entre os Casos Contı́nuo e Discreto
Usando a transformação bilinear
A = (Ad + I)−1 (Ad − I)
;
Ad = (I + A)(I − A)−1
Substituindo Ad na Lyapunov discreta, obtém-se
¤
£
¤
£
−1
−1 0
= Nd
Md (I + A)(I − A)
Md − (I + A)(I − A)
multiplicando a esquerda por (I − A0 ) e a direita por (I − A) obtém-se:
(I − A0 ) Md (I − A) − (I + A0 )Md (I + A) = (I − A0 ) Nd (I − A)
A0 Md + Md A = −0.5(I − A0 )Nd (I − A)
que, comparada com a equação de Lyapunov do caso contı́nuo, fornece
A = (Ad + I)−1 (Ad − I) ; M = Md ; N = 0.5(I − A0 )Nd (I − A)
MATLAB dlyap (leia o “help”!)
c Reinaldo M. Palhares
°
pag.31
Teoria de Sistemas Lineares – Aula 13