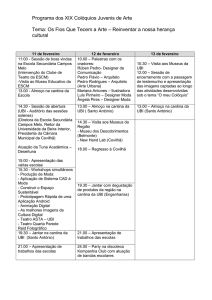
4 em 1 - Departamento de Matemática

Critérios de Avaliação
A avaliação ao longo das actividades lectivas será periódica, sendo efectuados
dois testes.
Os testes serão nos dias 22 de Novembro de 2010 e 10 de Janeiro de 2011.
Os dois testes serão cotados, cada um deles, para 10 valores.
Cálculo I
Designando por T1 a nota do primeiro teste e por T2 a nota do segundo teste,
a classificação final será calculada da seguinte forma:
1◦ Ciclo em Engenharia Electromecânica
1 Ciclo em Engenharia Electrotécnica e de Computadores
◦
– se T1 + T2 for inferior a 15,5 valores, a classificação final será o
arredondamento às unidades de T1 + T2 ;
António Bento
– se T1 + T2 for superior ou igual a 15,5 valores, terá de ser feita uma
prova oral; nessa prova oral será atribuída uma nota, que designaremos
por P O, entre 0 e 20 valores; a classificação final será o arredondamento
às unidades de
T1 + T2 + P O
max 15,
.
2
Departamento de Matemática
Universidade da Beira Interior
2010/2011
São aprovados os alunos com classificação final igual ou superior a 10 valores.
Todos os alunos são admitidos a exame.
António Bento (UBI)
Cálculo I
2010/2011
1 / 590
António Bento (UBI)
Cálculo I
2010/2011
3 / 590
Atendimento
Bibliografia
– Apostol, T.M., Cálculo, Vol. 1, Reverté, 1993
– Dias Agudo, F.R., Análise Real, Vol. I, Escolar Editora, 1989
O atendimento aos alunos será às quartas-feiras e às quintas-feiras, das 18
horas às 19 horas, no gabinete 4.25 do Departamento de Matemática.
– Demidovitch, B., Problemas e exercícios de Análise Matemática, McGrawHill,
1977
– Lima, E. L., Curso de Análise, Vol. 1, Projecto Euclides, IMPA, 1989
– Lima, E. L., Análise Real, Vol. 1, Colecção Matemática Universitária, IMPA, 2004
Caso este horário não seja conveniente, pode ser combinado outro horário com
o docente da cadeira através do email
– Mann, W. R., Taylor, A. E., Advanced Calculus, John Wiley and Sons, 1983
[email protected]
– Sarrico, C., Análise Matemática – Leituras e exercícios, Gradiva, 3a Ed., 1999
– Stewart, J., Calculus (International Metric Edition), Brooks/Cole Publishing
Company, 2008
– Swokowski, E. W., Cálculo com Geometria Analítica, Vol. 1 e 2, McGrawHill,
1983
António Bento (UBI)
Cálculo I
2010/2011
2 / 590
António Bento (UBI)
Cálculo I
2010/2011
4 / 590
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
Cálculo I
Índice
2010/2011
5 / 590
1
Funções reais de variável real: generalidades e exemplos
O conjunto dos números reais
Definição e exemplos de funções; função inversa; composição de funções
Função exponencial e função logarítmica
Funções trigonométricas e suas inversas
Funções hiperbólicas
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
Funções reais de variável real: generalidades e exemplos
O conjunto dos números reais
Definição e exemplos de funções; função inversa; composição de funções
Função exponencial e função logarítmica
Funções trigonométricas e suas inversas
Funções hiperbólicas
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
2010/2011
7 / 590
§1.1 O conjunto dos números reais
Índice
1
Cálculo I
No conjunto dos números reais, que representaremos por R, estão
definidas duas operações:
– uma adição, que a cada par de números reais (a, b) faz
corresponder um número a + b;
– uma multiplicação, que a cada par (a, b) associa um número
representado por a.b (ou a × b ou simplesmente ab).
Cálculo I
2010/2011
6 / 590
António Bento (UBI)
Cálculo I
2010/2011
8 / 590
§1.1 O conjunto dos números reais
§1.1 O conjunto dos números reais
Propriedades da adição
A1) Para cada a, b, c ∈ R,
a + (b + c) = (a + b) + c
(associatividade)
A2) Para cada a, b ∈ R,
a+b=b+a
(comutatividade)
A3) Existe um elemento 0 ∈ R, designado por "zero", tal que para cada
a∈R
a+0=0+a=a
(elemento neutro)
A4) Para cada a ∈ R, existe um elemento −a ∈ R tal que
a + (−a) = (−a) + a = 0
António Bento (UBI)
Cálculo I
Distributividade da multiplicação em relação à adição
D1) Para cada a, b, c ∈ R,
a(b + c) = (b + c)a = ab + ac
(simétrico)
2010/2011
9 / 590
António Bento (UBI)
§1.1 O conjunto dos números reais
M 1) Para cada a, b, c ∈ R,
a(bc) = (ab)c
(associatividade)
M 2) Para cada a, b ∈ R,
ab = ba
(comutatividade)
M 3) Existe um elemento 1 ∈ R, diferente de zero e designado por
"unidade", tal que para cada a ∈ R
a.1 = 1.a = a
(elemento neutro)
M 4) Para cada a ∈ R \ {0}, existe um elemento
aa−1 = a−1 a = 1
António Bento (UBI)
Cálculo I
Cálculo I
2010/2011
11 / 590
§1.1 O conjunto dos números reais
Propriedades da multiplicação
a−1
(distributividade)
∈ R tal que
(inverso)
2010/2011
10 / 590
Associadas a estas operações estão duas outras operações, a
subtracção e a divisão. A subtracção entre dois números reais a e b
representa-se por a − b e é definida por
a − b = a + (−b).
A divisão entre dois números reais a e b com b 6= 0 representa-se por
(ou a ÷ b ou a/b) e é definida por
a
b
a
= ab−1 .
b
A
a
, com b 6= 0, também se chama fracção entre a e b.
b
António Bento (UBI)
Cálculo I
2010/2011
12 / 590
§1.1 O conjunto dos números reais
§1.1 O conjunto dos números reais
Operações com fracções
Sejam a, b, c e d números reais tais que b 6= 0 e d 6= 0. Então
•
a c
ad + bc
+ =
;
b d
bd
•
a c
ad − bc
− =
;
b d
bd
•
a c
ac
= ;
b d
bd
Lei do anulamento do produto
Dados números reais a e b tem-se
ab = 0
se e só se
a=0
e/ou
b = 0.
a
a d
ad
• cb = × =
onde c 6= 0.
b
c
bc
d
António Bento (UBI)
Cálculo I
2010/2011
13 / 590
António Bento (UBI)
§1.1 O conjunto dos números reais
Cálculo I
2010/2011
15 / 590
2010/2011
16 / 590
§1.1 O conjunto dos números reais
Lei do corte da adição
Sejam a, b e c números reais. Então
a+c=b+c
Casos notáveis da multiplicação
Se a e b são números reais, então
se e só se
a = b.
i) (a + b)2 = a2 + 2ab + b2 ;
ii) (a − b)2 = a2 − 2ab + b2 ;
Lei do corte da multiplicação
iii) (a + b)(a − b) = a2 − b2 .
Sejam a, b e c números reais com c 6= 0. Então
ca = cb
se e só se
a = b.
António Bento (UBI)
Cálculo I
2010/2011
14 / 590
António Bento (UBI)
Cálculo I
§1.1 O conjunto dos números reais
§1.1 O conjunto dos números reais
Resolução de equações de primeiro grau
Quando a < b é uma proposição verdadeira, dizemos que a é menor
do que b.
Sejam a e b números reais. Então
i) a + x = b ⇔ x = b − a;
ii) ax = b ⇔ x =
Diz-se que a é menor ou igual do que b, e escreve-se
b
onde a 6= 0;
a
ou
a = b.
Dizemos que a é maior do que b, e escreve-se
a > b, se b < a.
Fórmula resolvente (de equações de segundo grau)
Obviamente, diz-se que a é maior ou igual do que b, e escreve-se
Sejam a, b e c números reais, com a 6= 0. Então
√
−b ± b2 − 4ac
2
ax + bx + c = 0 ⇔ x =
.
2a
António Bento (UBI)
se a < b
a 6 b,
Cálculo I
a > b, se b 6 a.
2010/2011
17 / 590
António Bento (UBI)
§1.1 O conjunto dos números reais
Cálculo I
2010/2011
19 / 590
§1.1 O conjunto dos números reais
Das quatro propriedades de ordem mencionadas atrás é possível
deduzir as seguintes propriedades:
Ordem
No conjunto dos números reais está definida uma relação de ordem,
relação essa que denotamos por < e que verifica, para quaisquer a, b,
c ∈ R, as seguintes propriedades:
O1) apenas uma das seguintes condições é verdadeira:
ou
a = b, ou
a < b, ou
Propriedades de ordem
Para quaisquer números reais a, b, c e d, tem-se
a) se a 6 b e b 6 a, então a = b;
b) se a 6= 0, então a2 > 0;
c) se a < b e c < d, então a + c < b + d;
b < a;
d) se a < b e c > 0, então ac < bc;
O2) se a < b e b < c, então a < c;
e) se a < b e c < 0, então ac > bc;
O3) se a < b, então a + c < b + c;
f ) se a > 0, então a−1 > 0;
g) se a < 0, então a−1 < 0;
a+b
< b;
h) se a < b, então a <
2
i) ab > 0 se e só se (a > 0 e b > 0) ou (a < 0 e b < 0).
O4) se 0 < a e 0 < b, então 0 < ab;
António Bento (UBI)
Cálculo I
2010/2011
18 / 590
António Bento (UBI)
Cálculo I
2010/2011
20 / 590
§1.1 O conjunto dos números reais
§1.1 O conjunto dos números reais
Representação geométrica dos intervalos
A relação de ordem permite-nos representar os números reais numa
recta ou num eixo.
−3
−2
−1
0
1
√ √
2 3 2
e
]a, b[
[a, b]
3π
[a, b[
]a, b]
António Bento (UBI)
Cálculo I
2010/2011
21 / 590
]a, +∞[
a
b
a
b
a
b
] − ∞, b[
b
a
b
] − ∞, b]
b
António Bento (UBI)
§1.1 O conjunto dos números reais
[a, +∞[
Cálculo I
a
a
2010/2011
23 / 590
§1.1 O conjunto dos números reais
As relações de ordem que definimos previamente permitem-nos definir
vários subconjuntos de R chamados intervalos. Dados dois números
reais tais que a 6 b, temos os seguintes conjuntos:
]a, b[ = {x ∈ R : a < x < b} ;
]a, b] = {x ∈ R : a < x 6 b} ;
[a, b] = {x ∈ R : a 6 x 6 b} ;
Inequações de segundo grau
Consideremos a inequação
ax2 + bx + c < 0,
a 6= 0.
2
a) Se a > 0 e b − 4ac > 0, então o conjunto solução da inequação é o
intervalo
]x1 , x2 [,
onde x1 e x2 são as soluções de ax2 + bx + c = 0 e x1 < x2 .
[a, b[ = {x ∈ R : a 6 x < b} ;
]a, +∞[ = {x ∈ R : a < x} ;
b) Se a > 0 e b2 − 4ac 6 0, então a inequação não tem soluções.
[a, +∞[ = {x ∈ R : a 6 x} ;
c) Se a < 0 e b2 − 4ac < 0, então o conjunto solução da inequação é R.
] − ∞, b[ = {x ∈ R : x < b} ;
d) Se a < 0 e b2 − 4ac > 0, então o conjunto solução da inequação é o
intervalo
] − ∞, x1 [ ∪ ]x2 , +∞[,
] − ∞, b] = {x ∈ R : x 6 b} ;
] − ∞, +∞[ = R
onde x1 e x2 são as soluções de ax2 + bx + c = 0 e x1 6 x2 .
António Bento (UBI)
Cálculo I
2010/2011
22 / 590
António Bento (UBI)
Cálculo I
2010/2011
24 / 590
§1.1 O conjunto dos números reais
§1.1 O conjunto dos números reais
Fazendo ∆ = b2 − 4ac, a figura seguinte ajuda-nos a resolver as
inequações de segundo grau.
Inequações de segundo grau (continuação)
Consideremos a inequação
ax2 + bx + c 6 0,
a 6= 0.
2
a) Se a > 0 e b − 4ac > 0, então o conjunto solução da inequação é o
intervalo
[x1 , x2 ],
a>0
∆>0
a>0
∆=0
a>0
∆<0
a<0
∆>0
a<0
∆=0
a<0
∆<0
António Bento (UBI)
Cálculo I
onde x1 e x2 são as soluções de ax2 + bx + c = 0 e x1 6 x2 .
b) Se a > 0 e b2 − 4ac < 0, então a inequação não tem soluções.
c) Se a < 0 e b2 − 4ac 6 0, então o conjunto solução da inequação é R.
d) Se a < 0 e b2 − 4ac > 0, então o conjunto solução da inequação é o
intervalo
] − ∞, x1 ] ∪ [x2 , +∞[,
onde x1 e x2 são as soluções de ax2 + bx + c = 0 e x1 < x2 .
António Bento (UBI)
Cálculo I
2010/2011
25 / 590
§1.1 O conjunto dos números reais
2010/2011
27 / 590
§1.1 O conjunto dos números reais
Intuitivamente, poderíamos construir os números naturais da
seguinte forma:
Para as inequações
ax2 + bx + c > 0,
1 é um número natural;
a 6= 0,
1 + 1 que representamos por 2 é um número natural;
1 + 1 + 1 = 2 + 1 = 3 é um número natural;
e
ax2 + bx + c > 0,
etc.
a 6= 0,
Assim,
temos algo semelhante aos dois casos anteriores.
António Bento (UBI)
Cálculo I
N = {1, 2, 3, 4, 5, . . .} .
2010/2011
26 / 590
António Bento (UBI)
Cálculo I
2010/2011
28 / 590
§1.1 O conjunto dos números reais
§1.1 O conjunto dos números reais
A partir dos números naturais podemos definir os números inteiros e os
números racionais.
Um número real diz-se um número inteiro se for um número natural,
ou se o seu simétrico for um número natural ou se for zero, isto é, o
conjunto dos números inteiros é o conjunto
Aos números reais que não são racionais chamamos de números
irracionais.
Os números
√ √
2, 3, π e e são números irracionais.
Z = N ∪ {0} ∪ {m ∈ R : −m ∈ N} .
Um número racional é um número real que pode ser representado
como o quociente entre dois números inteiros, isto é, o conjunto dos
números racionais é o conjunto
Q=
António Bento (UBI)
As inclusões seguintes são óbvias:
N ⊂ Z ⊂ Q ⊂ R.
m
: m ∈ Z, n ∈ Z \ {0} .
n
Cálculo I
2010/2011
29 / 590
António Bento (UBI)
§1.1 O conjunto dos números reais
Cálculo I
Por valor absoluto ou módulo de um elemento x ∈ R entende-se o
número real |x| definido por
|x| =
Assim, o número
0, 3333333...
(
se x > 0;
se x < 0.
x
−x
Uma forma equivalente de definir o módulo de um número real x é a
seguinte
|x| = max {x, −x} .
é um número racional, que também se representa por
0, 3(3)
Geometricamente, o módulo de um número dá-nos a distância desse
número à origem.
Além disso, este número também pode ser representado por
1
.
3
y
0
|y|
Cálculo I
31 / 590
§1.1 O conjunto dos números reais
Os números racionais também podem ser definidos através da
representação decimal. Um número real é racional se no sistema
decimal tiver uma dízima finita ou uma dízima infinita periódica.
António Bento (UBI)
2010/2011
2010/2011
30 / 590
António Bento (UBI)
x
|x|
Cálculo I
2010/2011
32 / 590
§1.1 O conjunto dos números reais
§1.1 O conjunto dos números reais
Propriedades do módulo (continuação)
Propriedades do módulo
Para quaisquer números reais a, b tem-se
a) |x| = a ⇔ x = a ∨ x = −a onde a > 0;
a) |a| = 0 se e só se a = 0;
b) |x| < a ⇔ x < a ∧ x > −a
b) |a| > 0;
c) |x| 6 a ⇔ x 6 a ∧ x > −a
c) |ab| = |a|.|b|;
d) |a + b| 6 |a| + |b|;
António Bento (UBI)
(desigualdade triangular)
d) |x| > a ⇔ x > a ∨ x < −a
e) |x| > a ⇔ x > a ∨ x 6 −a
Cálculo I
2010/2011
33 / 590
António Bento (UBI)
§1.1 O conjunto dos números reais
Cálculo I
2010/2011
35 / 590
§1.1 O conjunto dos números reais
A propriedade d) denomina-se desigualdade triangular pelo facto de
num triângulo o comprimento de qualquer lado ser menor do que a
soma dos comprimentos dos outros dois lados.
Podemos usar o módulo para calcular a distância entre dois números
reais. A distância entre dois números reais a e b é dada por
|a − b| .
Geometricamente,
a
|a − b|
|a + b| 6 |a| + |b|
António Bento (UBI)
Cálculo I
b
2010/2011
34 / 590
António Bento (UBI)
Cálculo I
2010/2011
36 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Índice
1
Funções reais de variável real: generalidades e exemplos
O conjunto dos números reais
Definição e exemplos de funções; função inversa; composição de funções
Função exponencial e função logarítmica
Funções trigonométricas e suas inversas
Funções hiperbólicas
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
A natureza da regra associada a f : A → B, e que nos permite
determinar o valor de f (x) quando é dado x ∈ A, é inteiramente
arbitrária, tendo apenas que verificar duas condições:
1) não pode haver excepções, isto é, para que o conjunto A seja o
domínio de f a regra deve de fornecer f (x) para todo o x ∈ A;
2) não pode haver ambiguidades, ou seja, a cada x ∈ A a regra deve
fazer corresponder um único f (x) ∈ B.
Cálculo I
2010/2011
37 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
António Bento (UBI)
Cálculo I
2010/2011
39 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Uma função f : A → B é definida à custa de três coisas:
• um conjunto A a que se chama domínio da função;
• um conjunto B chamado de conjunto de chegada da função;
• uma regra que a cada elemento de x ∈ A faz corresponder um e
um só elemento de B, elemento esse que se representa por f (x).
Referimo-nos a x ∈ A como um objecto e a f (x) ∈ B como a sua
imagem por f , respectivamente. Também usamos a expressão valor
de f em x para nos referirmos à imagem f (x).
As funções f que nós vamos estudar são funções reais de variável
real, ou seja, o domínio da função f é um subconjunto de R e o
conjunto de chegada é o conjunto dos números reais R. O domínio
costuma representar-se por D ou Df e usa-se a seguinte notação
f : D ⊆ R → R,
ou, de forma mais abreviada,
Ao conjunto das imagens chamamos contradomínio de f , ou seja, o
contradomínio é o conjunto
f : D → R.
f (A) = {f (x) ∈ B : x ∈ A} .
António Bento (UBI)
Cálculo I
2010/2011
38 / 590
António Bento (UBI)
Cálculo I
2010/2011
40 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo – Funções quadráticas
As funções definidas por
f (x) = ax2 + bx + c,
Exemplo – Primeira Lei de Ohm
A primeira lei de Ohm diz que a intensidade I da corrente eléctrica é
dada pelo quociente entre a diferença de potencial V e a resistência
eléctrica R do condutor:
V
I= .
R
Assim, num circuito eléctrico a intensidade da corrente pode ser vista
como uma função da diferença de potencial.
a 6= 0
designam-se por funções quadráticas. O seu domínio é o conjunto R
dos números reais e o contradomínio é o intervalo
"
"
#
#
b
b2
f −
, +∞ = c − , +∞
2a
4a
se a > 0 e é o intervalo
b
−∞, f −
2a
b2
= −∞, c −
4a
se a < 0.
António Bento (UBI)
Cálculo I
2010/2011
41 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
António Bento (UBI)
Cálculo I
2010/2011
43 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo – Funções afim
As funções dada por
f (x) = ax + b,
onde a e b são dois números reais fixos, designam-se por funções afim.
Quando b = 0, a expressão reduz-se a
e exprime que as variáveis entre x e y = f (x) existe proporcionalidade
directa, visto que o quociente dos dois valores correspondentes é
constante:
y
= a.
x
Dizemos então a função definida é linear. O domínio de uma função
afim é sempre o conjunto dos números reais. O contradomínio é o
conjunto R dos números reais, excepto no caso em que a = 0. Quando
a = 0 o contradomínio é o conjunto singular {b}.
Cálculo I
As funções funções f : R → R definidas por
f (x) = an xn + an−1 xn−1 + · · · + a1 x + a0 ,
f (x) = ax
António Bento (UBI)
Exemplo – Funções polinomiais
2010/2011
42 / 590
onde n ∈ N, a0 , a1 , . . . , an−1 ∈ R e an ∈ R \ {0} designam-se por
funções polinomiais.
Obviamente, as funções afim e as funções quadráticas são funções
polinomiais.
António Bento (UBI)
Cálculo I
2010/2011
44 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo
Exemplo – Funções racionais
As funções racionais são as funções definidas como o quociente entre
dois polinómios, ou seja, são as funções dadas por
f (x) =
xn
As funções afim f, g, h : R → R definidas por
f (x) = x,
g(x) = 2x + 1 e h(x) = −x − 1
tem os seguintes gráficos:
xn−1
+ · · · + a1 x + a0
an + an−1
,
bm xm + bm−1 xm−1 + · · · + b1 x + b0
g(x) = 2x + 1
f (x) = x
onde m, n ∈ N, a0 , a1 , . . . , an−1 , bm−1 , . . . , b1 , b0 ∈ R e an , bm ∈ R \ {0}.
h(x) = −x − 1
O seu domínio é o conjunto
1
−1
n
o
D = x ∈ R : bm xm + bm−1 xm−1 + · · · + b1 x + b0 6= 0 .
António Bento (UBI)
Cálculo I
2010/2011
1
−1
45 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
António Bento (UBI)
Cálculo I
2010/2011
47 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo
O gráfico de uma função quadrática é uma parábola. Por exemplo, a
função dada por
f (x) = x2 + x + 1
Dada uma função real de variável real f : D ⊆ R → R, o conjunto
tem o seguinte gráfico
G (f ) = {(a, f (a)) : a ∈ D}
f (x) = x2 + x + 1
designa-se por gráfico de f . Obviamente, este conjunto pode ser
representado no plano e a essa representação geométrica também se
chama gráfico.
1
−1
António Bento (UBI)
Cálculo I
2010/2011
46 / 590
António Bento (UBI)
1
Cálculo I
2010/2011
48 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo
Exemplo
Seja f : R → R a função definida por
As função dada por
f (x) = 1/x
f (x) = 2x + 3.
cujo domínio é R \ {0} tem o seguinte gráfico
Como
1
f (x) =
x
f (a) = f (b) ⇔ 2a + 3 = 2b + 3
⇔ 2a = 2b
1
−1
⇔ a = b,
1
a função f é injectiva. Além disso, dado b ∈ R, fazendo a =
temos
b−3
b−3
f (a) = f
+ 3 = b − 3 + 3 = b,
=2
2
2
−1
b−3
2
o que mostra que f é sobrejectiva.
António Bento (UBI)
Cálculo I
2010/2011
49 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Seja f : D ⊆ R → R uma função real de variável real. Dizemos que f é
injectiva se
para quaisquer a, b ∈ D tais que a 6= b se tem f (a) 6= f (b).
António Bento (UBI)
Cálculo I
2010/2011
51 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo
A função f : R → R definida por f (x) = x2 não é injectiva porque
A função f é sobrejectiva se
f (−1) = f (1).
para cada b ∈ R, existe a ∈ D tal que f (a) = b.
Obviamente, uma função real de variável real é sobrejectiva se o seu
contradomínio for o conjunto R dos números reais.
Além disso, também não é sobrejectiva porque o seu contradomínio é o
intervalo [0, +∞[.
As funções que são injectivas e sobrejectivas dizem-se bijectivas.
António Bento (UBI)
Cálculo I
2010/2011
50 / 590
António Bento (UBI)
Cálculo I
2010/2011
52 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Seja f : D ⊆ R → R uma função real de variável real injectiva. Recordemos
que o conjunto de todas as imagens por f de elementos de D, ou seja, o
conjunto
f (D) = {f (x) ∈ R : x ∈ D} ,
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo
Consideremos novamente a função f : R → R definida por
f (x) = 2x + 3.
se designa por contradomínio de f . Como f é injectiva, dado y ∈ f (D), existe
um e um só x ∈ D tal que
f (x) = y.
Já vimos que esta função é injectiva e, consequentemente, tem inversa. Além
disso, o contradomínio de f é R e, portanto,
Nestas condições podemos definir a inversa da função f que a cada y ∈ f (D)
faz corresponder x ∈ D tal que f (x) = y. Essa inversa representa-se por f −1 e
é a função
f −1 : f (D) → R
Como
f −1 : R → R.
y = f (x) ⇔ y = 2x + 3
⇔ −2x = −y + 3
⇔ 2x = y − 3
y 3
⇔ x= − ,
2 2
definida por
f
−1
(y) = x se e só se f (x) = y.
É evidente que para cada x ∈ D e para cada y ∈ f (D) se tem
f −1 (f (x)) = x
António Bento (UBI)
e
f −1 é definida por
f (f −1 (y)) = y.
Cálculo I
f −1 (y) =
2010/2011
53 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo
y
3
−
2 2
António Bento (UBI)
ou
f −1 (x) =
x 3
− .
2 2
Cálculo I
2010/2011
55 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo (continuação)
A função f : {1, 2, 3, 4} → R definida por
y=x
y = 2x + 3
f (1) = 9, f (2) = 8, f (3) = 7 e f (4) = 6
3
é injectiva e pode ser representada da seguinte forma:
f
2
4
b
b
6
3
b
b
7
2
b
b
8
1
b
b
9
f −1
1
y=
−4
−1
−1
1
2
3
−3
f −1 (6) = 4, f −1 (7) = 3, f −1 (8) = 2 e f −1 (9) = 1.
Cálculo I
−2
−2
e a sua inversa é a função f −1 : {6, 7, 8, 9} → R definida por
António Bento (UBI)
−3
x
3
−
2
2
2010/2011
−4
54 / 590
António Bento (UBI)
Cálculo I
2010/2011
56 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Exemplo
Seja f : R → R a função definida por
Sejam
f : Df ⊆ R → R
2
f (x) = x .
f (−1) = f (1) = 1.
Assim, a função f não tem inversa. No entanto, se pensarmos na restrição
desta função a [0, +∞[, ou seja, se usarmos a função g : [0, +∞[→ R definida
por g(x) = x2 , esta função já é injectiva pelo que podemos pensar na sua
√
inversa. Como o seu contradomínio é [0, +∞[ e y = x2 ⇒ x = y, a função
de domínio
Dg◦f = {x ∈ Df : f (x) ∈ Dg } ,
definida por
(g ◦ f )(x) = g(f (x)).
g −1 : [0, +∞[→ R
g −1 (x) =
António Bento (UBI)
√
x.
Cálculo I
2010/2011
57 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
y = x2
y=
2
2010/2011
59 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
f: R→R
√
−2
−1
−1
f (x) = x2 − 1
g : R \ {0} → R
e
g(x) =
1
.
x
Então g ◦ f tem por domínio o conjunto
1
2
Dg◦f = {x ∈ Df : f (x) ∈ Dg }
3
n
= x ∈ R : x2 − 1 ∈ R \ {0}
−2
e é definida por
−3
= R \ {−1, 1}
(g ◦ f )(x) = g(f (x)) = g(x2 − 1) =
−4
Cálculo I
e
as funções definidas por
x
1
António Bento (UBI)
Cálculo I
Sejam
y=x
3
−3
António Bento (UBI)
Exemplo
Exemplo (continuação)
−4
g : Dg ⊆ R → R
duas funções reais de variável real. A função composta de g com f
é a função
g ◦ f : Dg◦f ⊆ R → R,
Esta função não é injectiva porque, por exemplo,
é definida por
e
2010/2011
58 / 590
António Bento (UBI)
Cálculo I
o
x2
1
.
−1
2010/2011
60 / 590
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Índice
1
Funções reais de variável real: generalidades e exemplos
O conjunto dos números reais
Definição e exemplos de funções; função inversa; composição de funções
Função exponencial e função logarítmica
Funções trigonométricas e suas inversas
Funções hiperbólicas
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Exemplo (continuação)
Se em vez de g ◦ f calcularmos f ◦ g temos
Df ◦g = {x ∈ Dg : g(x) ∈ Df }
1
= x ∈ R \ {0} : ∈ R
x
= R \ {0}
e
(f ◦ g)(x) = f (g(x)) = f (1/x) =
António Bento (UBI)
1
− 1.
x2
Cálculo I
2010/2011
61 / 590
António Bento (UBI)
§1.2 Definição e exemplos de funções; função inversa; composição de funções
Cálculo I
2010/2011
63 / 590
§1.3 Função exponencial e função logarítmica
Exemplo (continuação)
y=
3
x2
Dado um número real positivo a > 0, pretendemos estudar a função
1
−1
f :R→R
definida por
2
f (x) = ax ,
1
que se designa por função exponencial de base a.
−3
−2
−1
−1
−2
1
2
3
Repare-se que quando a = 1 temos a função constante
1
y = 2 −1
x
f (x) = 1x = 1.
−3
António Bento (UBI)
Cálculo I
2010/2011
62 / 590
António Bento (UBI)
Cálculo I
2010/2011
64 / 590
§1.3 Função exponencial e função logarítmica
§1.3 Função exponencial e função logarítmica
Propriedades da função exponencial
y
Sejam x, y ∈ R e a, b ∈ ]0, +∞[. Então
y = 4x
a) a0 = 1
y = 3x
y = ex
y = 2x
b) ax+y = ax ay
1
ax
ax
d) ax−y = y
a
x y
e) (a ) = axy
c) a−x =
1
f ) ax bx = (ab)x
x
g) se x > y e a > 1, então ax > ay
h) se x > y e 0 < a < 1, então ax < ay
Gráfico de funções exponenciais
i) se a ∈ ]0, +∞[ \ {1} a função exponencial é injectiva
j) se a ∈ ]0, +∞[ \ {1} o contradomínio da função exponencial é ]0, +∞[
António Bento (UBI)
Cálculo I
2010/2011
65 / 590
§1.3 Função exponencial e função logarítmica
António Bento (UBI)
Cálculo I
y=
y=
a>1
1 x
2
1 x
3
y=
1 x
4
y
1
a=1
x
x
Gráfico da função exponencial
António Bento (UBI)
67 / 590
§1.3 Função exponencial e função logarítmica
y
0<a<1
2010/2011
Cálculo I
Gráfico de funções exponenciais
2010/2011
66 / 590
António Bento (UBI)
Cálculo I
2010/2011
68 / 590
§1.3 Função exponencial e função logarítmica
§1.3 Função exponencial e função logarítmica
y
Quando a ∈]0, 1[ ∪ ]1, +∞[, a função exponencial ax é injectiva e, por
conseguinte, tem inversa. Essa inversa chama-se logaritmo na base a
e representa-se por loga .
a>1
Assim, tendo em conta que o contradomínio da função exponencial é o
intervalo ]0, +∞[, temos que
x
loga : ]0, +∞[→ R
1
é a função definida por
loga x = y se e só se x = ay .
0<a<1
Obviamente, quando a = e temos a função logaritmo natural que
representamos por ln.
António Bento (UBI)
Cálculo I
2010/2011
69 / 590
§1.3 Função exponencial e função logarítmica
Gráfico da função logaritmo de base a
António Bento (UBI)
Cálculo I
2010/2011
71 / 590
§1.3 Função exponencial e função logarítmica
Propriedades da função logarítmica
y
Sejam x, y ∈ R+ e a, b ∈ ]0, +∞[\ {1}. Então
log2 x
a) loga (xy) = loga x + loga y
ln x
1
= − loga x
x
x
c) loga = loga x − loga y
y
b) loga
log4 x
x
1
d) loga (x ) = α loga x
α
e) loga x = logb x loga b
log1/4 x
log1/3 x
f ) loga 1 = 0
g) se x > y e a > 1, então loga x > loga y
log1/2 x
h) se x > y e 0 < a < 1, então loga x < loga y
i) a função logarítmica é injectiva;
Gráfico de funções logarítmicas
j) o contradomínio da função logarítmica é R
António Bento (UBI)
Cálculo I
2010/2011
70 / 590
António Bento (UBI)
Cálculo I
2010/2011
72 / 590
§1.4 Funções trigonométricas e suas inversas
Índice
1
2
Funções reais de variável real: generalidades e exemplos
O conjunto dos números reais
Definição e exemplos de funções; função inversa; composição de funções
Função exponencial e função logarítmica
Funções trigonométricas e suas inversas
Funções hiperbólicas
1
cos α
sen α
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
α em radianos
α
Cálculo I
2010/2011
73 / 590
§1.4 Funções trigonométricas e suas inversas
António Bento (UBI)
1
Cálculo I
2010/2011
75 / 590
§1.4 Funções trigonométricas e suas inversas
D
BE
CD
=
AE
AD
E
As funções seno e coseno, cujo domínio é o conjunto dos números
reais, fazem corresponder a cada x ∈ R
AB
AC
=
AE
AD
α
A
B
• seno:
sen α =
• coseno:
cos α =
António Bento (UBI)
C
sen x
e
cos x,
respectivamente. O contradomínio destas duas funções é o intervalo
[−1, 1].
comprimento do cateto oposto
BE
CD
=
=
comprimento da hipotenusa
AE
AD
comprimento do cateto adjacente
AB
AC
=
=
comprimento da hipotenusa
AE
AD
Cálculo I
2010/2011
74 / 590
António Bento (UBI)
Cálculo I
2010/2011
76 / 590
§1.4 Funções trigonométricas e suas inversas
§1.4 Funções trigonométricas e suas inversas
y
1
−2π
−π
− 3π
2
−π
2
π
2
π
x
3π
2
2π
−1
Outra função trigonométrica importante é a função tangente, definida
pela fórmula
sen x
,
tg x =
cos x
que está definida para todos os pontos x tais que cos x 6= 0, ou seja, o
domínio da função tangente é o conjunto
Gráfico da função seno
x ∈ R : x 6=
π
+ kπ, k ∈ Z .
2
O seu contradomínio é o conjunto dos números reais.
António Bento (UBI)
Cálculo I
2010/2011
77 / 590
António Bento (UBI)
§1.4 Funções trigonométricas e suas inversas
Cálculo I
2010/2011
79 / 590
§1.4 Funções trigonométricas e suas inversas
y
y
1
−2π
− 3π
2
−π
π
2
−π
2
π
x
3π
2
2π
−2π
−1
− 3π
2
−π
π
2
−π
2
π
x
3π
2
2π
Gráfico da função coseno
Gráfico da função tangente
António Bento (UBI)
Cálculo I
2010/2011
78 / 590
António Bento (UBI)
Cálculo I
2010/2011
80 / 590
§1.4 Funções trigonométricas e suas inversas
§1.4 Funções trigonométricas e suas inversas
cos x
= cotg x
1 sen x
A função cotangente é dada pela expressão
cotg x =
cos x
.
sen x
sen x
= tg x
cos x
x
O seu domínio é o conjunto
1
{x ∈ R : x 6= kπ, k ∈ Z}
e o contradomínio é o conjunto dos números reais.
António Bento (UBI)
Cálculo I
2010/2011
81 / 590
§1.4 Funções trigonométricas e suas inversas
António Bento (UBI)
Cálculo I
2010/2011
83 / 590
2010/2011
84 / 590
§1.4 Funções trigonométricas e suas inversas
y
A função secante é definida por
sec x =
1
,
cos x
o seu domínio é o conjunto
−π
−2π
− 3π
2
2π
π
−π
2
π
2
x
x ∈ R : x 6=
3π
2
π
+ kπ, k ∈ Z
2
e o seu contradomínio é o conjunto
] − ∞, −1] ∪ [1, +∞[.
Gráfico da função cotangente
António Bento (UBI)
Cálculo I
2010/2011
82 / 590
António Bento (UBI)
Cálculo I
§1.4 Funções trigonométricas e suas inversas
§1.4 Funções trigonométricas e suas inversas
y
y
1
1
−2π
− 3π
2
−π
2
−π
π
2
−1
π
x
3π
2
2π
−π
−2π − 3π
2
Gráfico da função secante
António Bento (UBI)
Cálculo I
−π
2
−1
π
π
2
2π
3π
2
x
Gráfico da função cosecante
2010/2011
85 / 590
António Bento (UBI)
§1.4 Funções trigonométricas e suas inversas
Cálculo I
2010/2011
87 / 590
§1.4 Funções trigonométricas e suas inversas
A função cosecante é definida por
cosec x =
1
,
sen x
0
o seu domínio é o conjunto
{x ∈ R : x 6= kπ, k ∈ R}
seno
0
coseno
1
tangente
0
e o seu contradomínio é o conjunto
] − ∞, −1] ∪ [1, +∞[.
António Bento (UBI)
Cálculo I
2010/2011
86 / 590
António Bento (UBI)
π
6
1
2
√
3
2
√
3
3
π
4
√
2
2
√
2
2
1
π
3
√
3
2
1
2
√
3
Cálculo I
π
2
π
3π
2
1
0
-1
0
-1
0
n.d.
0
n.d.
2010/2011
88 / 590
§1.4 Funções trigonométricas e suas inversas
§1.4 Funções trigonométricas e suas inversas
Reduções ao primeiro quadrante (continuação)
Fórmula fundamental da trigonometria
sen2 x + cos2 x = 1
sen(3π/2 − x) = − cos x
cos(3π/2 − x) = − sen x
Desta fórmula resultam imediatamente as seguintes fórmulas
1 + tg2 x =
1
cos2 x
e
1 + cotg2 x =
sen(3π/2 + x) = − cos x
1
,
sen2 x
cos(3π/2 + x) = sen x
António Bento (UBI)
e
xx
cos(2π − x) = cos x
sen(2π + x) = sen x
1 + cotg2 x = cosec2 x.
Cálculo I
cos(2π + x) = cos x
2010/2011
89 / 590
§1.4 Funções trigonométricas e suas inversas
António Bento (UBI)
Cálculo I
2010/2011
91 / 590
2010/2011
92 / 590
§1.4 Funções trigonométricas e suas inversas
Reduções ao primeiro quadrante
Reduções ao primeiro quadrante (continuação)
tg(−x) = − tg(x)
sen(−x) = − sen x
cos(−x) = cos x
cotg(−x) = − cotg(x)
1
tg(π/2 − x) = cotg x
sen(π/2 − x) = cos x
cos(π/2 − x) = sen x
cotg(π/2 − x) = tg x
xx
sen(π/2 + x) = cos x
x
x
cos(π/2 + x) = − sen x
tg(π/2 + x) = − cotg x
1
x
x
cotg(π/2 + x) = − tg x
sen(π − x) = sen x
tg(π − x) = − tg x
sen(π + x) = − sen x
tg(π + x) = tg x
cos(π − x) = − cos x
cotg(π − x) = − cotg x
cos(π + x) = − cos x
cotg(π + x) = cotg x
António Bento (UBI)
1
x
x
sen(2π − x) = − sen x
que podem ser reescritas da seguinte forma
1 + tg2 x = sec2 x
1
Cálculo I
2010/2011
90 / 590
António Bento (UBI)
Cálculo I
§1.4 Funções trigonométricas e suas inversas
§1.4 Funções trigonométricas e suas inversas
A função seno não é injectiva pelo que não tem inversa.
No entanto,
π π
considerando a restrição da função seno ao intervalo − , , a que se
2 2
chama restrição principal, ou seja, considerando a função
π π
f: − ,
→ R,
2 2
Resolução de equações trigonométricas
sen x = sen α ⇔ x = α + 2kπ ∨ x = π − α + 2kπ, k ∈ Z
definida por
cos x = cos α ⇔ x = α + 2kπ ∨ x = −α + 2kπ, k ∈ Z
f (x) = sen x,
tg x = tg α ⇔ x = α + kπ, k ∈ Z
tem-se que a função f é injectiva. À inversa desta função chama-se
arco seno e representa-se por arc sen. Assim,
cotg x = cotg α ⇔ x = α + kπ, k ∈ Z
arc sen : [−1, 1] → R
e é definida da seguinte forma
π π
arc sen x = y se e só se x = sen y e y ∈ − ,
.
2 2
António Bento (UBI)
Cálculo I
2010/2011
93 / 590
§1.4 Funções trigonométricas e suas inversas
António Bento (UBI)
sen(x + y) = sen x cos y + sen y cos x
sen(x − y) = sen x cos y − sen y cos x
cos(x + y) = cos x cos y − sen x sen y
cos(x − y) = cos x cos y + sen x sen y
sen(2x) = 2 sen x cos x
cos(2x) = cos2 x − sen2 x = 2 cos2 x − 1 = 1 − 2 sen2 x
x−y
x+y
cos
2
2
x+y
x−y
sen x − sen y = 2 sen
cos
2
2
x+y
x−y
cos x − cos y = −2 sen
sen
2
2
x−y
x+y
cos
cos x + cos y = 2 cos
2
2
sen x + sen y = 2 sen
Cálculo I
2010/2011
95 / 590
2010/2011
96 / 590
§1.4 Funções trigonométricas e suas inversas
Fórmulas trigonométricas
António Bento (UBI)
Cálculo I
2010/2011
94 / 590
António Bento (UBI)
x
arc sen x
0
0
1
π/2
−1
−π/2
1/2
π/6
−1/2
√
2/2
√
− 2/2
√
3/2
√
− 3/2
−π/6
π/4
−π/4
π/3
−π/3
Cálculo I
§1.4 Funções trigonométricas e suas inversas
§1.4 Funções trigonométricas e suas inversas
y
π
2
x
arc cosx
0
π/2
1
0
−1
π
1/2
π/3
−1/2
√
2/2
√
− 2/2
√
3/2
√
− 3/2
2π/3
b
−1
x
1
b
− π2
Gráfico da função arco seno
António Bento (UBI)
Cálculo I
2010/2011
97 / 590
§1.4 Funções trigonométricas e suas inversas
António Bento (UBI)
π/4
3π/4
π/6
5π/6
Cálculo I
2010/2011
99 / 590
§1.4 Funções trigonométricas e suas inversas
y
Considerando a restrição da função coseno ao intervalo [0, π], ou seja, a
função
g : [0, π] → [−1, 1]
b
π
definida por
g(x) = cos x,
π
2
tem-se que g é uma função injectiva. A inversa desta função
representa-se por arc cos e chama-se arco coseno. Assim,
arc cos : [−1, 1] → R
é a função definida por
b
arc cosx = y se e só se x = cos y e y ∈ [0, π] .
x
1
−1
Gráfico da função arco coseno
António Bento (UBI)
Cálculo I
2010/2011
98 / 590
António Bento (UBI)
Cálculo I
2010/2011
100 / 590
§1.4 Funções trigonométricas e suas inversas
Seja
§1.4 Funções trigonométricas e suas inversas
π π
h: − ,
→R
2 2
a função definida por
y
π
2
h(x) = tg x.
A função h é injectiva, pelo que h tem inversa. A inversa desta função
representa-se por arc tg e chama-se arco tangente. Assim
x
arc tg : R → R
− π2
é a função definida por
Gráfico da função arco tangente
π π
arc tg x = y se e só se x = tg y e y ∈ − ,
.
2 2
António Bento (UBI)
Cálculo I
2010/2011
101 / 590
§1.4 Funções trigonométricas e suas inversas
x
arc tg x
0
0
1
−1
√
3
3
√
3
−
3
√
3
√
− 3
António Bento (UBI)
Cálculo I
2010/2011
103 / 590
§1.4 Funções trigonométricas e suas inversas
À inversa da restrição ao intervalo ]0, π[ da função cotangente
chamamos arco cotangente e representamos essa função por arc cotg.
Assim,
arc cotg : R → R
π
4
π
−
4
é a função definida por
π
6
arc cotg x = y se e só se x = cotg y e y ∈ ]0, π[ .
π
−
6
π
3
π
−
3
Cálculo I
António Bento (UBI)
2010/2011
102 / 590
António Bento (UBI)
Cálculo I
2010/2011
104 / 590
§1.4 Funções trigonométricas e suas inversas
arc cotg x
x
π
2
π
4
3π
4
0
1
−1
√
3
3
√
3
−
3
√
3
π
3
2π
3
π
6
5π
6
√
− 3
António Bento (UBI)
Índice
Cálculo I
2010/2011
105 / 590
1
Funções reais de variável real: generalidades e exemplos
O conjunto dos números reais
Definição e exemplos de funções; função inversa; composição de funções
Função exponencial e função logarítmica
Funções trigonométricas e suas inversas
Funções hiperbólicas
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
§1.4 Funções trigonométricas e suas inversas
Cálculo I
2010/2011
107 / 590
§1.5 Funções hiperbólicas
y
π
As funções
definidas por
π
2
senh : R → R
e
cosh : R → R
ex − e−x
2
e
cosh x =
senh x =
x
ex + e−x
2
designam-se por seno hiperbólico e por coseno hiperbólico,
respectivamente.
Gráfico da função arco cotangente
António Bento (UBI)
Cálculo I
2010/2011
106 / 590
António Bento (UBI)
Cálculo I
2010/2011
108 / 590
§1.5 Funções hiperbólicas
§1.5 Funções hiperbólicas
y
y = cosh x
ex − e−x
=y
2
⇔ ex − e−x = 2y
senh x = y ⇔
1
⇔ ex − e−x −2y = 0
x
⇔ e2x −2y ex −1 = 0
x
⇔e =
2y +
⇔ ex = y +
X
XX2y
2+
4y 2 + 4
−
4y
4
X
XXX
∨ ex
=X
X
X
2
2
p
q
p
y2 + 1
q
⇔ x = ln y +
y2
+1
y = senh x
Gráfico das funções seno e coseno hiperbólico
Logo o contradomínio do seno hiperbólico é R.
António Bento (UBI)
Cálculo I
2010/2011
109 / 590
António Bento (UBI)
§1.5 Funções hiperbólicas
Cálculo I
ex + e−x
=y
2
⇔ ex + e−x = 2y
Associada a estas funções está a função tangente hiperbólica. A
tangente hiperbólica é a função
⇔ ex + e−x −2y = 0
tgh : R → R
⇔ e2x −2y ex +1 = 0
⇔e =
2y +
⇔ ex = y +
⇔ x = ln(y +
definida por
4y 2 − 4
2y − 4y 2 − 4
∨ ex =
2
2
p
q
y 2 − 1 ∨ ex = y −
q
y2
111 / 590
§1.5 Funções hiperbólicas
cosh x = y ⇔
x
2010/2011
p
q
tgh x =
y2 − 1
− 1) ∨ x = ln y −
q
y2
senh x
ex − e−x
e2x −1
= x
=
.
cosh x
e + e−x
e2x +1
−1
Assim, o contradomínio do coseno hiperbólico é o intervalo [1, +∞[.
António Bento (UBI)
Cálculo I
2010/2011
110 / 590
António Bento (UBI)
Cálculo I
2010/2011
112 / 590
§1.5 Funções hiperbólicas
tgh x = y ⇔
§1.5 Funções hiperbólicas
e2x −1
=y
e2x +1
É fácil mostrar que as seguintes igualdades são válidas:
⇔ e2x −1 = y e2x +y
a) cosh2 x − senh2 x = 1
1
b) 1 − tgh2 x =
cosh2 x
c) senh(x + y) = senh x cosh y + senh y cosh x
⇔ (1 − y) e2x = y + 1
y+1
1−y
1
y+1
⇔ x = ln
2
1−y
⇔ e2x =
d) cosh(x + y) = cosh x cosh y + senh x senh y
y+1
> 0, o que é equivalente a −1 < y < 1. Logo
1−y
o contradomínio da tangente hiperbólica é o intervalo ] − 1, 1[.
Assim, temos de ter
António Bento (UBI)
Cálculo I
2010/2011
113 / 590
António Bento (UBI)
§1.5 Funções hiperbólicas
Cálculo I
2010/2011
115 / 590
2010/2011
116 / 590
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
y
1
x
−1
Gráfico da função tangente hiperbólica
António Bento (UBI)
Cálculo I
2010/2011
114 / 590
António Bento (UBI)
Cálculo I
§2.1 Breves noções de topologia em R
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
-1
0
1/2
1
2
Seja A o conjunto ]0, 1]. Então
1
é um ponto interior a A,
2
2 é um ponto exterior a A,
−1 é um ponto exterior a A,
0 é um ponto fronteiro a A e
1 é um ponto fronteiro a A.
António Bento (UBI)
Cálculo I
2010/2011
117 / 590
António Bento (UBI)
§2.1 Breves noções de topologia em R
Cálculo I
2010/2011
119 / 590
§2.1 Breves noções de topologia em R
Seja A um subconjunto de R. Um ponto a ∈ R diz-se interior a A
se existir ε > 0 tal que ]a − ε, a + ε[ ⊆ A.
O ponto a diz-se exterior a A
O conjunto dos pontos interiores a A designa-se por interior de A e
representa-se por
int A ou A◦ ,
o conjunto dos pontos exteriores a A chama-se exterior de A e
representa-se por
ext A
se existir ε > 0 tal que ]a − ε, a + ε[ ∩ A = ∅
(ou seja, ]a − ε, a + ε[ ⊆ R \ A).
Um ponto diz-se fronteiro a A se não for interior, nem exterior, isto é,
a é um ponto fronteiro de A
e o conjunto dos pontos fronteiros a A diz-se a fronteira de A e
representa-se por
fr A.
se para cada ε > 0, ]a − ε, a + ε[ ∩ A 6= ∅ e ]a − ε, a + ε[ ∩ (R \ A) 6= ∅.
António Bento (UBI)
Cálculo I
2010/2011
118 / 590
António Bento (UBI)
Cálculo I
2010/2011
120 / 590
§2.1 Breves noções de topologia em R
§2.1 Breves noções de topologia em R
Exemplos
Um ponto a ∈ R diz-se aderente a um subconjunto A ⊆ R
a) Para o intervalo A =]0, 1] temos
int A =]0, 1[,
se para cada ε > 0, ]a − ε, a + ε[ ∩ A 6= ∅.
ext A =] − ∞, 0[ ∪ ]1, +∞[ e fr A = {0, 1} .
O conjuntos dos pontos aderentes de um conjunto A designa-se por
aderência ou fecho de A e representa-se por
b) Considerando o intervalo I =]a, b[, com a < b, verifica-se
imediatamente que
int I =]a, b[,
A.
Das definições resulta que
ext I =] − ∞, a[ ∪ ]b, +∞[ e fr I = {a, b} .
A = int A ∪ fr A
c) Os intervalos ]a, b], [a, b[ e [a, b], onde a < b, têm o mesmo interior,
o mesmo exterior e a mesma fronteira que o intervalo ]a, b[.
e
int A ⊆ A ⊆ A.
d) int R = R, ext R = ∅, fr R = ∅.
e) int ∅ = ∅, ext ∅ = R, fr ∅ = ∅.
António Bento (UBI)
Cálculo I
2010/2011
121 / 590
António Bento (UBI)
§2.1 Breves noções de topologia em R
Cálculo I
2010/2011
123 / 590
§2.1 Breves noções de topologia em R
Exemplos
a) Se A =]0, 1[, então A = [0, 1].
b) Dado I = [a, b], com a < b, temos
a) Da definição resulta imediatamente que int A, ext A e fr A são
conjuntos disjuntos dois a dois e que
I = [a, b].
R = int A ∪ ext A ∪ fr A.
c) Os intervalos ]a, b[, [a, b[ e ]a, b], onde a < b, têm a mesma aderência
que o intervalo [a, b].
b) Outra consequência imediata da definição é o seguinte
ext A = int (R \ A)
e
d) Seja A = [1, 2[ ∪ {3, 4}. Então
fr A = fr (R \ A) .
A = [1, 2] ∪ {3, 4} .
e) Obviamente, R = R e ∅ = ∅.
António Bento (UBI)
Cálculo I
2010/2011
122 / 590
António Bento (UBI)
Cálculo I
2010/2011
124 / 590
§2.1 Breves noções de topologia em R
§2.1 Breves noções de topologia em R
Sejam A um subconjunto de R e a um número real. Diz-se que a é um
ponto de acumulação de A
Um subconjunto A de R diz-se aberto se
se para cada ε > 0, ]a − ε, a + ε[ ∩ (A \ {a}) 6= ∅.
A = int A
O conjunto dos pontos de acumulação de um conjunto A representa-se
por
A′
e diz-se fechado se
A = A.
e designa-se por derivado. Os pontos de A que não são pontos de
acumulação de A designam-se por pontos isolados.
António Bento (UBI)
Cálculo I
2010/2011
125 / 590
António Bento (UBI)
§2.1 Breves noções de topologia em R
2010/2011
127 / 590
§2.1 Breves noções de topologia em R
Exemplos
Exemplos
a) O derivado do intervalo I = [a, b[, com a < b, é o conjunto
I ′ = [a, b].
a) Como
int ]0, 1[=]0, 1[,
b) Os intervalos ]a, b[, ]a, b] e [a, b], onde a < b, têm o mesmo derivado
que o intervalo [a, b[.
c) Seja A =]0, 2] ∪ {3}. Então
temos que ]0, 1[ é um conjunto aberto. Por outro lado,
]0, 1[ = [0, 1]
e, por conseguinte, ]0, 1[ não é fechado.
int A =]0, 2[,
b) O intervalo [0, 1] é um conjunto fechado porque
ext A =] − ∞, 0[ ∪ ]2, 3[ ∪ ]3, +∞[,
[0, 1] = [0, 1]
fr A = {0, 2, 3},
e não é um conjunto aberto porque
A = [0, 2] ∪ {3} e
int [0, 1] =]0, 1[.
A′ = [0, 2].
d) R′ = R e ∅′ = ∅.
António Bento (UBI)
Cálculo I
c) Os conjuntos ∅ e R são simultaneamente abertos e fechados.
Cálculo I
2010/2011
126 / 590
António Bento (UBI)
Cálculo I
2010/2011
128 / 590
§2.2 Limites: definição, propriedades e exemplos
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
3
Tendo em conta que
0 < |x − a| < δ ⇔ x ∈ ]a − δ, a + δ[\ {a}
e que
tem-se o seguinte
Cálculo diferencial em R
|f (x) − b| < ε ⇔ f (x) ∈ ]b − ε, b + ε[,
lim f (x) = b
x→a
⇔ ∀ε > 0 ∃δ > 0 ∀x ∈ D (x ∈ ]a − δ, a + δ[ \ {a} ⇒ f (x) ∈ ]b − ε, b + ε[) .
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
Cálculo I
2010/2011
129 / 590
§2.2 Limites: definição, propriedades e exemplos
António Bento (UBI)
Cálculo I
2010/2011
131 / 590
§2.2 Limites: definição, propriedades e exemplos
Sejam D um subconjunto de R, f : D → R uma função, a um ponto de
acumulação de D e b ∈ R. Diz-se que b é o limite (de f ) quando x
tende para a, e escreve-se
y
f (a)
b
b+ε
lim f (x) = b,
x→a
b+ε
se para cada ε > 0, existe δ > 0 tal que
b
b−ε
|f (x) − b| < ε para qualquer x ∈ D tal que 0 < |x − a| < δ.
b−ε
Simbolicamente, tem-se o seguinte
a+δa+δa+δ
a−δa−δa−δ
a−δaa+δ
lim f (x) = b ⇔ ∀ε > 0 ∃δ > 0 ∀x ∈ D (0 < |x − a| < δ ⇒ |f (x) − b| < ε)
x
x→a
Interpretação geométrica do conceito de limite de uma função
António Bento (UBI)
Cálculo I
2010/2011
130 / 590
António Bento (UBI)
Cálculo I
2010/2011
132 / 590
§2.2 Limites: definição, propriedades e exemplos
§2.2 Limites: definição, propriedades e exemplos
Propriedades dos limites
Sejam D ⊆ R, f, g : D → R e a um ponto de acumulação de D. Suponhamos
que existem lim f (x) e lim g(x). Então
x→a
x→a
a) existe lim [f (x) + g(x)] e
Sejam f : Df ⊆ R → R, g : Dg ⊆ R → R duas funções reais de variável
real. Suponhamos que a ∈ R é um ponto de acumulação de Df e que
b ∈ Dg é um ponto de acumulação de Dg . Se
x→a
lim [f (x) + g(x)] = lim f (x) + lim g(x);
x→a
x→a
Propriedades dos limites (continuação)
x→a
b) existe lim [f (x)g(x)] e
lim f (x) = b e
x→a
x→a
h
i h
i
lim [f (x)g(x)] = lim f (x) . lim g(x) ;
x→a
x→a
então
x→a
lim (g ◦ f )(x) = lim g(f (x)) = g(b).
f (x)
e
x→a g(x)
x→a
c) se lim g(x) 6= 0, existe lim
x→a
lim g(x) = g(b),
x→b
x→a
lim f (x)
f (x)
= x→a
.
x→a g(x)
lim g(x)
lim
x→a
António Bento (UBI)
Cálculo I
2010/2011
133 / 590
António Bento (UBI)
§2.2 Limites: definição, propriedades e exemplos
Cálculo I
2010/2011
135 / 590
§2.2 Limites: definição, propriedades e exemplos
Um dos limites mais conhecidos é o seguinte
ex −1
= 1.
x→0
x
Propriedades dos limites (continuação)
Sejam D ⊆ R, f, g : D ⊆ R → R e a um ponto de acumulação de D.
Suponhamos que
lim f (x) = 0
x→a
e que g é uma função limitada em D ∩ ]a − δ, a + δ[ para algum δ > 0,
isto é, existe c > 0 tal que
lim
ln(1 + x)
. Fazendo a
x→0
x
mudança de variável ln(1 + x) = y, tem-se x = ey −1 e quando x → 0
A partir deste limite podemos calcular lim
tem-se y → 0. Assim,
|g(x)| 6 c para qualquer x ∈ ]a − δ, a + δ[ ∩ D.
lim
x→0
Então
lim [f (x).g(x)] = 0.
ln(1 + x)
y
= lim y
= lim
y→0 e −1
y→0
x
1
ey −1
y
=
1
= 1.
1
Logo
x→a
ln(1 + x)
= 1.
x→0
x
lim
António Bento (UBI)
Cálculo I
2010/2011
134 / 590
António Bento (UBI)
Cálculo I
2010/2011
136 / 590
§2.2 Limites: definição, propriedades e exemplos
§2.2 Limites: definição, propriedades e exemplos
Provemos que
Outro limite bastante importante é o seguinte:
sen x
= 1.
x→0 x
lim
lim
x→0
arc sen x
=1
x
e
lim
x→0
arc tg x
=1.
x
No primeiro limite fazemos a mudança de variável arc sen x = y e
obtemos
Usando este limite podemos calcular vários outros limites. Por
exemplo,
arc sen x
y
1
1
= lim
= lim sen y = = 1.
x→0
y→0 sen y
y→0
x
1
y
lim
sen x
tg x
1 sen x
1
lim
= lim cos x = lim
= 1 = 1.
x→0 x
x→0 x
x→0 cos x
x
1
Para o segundo limite fazemos a mudança de variável y = arc tg x e vem
Portanto
tg x
= 1.
x→0 x
arc tg x
y
1
1
= lim
= lim tg y = = 1.
x→0
y→0 tg y
y→0
x
1
y
lim
António Bento (UBI)
Cálculo I
lim
2010/2011
137 / 590
António Bento (UBI)
§2.2 Limites: definição, propriedades e exemplos
Cálculo I
2010/2011
139 / 590
2010/2011
140 / 590
Índice
Vejamos que
lim
x→0
1 − cos x
1
= .
x2
2
De facto,
lim
x→0
António Bento (UBI)
1 − cos x
(1 − cos x)(1 + cos x)
= lim
x→0
x2
x2 (1 + cos x)
1 − cos2 x
1
= lim
2
x→0
x
(1 + cos x)
2
sen x
1
= lim
x→0 x2
(1 + cos x)
2
sen x
1
= lim
x→0
x
(1 + cos x)
1
1
= 12 = .
2
2
Cálculo I
2010/2011
138 / 590
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
Cálculo I
§2.3 Limites infinitos e limites no infinito
§2.3 Limites infinitos e limites no infinito
Sejam D um subconjunto de R, f : D → R uma função e a um ponto
de acumulação de D. Diz-se que
Sejam D um subconjunto de R não majorado e f : D → R uma função.
Diz-se que
f tende para +∞ quando x tende para +∞,
f tende para +∞ quando x tende para a,
e escreve-se
e escreve-se
lim f (x) = +∞,
lim f (x) = +∞,
x→+∞
x→a
se para cada L > 0, existe M > 0 tal que
se para cada L > 0, existe δ > 0 tal que
f (x) > L para qualquer x ∈ D tal que x > M .
f (x) > L para qualquer x ∈ D tal que 0 < |x − a| < δ.
Formalmente,
Simbolicamente,
lim f (x) = +∞ ⇔ ∀L > 0 ∃δ > 0 ∀x ∈ D (0 < |x − a| < δ ⇒ f (x) > L) .
x→a
António Bento (UBI)
Cálculo I
2010/2011
lim f (x) = +∞ ⇔ ∀L > 0 ∃M > 0 ∀x ∈ D (x > M ⇒ f (x) > L) .
x→+∞
141 / 590
António Bento (UBI)
§2.3 Limites infinitos e limites no infinito
Cálculo I
2010/2011
143 / 590
§2.3 Limites infinitos e limites no infinito
Sejam D um subconjunto de R não majorado, f : D → R uma função e
b ∈ R. Dizemos que
f tende para b quando x tende para +∞,
A partir dos três limites anteriores podemos definir os restantes casos.
Assim,
• lim f (x) = −∞ se lim −f (x) = +∞
x→a
e escreve-se
lim f (x) = b,
x→+∞
se para cada ε > 0, existe M > 0 tal que
|f (x) − b| < ε para qualquer x ∈ D tal que x > M .
Simbolicamente,
x→a
lim f (x) = b se lim f (−x) = b
•
x→−∞
•
x→+∞
•
x→−∞
•
x→−∞
x→+∞
lim f (x) = −∞ se lim −f (x) = +∞
x→+∞
lim f (x) = +∞ se lim f (−x) = +∞
x→+∞
lim f (x) = −∞ se lim −f (−x) = +∞
x→+∞
lim f (x) = b ⇔ ∀ε > 0 ∃M > 0 ∀x ∈ D (x > M ⇒ |f (x) − b| < ε) .
x→+∞
António Bento (UBI)
Cálculo I
2010/2011
142 / 590
António Bento (UBI)
Cálculo I
2010/2011
144 / 590
§2.3 Limites infinitos e limites no infinito
§2.3 Limites infinitos e limites no infinito
Nos limites infinitos podemos usar a regra do limite da soma desde que
se adoptem as convenções
(+∞) + a = +∞ = a + (+∞)
(−∞) + a = −∞ = a + (−∞)
(+∞) + (+∞) = +∞
(−∞) + (−∞) = −∞
onde a é um número real qualquer.
A regra do limite do quociente mantém-se se se adoptarem as seguintes
convenções
a
a
=
= 0, a ∈ R
+∞
−∞
a
= +∞, a > 0
0+
a
= −∞, a < 0
0+
a
= −∞, a > 0
0−
a
= +∞, a < 0
0−
onde 0+ significa que
f (x) → 0 e f (x) > 0 na intersecção do domínio com um intervalo aberto que
contém o ponto em que estamos a calcular o limite
e 0− significa que
f (x) → 0 e f (x) < 0 na intersecção do domínio com um intervalo aberto que
contém o ponto em que estamos a calcular o limite.
António Bento (UBI)
Cálculo I
2010/2011
145 / 590
§2.3 Limites infinitos e limites no infinito
António Bento (UBI)
(+∞) × a = +∞ = a × (+∞) onde a ∈
R+
147 / 590
2010/2011
148 / 590
Não se faz nenhuma convenção para os símbolos
(+∞) × a = −∞ = a × (+∞) onde a ∈
R−
(+∞) + (−∞),
(−∞) × a = −∞ = a × (−∞) onde a ∈ R+
0 × (+∞),
+∞
,
+∞
(−∞) × a = +∞ = a × (−∞) onde a ∈ R−
(+∞) × (+∞) = +∞ = (−∞) × (−∞)
+∞
,
−∞
0 × (−∞),
−∞
,
+∞
−∞
−∞
0
0
pois são símbolos de indeterminação.
(+∞) × (−∞) = −∞ = (−∞) × (+∞)
Cálculo I
2010/2011
§2.3 Limites infinitos e limites no infinito
Adoptando as convenções que se seguem, podemos usar a regra do
limite do produto:
António Bento (UBI)
Cálculo I
2010/2011
146 / 590
António Bento (UBI)
Cálculo I
§2.3 Limites infinitos e limites no infinito
§2.3 Limites infinitos e limites no infinito
Vejamos
Exemplos
lim
a) É óbvio que
x→+∞
lim x = +∞
e
lim x = −∞.
lim ln
x→−∞
x→+∞
1
b) Seja f : R \ {0} → R a função definida por f (x) = . Então
x
Cálculo I
lim
x→+∞
2010/2011
149 / 590
ln 1 +
= lim
x→+∞
1/x
1
x
1
1+
x
x = lim
y→0
ln (1 + y)
= 1.
y
1
1+
x
x
ln[(1+ x1 )
= lim e
x
x→+∞
António Bento (UBI)
x
lim ln[(1+ x1 ) ]
] = ex→+∞
= e1 = e .
Cálculo I
2010/2011
151 / 590
2010/2011
152 / 590
Outros limites importantes são os seguintes
c) Seja f : R → R definida por

x−1


 2x + 1
se x > 0,
lim ax =
x→+∞
2


 −2x + 3
se x < 0.
3x2 + 8
e
1
1−
x−1
x
= lim
lim f (x) = lim
= lim
1
x→+∞
x→+∞ 2x + 1
x→+∞
x→+∞
x 2+
2+
x
x 1−
−2x + 3
lim f (x) = lim
= lim
x→−∞
x→−∞ 3x2 + 8
x→−∞
António Bento (UBI)
1
= lim x ln 1 +
x→+∞
x
§2.3 Limites infinitos e limites no infinito
Exemplos (continuação)
2
x Assim,
§2.3 Limites infinitos e limites no infinito
e
1
1+
x
lim ln
1
1
=
= 0.
x→−∞ x
−∞
Então
x→+∞
= lim
f (x) =
=e.
e que fazendo a mudança de variável y = 1/x temos
1
1
=
=0
lim
x→+∞ x
+∞
António Bento (UBI)
x
Comecemos por observar que
x→+∞
e
1
1+
x
lim ax =
1
x = 1
1
2
x
x→−∞
Destes limites resulta que
3
3
−2 + 2
2
2
x
x
= lim
=− .
8
8
x→−∞
3
x2 3 + 2
3+ 2
x
x
x2 −2 +
Cálculo I
2010/2011
150 / 590

+∞
0

0
António Bento (UBI)
se 0 < a < 1
se a > 1
+∞
lim ln x = +∞
x→+∞
se a > 1
e
Cálculo I
se 0 < a < 1
.
lim ln x = −∞ .
x→0
§2.4 Limites laterais
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
É evidente que se existe
lim f (x),
x→a
então também existe
lim f (x)
x→a
x∈A
para qualquer subconjunto A de D do qual a é ponto de acumulação de
Ae
lim f (x) = lim f (x).
x→a
x→a
x∈A
Assim, se existirem dois limites relativos distintos, o limite não existe.
Cálculo I
2010/2011
153 / 590
António Bento (UBI)
§2.4 Limites laterais
Cálculo I
2010/2011
155 / 590
2010/2011
156 / 590
§2.4 Limites laterais
Exemplo
Sejam A um subconjunto de D ⊆ R, a um ponto de acumulação de A e
Consideremos a função f : R → R definida por
f (x) =
f : D → R.
Chama-se limite de f no ponto a relativo a A (ou limite quando
x tende para a no conjunto A) ao limite em a (quando exista) da
restrição de f a A e usa-se a notação
(
1
0
se x ∈ Q,
se x ∈ R \ Q.
Então
lim f (x) = 1
x→a
x∈Q
e
lim f (x).
lim f (x) = 0
x→a
x∈A
x→a
x∈R\Q
qualquer que seja a ∈ R. Logo não existe
lim f (x).
x→a
António Bento (UBI)
Cálculo I
2010/2011
154 / 590
António Bento (UBI)
Cálculo I
§2.4 Limites laterais
§2.4 Limites laterais
Observações
Seja f : D ⊆ R → R e consideremos os conjuntos
a) É óbvio que lim f (x) = b é equivalente a
Da+ = {x ∈ D : x > a} = D∩ ]a, +∞[
x→a
x∈A
e
Da−
∀ε > 0 ∃δ > 0 ∀x ∈ A (0 < |x − a| < δ ⇒ |f (x) − b| < ε) .
= {x ∈ D : x < a} = D∩ ] − ∞, a[.
b) Como
Definem-se, respectivamente, os limites laterais à direita e à
esquerda da seguinte forma
é equivalente a
x∈D
lim f (x) = lim f (x)
∀ε > 0 ∃δ > 0 ∀x ∈ D (−δ < x − a < 0 ⇒ |f (x) − b| < ε) .
lim f (x) = lim f (x),
Analogamente, lim+ f (x) = b é equivalente a
x→a
x∈Da−
x→a
desde que a seja ponto de acumulação de Da+ e de Da− , respectivamente.
António Bento (UBI)
Cálculo I
−δ <x−a<0
x→a−
e
x→a−
e
0 < |x − a| < δ
e, portanto, lim f (x) = b é equivalente a
x→a
x∈Da+
x→a+
e
x ∈ Da−
2010/2011
157 / 590
∀ε > 0 ∃δ > 0 ∀x ∈ D (0 < x − a < δ ⇒ |f (x) − b| < ε) .
António Bento (UBI)
§2.4 Limites laterais
Cálculo I
2010/2011
159 / 590
§2.4 Limites laterais
Exemplo
Seja f : R → R a função dada por
f (x) =
(
1
0
Também existem limites laterais para limites infinitos:
se x > 0,
se x < 0.
lim f (x) = +∞
x→a−
⇔ ∀L > 0 ∃δ > 0 ∀x ∈ D (−δ < x − a < 0 ⇒ f (x) > L)
caso a seja um ponto da acumulação de Da− e
Esta função é conhecida por função de Heaviside. É óbvio que
lim
x→0
x∈]0,+∞[
lim f (x) = +∞
f (x) = lim f (x) = 1
x→a+
x→0+
⇔ ∀L > 0 ∃δ > 0 ∀x ∈ D (0 < x − a < δ ⇒ f (x) > L)
quando a é um ponto de acumulação de Da+ .
e
lim
x→0
x∈]−∞,0[
António Bento (UBI)
f (x) = lim f (x) = 0.
x→0−
Cálculo I
2010/2011
158 / 590
António Bento (UBI)
Cálculo I
2010/2011
160 / 590
§2.4 Limites laterais
§2.4 Limites laterais
Exemplos
a) É evidente que
Usando os limites anteriores podemos definir os seguintes limites:
b) Também se tem
x→a+
lim
1
1
1
= + 2 = + = +∞
2
x
(0 )
0
lim−
1
1
1
= − 2 = + = +∞.
2
x
(0 )
0
x→0+
e
x→0
Cálculo I
1
1
= − = −∞.
x
0
x→0−
x→a−
António Bento (UBI)
lim
e que
• lim f (x) = −∞ se lim −f (x) = +∞.
x→a+
1
1
= + = +∞
x
0
x→0+
• lim f (x) = −∞ se lim −f (x) = +∞;
x→a−
lim
2010/2011
161 / 590
António Bento (UBI)
Cálculo I
§2.4 Limites laterais
2010/2011
163 / 590
§2.4 Limites laterais
Vejamos que
lim tg x = +∞ e
Propriedade dos limites laterais
x→ π2 −
Sejam D ⊆ R, f : D → R e a um ponto de acumulação de Da+ e Da− .
Então
lim f (x) = b,
De facto,
onde b ∈ R ou b = +∞ ou b = −∞, se e só se existem e são iguais a b
os limites laterais, ou seja,
e
1
sen x
= + = +∞
cos x
0
lim tg x = lim
1
sen x
= − = −∞.
cos x
0
x→ π2 +
lim f (x) = lim f (x) = b.
x→a−
lim− tg x = lim−
x→ π
2
x→a
x→ π2
+
x→ π
2
De forma análoga temos
x→a+
lim tg x = −∞ e
x→− π2 +
António Bento (UBI)
Cálculo I
lim tg x = −∞ .
+
x→ π
2
2010/2011
162 / 590
António Bento (UBI)
lim tg x = +∞ .
−
x→− π
2
Cálculo I
2010/2011
164 / 590
§2.4 Limites laterais
§2.5 Assímptotas
y = f (x)
De
lim tg x = +∞
−
x→ π
2
e
lim tg x = −∞
+
x→− π
2
conclui-se imediatamente que
d
lim arc tg x =
x→+∞
π
2
e
lim arc tg x = −
x→−∞
y = mx + b
π
.
2
d = f (x) − (mx + b)
lim [f (x) − (mx + b)] = 0
x→+∞
António Bento (UBI)
Cálculo I
2010/2011
165 / 590
António Bento (UBI)
Cálculo I
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
167 / 590
§2.5 Assímptotas
Índice
1
2010/2011
Sejam D um subconjunto não majorado e f : D → R uma função. A
recta de equação y = mx + b diz-se uma assímptota não vertical à
direita do gráfico de f se
lim [f (x) − (mx + b)] = 0.
x→+∞
Se D é um subconjunto não minorado e f : D → R é uma função,
diz-se que a recta de equação y = mx + b é uma assímptota não
vertical à esquerda do gráfico de f se
lim [f (x) − (mx + b)] = 0.
x→−∞
Cálculo I
2010/2011
166 / 590
António Bento (UBI)
Cálculo I
2010/2011
168 / 590
§2.5 Assímptotas
§2.5 Assímptotas
Assímptotas não verticais à direita
Sejam D um subconjunto de R não majorado e f : D → R uma função.
Para que o gráfico de f tenha uma assímptota não vertical à direita é
necessário e suficiente que existam e sejam finitos os limites
f (x)
a) lim
x→+∞ x
(que designaremos por m),
b)
lim [f (x) − mx].
x→+∞
Verificadas estas condições, e designando por b o segundo limite,
assímptota à direita do gráfico de f tem a equação
Cálculo I
m = lim
x→+∞
f (x)
x
e
b = lim [f (x) − mx]
x→+∞
e se estes limites existirem e forem finitos, a assímptota é a recta de
equação y = mx + b. Para as assímptotas não verticais à esquerda
temos de calcular os limites
f (x)
x→−∞ x
m = lim
y = mx + b.
António Bento (UBI)
Assim, para calcularmos uma assímptota não vertical à direita temos
de calcular os seguintes limites
e
b = lim [f (x) − mx]
x→−∞
e caso existam e sejam finitos ambos os limites, a assímptota é a recta
de equação y = mx + b.
2010/2011
169 / 590
António Bento (UBI)
§2.5 Assímptotas
Cálculo I
2010/2011
171 / 590
§2.5 Assímptotas
Assímptotas não verticais à esquerda
Sejam D um subconjunto de R não minorado e f : D → R uma função.
Para que o gráfico de f tenha uma assímptota não vertical à esquerda é
necessário e suficiente que existam e sejam finitos os limites
f (x)
a) lim
x→−∞ x
(que designaremos por m),
b)
lim [f (x) − mx].
Diz-se que a recta de equação x = a é uma assímptota vertical ao
gráfico de f se pelo menos umas das seguintes condições se verificar:
lim f (x) = +∞,
lim f (x) = +∞
x→−∞
x→a−
Verificadas estas condições, e designando por b o segundo limite,
assímptota à esquerda do gráfico de f tem a equação
lim f (x) = −∞,
x→a+
x→a+
ou
lim f (x) = −∞.
x→a−
y = mx + b.
António Bento (UBI)
Cálculo I
2010/2011
170 / 590
António Bento (UBI)
Cálculo I
2010/2011
172 / 590
§2.5 Assímptotas
§2.6 Funções contínuas: definição, propriedades e exemplos
y = f (x)
Sejam D um subconjunto de R, f : D → R uma função e a ∈ D. Diz-se
que f é contínua no ponto a se para cada ε > 0, existir δ > 0 tal que
|f (x) − f (a)| < ε para qualquer x ∈ D tal que |x − a| < δ.
Simbolicamente,
f é contínua em a
a
⇔ ∀ε > 0 ∃δ > 0 ∀x ∈ D (|x − a| < δ ⇒ |f (x) − f (a)| < ε) .
Dizemos que a ∈ D é um ponto de descontinuidade de f se f não é
contínua em a.
Uma função f : D → R é contínua se for contínua em todos os pontos
de D.
A recta de equação x = a é uma assímptota vertical ao gráfico de f
António Bento (UBI)
Cálculo I
2010/2011
173 / 590
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
Cálculo I
2010/2011
175 / 590
§2.6 Funções contínuas: definição, propriedades e exemplos
Índice
1
António Bento (UBI)
y
f (a)+ε
f (a)+ε
f (a)
f (a)−ε
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
f (a)−ε
a+δa+δa+δ
a−δa−δa−δ
a−δaa+δ
António Bento (UBI)
x
Interpretação geométrica do conceito de função contínua num ponto
Cálculo I
2010/2011
174 / 590
António Bento (UBI)
Cálculo I
2010/2011
176 / 590
§2.6 Funções contínuas: definição, propriedades e exemplos
§2.6 Funções contínuas: definição, propriedades e exemplos
Observações
Exemplos
a) Ao contrário do que acontece na definição de limite, só faz sentido
considerar pontos do domínio D quando estamos a investigar a
continuidade de uma função.
b) Se a é um ponto isolado de D, então a função f : D → R é contínua
em a. De facto, dado ε > 0, basta escolher δ > 0 tal que
Assim, a condição x ∈ D ∧ |x − a| < δ é equivalente a x = a e, por
conseguinte,
|f (x) − f (a)| = 0 < ε.
c) Se a ∈ D é um ponto de acumulação de D, então f : D → R é
contínua em a se e só se
c) As funções polinomiais, ou seja, as funções f : R → R definidas por
x→a
2010/2011
onde n ∈ N e a0 , a1 , . . . , an−1 , an ∈ R, são funções contínuas.
d) As funções racionais, ou seja, as funções dadas por
f (x) =
an xn + an−1 xn−1 + · · · + a1 x + a0
,
bm xm + bm−1 xm−1 + · · · + b1 x + b0
onde m, n ∈ N, a0 , a1 , . . . , an−1 , b0 , b1 , . . . , bm−1 ∈ R e an , bm ∈ R \ {0},
são funções contínuas.
lim f (x) = f (a).
Cálculo I
b) A função f : R → R definida por f (x) = x é contínua. Esta função
designa-se por identidade.
f (x) = an xn + an−1 xn−1 + · · · + a1 x + a0 ,
]a − δ, a + δ[ ∩ D = {a} .
António Bento (UBI)
a) As funções constante são contínuas.
177 / 590
§2.6 Funções contínuas: definição, propriedades e exemplos
António Bento (UBI)
Cálculo I
179 / 590
§2.6 Funções contínuas: definição, propriedades e exemplos
Propriedades da continuidade
Exemplos (continuação)
a) Sejam f, g : D ⊆ R → R duas funções contínuas em a ∈ D. Então
e) A função f : R → R dada por f (x) = |x| é contínua.
√
f ) A função f : [0, +∞[→ R dada por f (x) = x é contínua.
f + g, f − g e f g são contínuas em a
e se g(a) 6= 0 então
2010/2011
g) As funções exponencial e logarítmica são funções contínuas.
h) As funções trigonométricas são funções contínuas.
f
é contínua em a.
g
i) As inversas das funções trigonométricas são funções contínuas.
j) As funções hiperbólicas são funções contínuas.
b) Sejam f : Df ⊆ R → R e g : Dg ⊆ R → R duas funções. Se f é
contínua em a ∈ Df e g é contínua em f (a) ∈ Dg , então
k) A função definida por
2
ln(x − 2)
f (x) = sen ex −x +
arc tg(x − 5)
g ◦ f é contínua em a.
António Bento (UBI)
Cálculo I
é uma função contínua pois é a composição de funções contínuas.
2010/2011
178 / 590
António Bento (UBI)
Cálculo I
2010/2011
180 / 590
§2.6 Funções contínuas: definição, propriedades e exemplos
§2.6 Funções contínuas: definição, propriedades e exemplos
Exemplos (continuação)
Obviamente, se a é um ponto de acumulação de D ∩ ]a, +∞[, então
k) A função f : R → R definida por
f (x) =
(
1
0
se x > 0
se x < 0
f é contínua à direita em a ⇔ lim f (x) = f (a)
x→a+
e caso a seja um ponto de acumulação de D ∩ ] − ∞, a[ temos
não é contínua em x = 0 porque não existe lim f (x). Obviamente, a
x→0
função é contínua em para qualquer x ∈ R \ {0}.
l) Seja f : R → R a função definida por
( sen x
f (x) =
0
x
f é contínua à esquerda em a ⇔ lim f (x) = f (a).
x→a−
se x 6= 0
Propriedade
se x = 0
Sejam f : D ⊆ R → R e a ∈ D. Então f é contínua em a se e só se é
contínua à esquerda e à direita em a.
Então f não é contínua em x = 0 porque
sen x
= 1 6= f (0) = 0.
lim f (x) = lim
x→0
x→0
x
É claro que a função é contínua em para qualquer x ∈ R \ {0}.
António Bento (UBI)
Cálculo I
2010/2011
181 / 590
António Bento (UBI)
§2.6 Funções contínuas: definição, propriedades e exemplos
a restrição de f a D ∩ [a, +∞[ é contínua em a.
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
Breves noções de topologia em R
Limites: definição, propriedades e exemplos
Limites infinitos e limites no infinito
Limites laterais
Assímptotas
Funções contínuas: definição, propriedades e exemplos
Propriedades fundamentais das funções contínuas
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
A função diz-se contínua em a à esquerda se
a restrição de f a D ∩ ] − ∞, a] é contínua em a.
Assim, f é contínua à direita em a se e só se
∀ε > 0 ∃δ > 0 ∀x ∈ D (0 6 x − a < δ ⇒ |f (x) − f (a)| < ε) ,
e é contínua à esquerda em a se e só se
∀ε > 0 ∃δ > 0 ∀x ∈ D (−δ < x − a 6 0 ⇒ |f (x) − f (a)| < ε) .
Cálculo I
2010/2011
2010/2011
183 / 590
2010/2011
184 / 590
Índice
Sejam f : D → R e a ∈ D. Diz-se que a função f é contínua em a à
direita se
António Bento (UBI)
Cálculo I
182 / 590
António Bento (UBI)
Cálculo I
§2.7 Propriedades fundamentais das funções contínuas
§2.7 Propriedades fundamentais das funções contínuas
Corolário dos valores intermédios ou de Bolzano
Teorema de Bolzano ou dos valores intermédios
Sejam a e b números reais tais que a < b e seja
Sejam a e b números reais tais que a < b e
f : [a, b] → R
f : [a, b] → R
uma função contínua tal que
uma função contínua tal que
f (a).f (b) < 0.
f (a) 6= f (b).
Então existe
Então para qualquer valor k entre f (a) e f (b), existe um ponto
c ∈ [a, b] tal que
f (c) = k.
António Bento (UBI)
Cálculo I
2010/2011
c ∈]a, b[
tal que
f (c) = 0.
185 / 590
§2.7 Propriedades fundamentais das funções contínuas
António Bento (UBI)
Cálculo I
2010/2011
§2.7 Propriedades fundamentais das funções contínuas
y
y
f (b)
f (b)
a
b
b
f (a)
a
c
b
Cálculo I
b
c1
c2
b
b
c3 b
x
b
x
Interpretação geométrica do Corolário do Teorema de Bolzano
Interpretação geométrica do Teorema de Bolzano
António Bento (UBI)
b
b
k
f (a)
187 / 590
2010/2011
186 / 590
António Bento (UBI)
Cálculo I
2010/2011
188 / 590
§2.7 Propriedades fundamentais das funções contínuas
§2.7 Propriedades fundamentais das funções contínuas
Seja f : D ⊆ R → R uma função definida num subconjunto não vazio
D.
Exemplos
Provemos que a função f : [0, 1] → R definida por
f (x) = cos
πx
2
Dizemos que f tem um máximo (absoluto) no ponto a ∈ D ou que
f (a) é um máximo (absoluto) de f se
− x2
f (x) 6 f (a) para todo o x ∈ D.
tem (pelo menos) um zero em [0, 1]. Obviamente, esta função é
contínua pois é a composição de funções contínuas. Como
f (0)f (1) = cos (0) − 02
cos
π
2
− 12
Quando
f (x) > f (a) para todo o x ∈ D,
= 1(−1) = −1,
pelo (Corolário do) Teorema de Bolzano, f tem de ter pelo menos um
zero no intervalo ]0, 1[.
António Bento (UBI)
Cálculo I
2010/2011
189 / 590
dizemos que f tem um mínimo (absoluto) no ponto a ∈ D ou que
f (a) é um mínimo (absoluto) de f .
Os máximos e mínimos (absolutos) de f dizem-se extremos
absolutos de f .
António Bento (UBI)
§2.7 Propriedades fundamentais das funções contínuas
p(x) = an x + an−1 x
Sejam D ⊆ R um conjunto não vazio, fechado e limitado e
+ · · · + a1 x + a0 ,
an 6= 0, de grau ímpar, ou seja, n é um número natural ímpar. Como
lim p(x) = lim x
x→+∞
x→+∞
e
n
an−1
a1
a0
an +
+ · · · + n−1 + n
x
x
x
an−1
a1
a0
+ · · · + n−1 + n
x
x
x
lim p(x) = lim xn an +
x→−∞
x→−∞
=
=
+∞
−∞
−∞
+∞
Cálculo I
f: D →R
uma função contínua. Então f tem máximo e mínimo absolutos.
se an > 0,
se an < 0,
se an > 0,
se an < 0,
existem números reais a e b tais que p(a) < 0 e p(b) > 0. A
continuidade de p implica, pelo Teorema de Bolzano, que p tem de ter
um zero entre a e b. Assim, todos os polinómios de grau ímpar têm
pelo menos um zero (real)!
António Bento (UBI)
191 / 590
Teorema de Weierstrass
Consideremos uma função polinomial
n−1
2010/2011
§2.7 Propriedades fundamentais das funções contínuas
Exemplos (continuação)
n
Cálculo I
2010/2011
190 / 590
Corolário
Sejam a e b números reais tais que a < b e
f : [a, b] → R
uma função contínua. Então f tem máximo e mínimo absolutos.
António Bento (UBI)
Cálculo I
2010/2011
192 / 590
§2.7 Propriedades fundamentais das funções contínuas
Índice
Exemplo
Seja f : [1, 5] → R a função definida por


x − 1
f (x) = e2x−6 −1


x−3
se x ∈ [1, 3],
se x ∈]3, 5].
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
Derivadas: definição, regras de derivação e exemplos
Teoremas de Rolle, de Lagrange e de Cauchy
Derivadas de ordem superior e fórmula de Taylor
Aplicações do cálculo diferencial
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Como
lim f (x) = lim− x − 1 = 2
x→3−
e
x→3
e2x−6 −1
e2(x−3) −1
= lim+
2 = 1.2 = 2,
lim+ f (x) = lim+
x→3
x→3
x−3
x→3
2(x − 3)
temos lim f (x) = 2 = f (3). Assim, f é contínua no ponto x = 3. Além disso,
x→3
em [1, 5] \ {3} a função é contínua pois é a composição de funções contínuas.
Pelo Teorema de Weierstrass, f tem máximo e mínimo absolutos em [1, 5].
António Bento (UBI)
Cálculo I
2010/2011
193 / 590
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
Derivadas: definição, regras de derivação e exemplos
Teoremas de Rolle, de Lagrange e de Cauchy
Derivadas de ordem superior e fórmula de Taylor
Aplicações do cálculo diferencial
4
Primitivas
5
Cálculo integral em R
6
Cálculo I
2010/2011
195 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
Índice
1
António Bento (UBI)
Sejam D um subconjunto não vazio de R, f : D → R e a ∈ D um
ponto de acumulação de D. Diz-se que f é derivável ou
diferenciável em a se existe (e é finito) o limite:
f (x) − f (a)
.
x→a
x−a
lim
Tal limite (quando existe) diz-se a derivada de f no ponto a e
df
representa-se por f ′ (a), Df (a) ou ainda por
(a). Fazendo a
dx
mudança de variável x = a + h, temos
f (a + h) − f (a)
.
h→0
h
f ′ (a) = lim
Sucessões e séries
Aqui têm apenas de se considerar os valores de h tais que a + h ∈ D.
António Bento (UBI)
Cálculo I
2010/2011
194 / 590
António Bento (UBI)
Cálculo I
2010/2011
196 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
y = f (a) + f ′ (a)(x − a)
Diz-se que a função f : D → R é derivável ou diferenciável em D se
for derivável em todo o ponto de D e à nova função
f (a
(a +
+ h)
h)
f
f (a + h)
b
f (a)
f ′ : D → R,
que a cada ponto x ∈ D faz corresponder f ′ (x), chama-se derivada de
df
f e representa-se também por Df ou
.
dx
b
b
b
b
f ′ (a) = tg α
α
a a + ah + ah + ah + h
Interpretação geométrica do conceito de derivada
António Bento (UBI)
Cálculo I
2010/2011
197 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
António Bento (UBI)
Cálculo I
2010/2011
199 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
O quociente
f (a + h) − f (a)
h
representa o declive da recta que passa pelos pontos
Exemplos – funções constante
Seja f : R → R a função definida por
(a, f (a)) e (a + h, f (a + h)) .
f (x) = c,
Fazendo h tender para zero, a recta que passa nos pontos
(a, f (a)) e (a + h, f (a + h)) ,
onde c é um número real. Então
vai tender para a recta tangente ao gráfico de f e que passa no ponto
(a, f (a)). Assim, geometricamente, a derivada de uma função num
ponto do domínio é o declive da recta tangente ao gráfico da função no
ponto considerado. Portanto, a recta tangente ao gráfico de uma
função f no ponto (a, f (a)) é a recta de equação
f ′ (x) = lim
h→0
f (x + h) − f (x)
c−c
0
= lim
= lim = lim 0 = 0
h→0 h
h→0 h
h→0
h
para cada x ∈ R. Assim, f ′ é a função identicamente nula.
y = f (a) + f ′ (a)(x − a).
António Bento (UBI)
Cálculo I
2010/2011
198 / 590
António Bento (UBI)
Cálculo I
2010/2011
200 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – função logaritmo natural
Exemplos – função identidade
Seja f : ]0, +∞[ → R a função dada por f (x) = ln x. Então
Consideremos a função f : R → R definida por
f (x) = x.
h→0
=
Então, para cada x ∈ R, temos
f (x + h) − f (x)
x+h−x
h
= lim
= lim = lim 1 = 1
h→0
h→0
h→0 h
h→0
h
h
f ′ (x) = lim
=
e, portanto, f ′ : R → R é dada por
=
f ′ (x) = 1.
=
António Bento (UBI)
Cálculo I
f (x + h) − f (x)
h
ln(x + h) − ln x
lim
h→0
h
x+h
ln
x
lim
h→0
h
h
ln 1 +
x 1
lim
h→0
h/x
x
1
.
x
f ′ (x) = lim
2010/2011
201 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
António Bento (UBI)
Cálculo I
2010/2011
203 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos
Exemplos – função exponencial
A função f : R → R definida por f (x) = sen x é derivável para
qualquer x ∈ R. De facto,
Seja f : R → R a função dada por
f (x) = ex .
f (x + h) − f (x)
h
sen (x + h) − sen x
lim
h→0
h
x+h−x
x+h+x
2 sen
cos
2
2
lim
h→0
h
2x + h
sen h/2
lim
cos
h→0 h/2
2
cos x,
f ′ (x) = lim
h→0
Então
f ′ (x) =
=
=
=
=
f (x + h) − f (x)
lim
h→0
h
ex+h − ex
lim
h→0
h
h −1
e
lim ex
h→0
h
ex .
=
=
=
o que mostra que (sen x)′ = cos x.
António Bento (UBI)
Cálculo I
2010/2011
202 / 590
António Bento (UBI)
Cálculo I
2010/2011
204 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos
Consideremos a função f : R → R dada por f (x) = cos x. Atendendo a
que
=
=
=
Da+ = {x ∈ D : x > a} = D ∩ ]a, +∞[,
então diz-se que f é derivável (ou diferenciável) à direita em a se
existe e é finito o limite
f (x + h) − f (x)
h→0
h
cos (x + h) − cos x
lim
h→0
h
x+h+x
x+h−x
−2 sen
sen
2
2
lim
h→0
h
2x + h sen h/2
lim − sen
h→0
2
h/2
− sen x,
f ′ (x) = lim
=
Se f : D → R e a ∈ D é um ponto de acumulação de
lim
x→a+
f (x) − f (a)
f (a + h) − f (a)
= lim
= fd′ (a).
x−a
h
h→0+
Tendo em conta as propriedades dos limites, resulta imediatamente,
para pontos a ∈ D que são pontos de acumulação de Da− e de Da+ , que
f é derivável em a se e só se f é derivável à esquerda e à direita em a e
fe′ (a) = fd′ (a).
temos que (cos x)′ = − sen x.
António Bento (UBI)
Cálculo I
2010/2011
205 / 590
António Bento (UBI)
§3.1 Derivadas: definição, regras de derivação e exemplos
Cálculo I
2010/2011
207 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos
Seja f : R → R a função definida por
Sejam f : D → R e a ∈ D tal que a é ponto de acumulação de
f (x) = |x| .
Da− = {x ∈ D : x < a} = D ∩ ] − ∞, a[.
Diz-se que f é derivável (ou diferenciável) à esquerda em a se
existe e é finito o limite
lim
x→a−
f (x) − f (a)
f (a + h) − f (a)
= lim−
= fe′ (a).
x−a
h
h→0
Então
fe′ (0) = lim−
x→0
e
f (x) − f (0)
|x|
x
= lim−
= lim− − = −1
x−0
x
x
x→0
x→0
f (x) − f (0)
|x|
x
= lim
= lim
= 1,
+
+
x−0
x
x→0
x→0 x
o que mostra que f não é derivável no ponto 0.
fd′ (0) = lim
x→0+
António Bento (UBI)
Cálculo I
2010/2011
206 / 590
António Bento (UBI)
Cálculo I
2010/2011
208 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Regras de derivação
Exemplos
Sejam f, g : D → R funções deriváveis em a ∈ D e k ∈ R. Então
Consideremos a função f : R → R definida por
f (x) =

x sen 1

0
x
i) f + g é derivável em a e
(f + g)′ (a) = f ′ (a) + g′ (a);
se x 6= 0,
se x = 0.
ii) kf é derivável em a e
Esta função não é diferenciável à direita, nem à esquerda do ponto 0,
pois não existe
x sen (1/x)
1
= lim sen ,
lim
+
+
x
x
x→0
x→0
nem
1
x sen (1/x)
lim
= lim sen .
−
−
x
x
x→0
x→0
António Bento (UBI)
Cálculo I
2010/2011
209 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
(kf )′ (a) = kf ′ (a);
iii) f.g é derivável em a e
(f.g)′ (a) = f ′ (a) g(a) + g′ (a) f (a);
iv) se g(a) 6= 0,
f
é derivável em a e
g f ′ (a) g(a) − g′ (a) f (a)
f ′
(a) =
.
g
g2 (a)
António Bento (UBI)
Cálculo I
2010/2011
211 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
Propriedades
Se f : D → R é uma função derivável em a ∈ D, então f é contínua
nesse ponto.
Demonstração das regras de derivação
i) Basta observar que
(f + g)(x) − (f + g)(a)
f (x) − f (a) g(x) − g(a)
lim
= lim
+
x→a
x→a
x−a
x−a
x−a
′
′
= f (a) + g (a).
Observação
O recíproco desta propriedade é falso. A função
ii) Basta ter em conta que
f :R→R
lim
dada por
x→a
f (x) = |x|
(kf )(x) − (kf )(a)
f (x) − f (a)
= lim k
x→a
x−a
x−a
= k f ′ (a).
é contínua no ponto 0, mas não é derivável nesse ponto.
António Bento (UBI)
Cálculo I
2010/2011
210 / 590
António Bento (UBI)
Cálculo I
2010/2011
212 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – funções polinomiais
A função f : R → R definida por
Demonstração das regras de derivação (continuação)
f (x) = xn
iii) Basta atender a que
lim
x→a
f (x)g(x) − f (a)g(a)
(f g)(x) − (f g)(a)
= lim
x→a
x−a
x−a
f (x)g(x) − f (a)g(x) + f (a)g(x) − f (a)g(a)
= lim
x→a
x−a
f (x) − f (a)
g(x) − g(a)
= lim
g(x) + f (a)
x→a
x−a
x−a
′
′
= f (a)g(a) + f (a)g (a).
Na última igualdade foi usado o facto de g ser contínua em a.
derivável em todos os pontos de R e
f ′ (x) = nxn−1 .
Usando esta última igualdade, tem-se que a derivada da função
definida por
p(x) = an xn + an−1 xn−1 + · · · + a2 x2 + a1 x + a0
é dada por
p′ (x) = nan xn−1 + (n − 1) an−1 xn−2 + · · · + 2a2 x + a1 .
António Bento (UBI)
Cálculo I
2010/2011
213 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
lim
x→a
g
f g
x−a
(a)
=
=
=
=
f (x)
f (a)
−
g(x)
g(a)
lim
x→a
x−a
f (x)g(a) − f (a)g(x)
g(x)g(a)
lim
x→a
x−a
h
i
1
f (x)g(a) − f (a)g(x)
lim
x→a g(x)g(a)
x−a
h 1
i
f (x)g(a) − f (a)g(a) + f (a)g(a) − f (a)g(x)
lim
x→a g(x)g(a)
x−a
= lim
x→a
=
h
1
g(x)g(a)
2010/2011
215 / 590
Exemplos – tangente
iv) Do mesmo modo temos
(x) −
Cálculo I
§3.1 Derivadas: definição, regras de derivação e exemplos
Demonstração das regras de derivação (continuação).
f António Bento (UBI)
f (x) − f (a)
g(x) − g(a)
g(a) − f (a)
x−a
x−a
f ′ (a) g(a) − g ′ (a) f (a)
.
g 2 (a)
A derivada da tangente pode ser calculada da seguinte forma:
(tg x)′ =
=
=
=
i
=
=
sen x ′
cos x
(sen x)′ cos x − (cos x)′ sen x
cos2 x
cos x. cos x − (− sen x) sen x
cos2 x
2
cos x + sen2 x
cos2 x
1
cos2 x
sec2 x.
Na última igualdade usou-se o facto de g ser contínua em a.
António Bento (UBI)
Cálculo I
2010/2011
214 / 590
António Bento (UBI)
Cálculo I
2010/2011
216 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – cotangente
Derivada da função composta
Do mesmo modo temos
(cotg x)′ =
=
=
=
=
=
Sejam Df e Dg dois subconjuntos não vazios de R e
cos x ′
sen x
(cos x)′ sen x − (sen x)′ cos x
sen2 x
− sen x. sen x − (cos x) cos x
sen2 x
2
sen x + cos2 x
−
sen2 x
1
−
sen2 x
− cosec2 x.
António Bento (UBI)
Cálculo I
f : Df → R e g : Dg → R
funções tais que
f (Df ) ⊆ Dg .
Suponhamos que a ∈ Df é um ponto de acumulação de Df e b = f (a) é
um ponto de acumulação de Dg . Se f é derivável em a e g é derivável
em b, então g ◦ f é derivável em a e
(g ◦ f )′ (a) = g′ (f (a)) f ′ (a) = g′ (b) f ′ (a).
2010/2011
217 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
António Bento (UBI)
Cálculo I
2010/2011
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – seno e coseno hiperbólicos
Exemplos
Atendendo a que
Seja f : R → R a função definida por f (x) = 2x2 + 5
usando a derivada da função composta, temos
e−x
tem-se
′
=
1
ex
′
=
100
1′ ex −(ex )′ 1
− ex
1
−x
=
2
2 = − ex = − e ,
x
x
(e )
(e )
99 f ′ (x) = 100 2x2 + 5
(senh x)′ =
2
!′
=
(ex )′
−
2
′
(e−x )
=
ex + e−x
2
99
(cosh x) =
António Bento (UBI)
ex + e−x
2
!′
=
′
ex − e−x
(ex )′ + (e−x )
=
= senh x.
2
2
Cálculo I
2010/2011
218 / 590
4x
99
= 400x 2x2 + 5
= cosh x
e
′
. Então,
′
2x2 + 5
= 100 2x2 + 5
ex − e−x
219 / 590
.
Consideremos a função g : R → R dada por g(x) = sen (ex +1). A sua
derivada é dada por
g′ (x) = cos (ex +1) (ex +1)′ = cos (ex +1) ex = ex cos (ex +1) .
António Bento (UBI)
Cálculo I
2010/2011
220 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos
Exemplos
2
A função h : R → R definida por h(x) = e3 cos x tem derivada em todos
os pontos de R e
h′ (x) = e3 cos x
= e3 cos x
= e3 cos x
2
3 cos x2
2
2
−3 sen x2
−3 sen x2
2 3 cos x2
= −6x sen x e
António Bento (UBI)
′
x2
2x
Se f é uma função real de variável real diferenciável, então
h
ef (x)
= f ′ (x) ef (x) ,
[sen (f (x))]′ = f ′ (x) cos (f (x))
′
e
[cos (f (x))]′ = −f ′ (x) sen (f (x)) .
.
Cálculo I
i′
2010/2011
221 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
António Bento (UBI)
Cálculo I
2010/2011
223 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – função exponencial e função logarítmica
Para a função exponencial temos
x)
(ax )′ = eln(a
′
Derivada da função inversa
= ex ln a
′
Sejam f uma função diferenciável e injectiva definida num intervalo
I ⊆ R e a ∈ I. Se
f ′ (a) 6= 0,
= ex ln a ln a = ax ln a.
Para a função logarítmica usando a igualdade
então f −1 é diferenciável em b = f (a) e
loge x = loga x loge a
temos
(loga x)′ =
António Bento (UBI)
ln x
ln a
′
=
f −1
(ln x)′
1/x
1
=
=
.
ln a
ln a
x ln a
Cálculo I
2010/2011
222 / 590
António Bento (UBI)
′
(b) =
1
f ′ (f −1 (b))
Cálculo I
=
1
f ′ (a)
.
2010/2011
224 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – arco seno
Exemplos – raízes
Consideremos a função g : [−1, 1] → [−π/2, π/2] definida por
A função g :]0, +∞[→]0, +∞[ definida por
√
g(x) = n x
g(x) = arc sen x.
A função g é a função inversa da função f : [−π/2, π/2] → [−1, 1] dada por
f (y) = sen y.
é a função inversa da função f :]0, +∞[→]0, +∞[ definida por
Além disso, f ′ (y) = cos y 6= 0 para y ∈ ]−π/2, π/2[. Assim, escrevendo
y = arc sen x, ou seja, x = sen y, temos
′
1
1
g ′ (x) = f −1 (x) =
=
.
cos y
(sen y)′
f (y) = y n .
Como f ′ (y) = ny n−1 6= 0 para qualquer y ∈ ]0, +∞[ temos, fazendo
y = g(x),
g′ (x) = f −1
′
1
(x) =
f ′ (y)
=
2
2
Tendo em
√ conta que sen y + cos y = 1 e que y ∈ ]−π/2, π/2[, obtemos
2
cos y = 1 − x e, por conseguinte, para x ∈ ]−π/2, π/2[ temos
1
′
(arc sen x) = √
.
1 − x2
1
1
= √
.
n
n−1
ny
n xn−1
Nos pontos x = −1 e x = 1 a função não tem derivada lateral à direita, nem
derivada lateral à esquerda, respectivamente.
António Bento (UBI)
Cálculo I
2010/2011
225 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
António Bento (UBI)
Cálculo I
2010/2011
227 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – arco coseno
Exemplos – logaritmo natural
A função g : [−1, 1] → [0, π] definida por
Do mesmo modo, a função g : ]0, +∞[→ R definida por
g(x) = arc cosx
g(x) = ln x
é a inversa da função f : [0, π] → [−1, 1] definida por
f (y) = cos y.
é a inversa da função f : R →]0, +∞[ definida por
Atendendo a que f ′ (y) = − sen y 6= 0 para cada y ∈]0, π[ vem
1
(arc cosx)′ =
− sen y
f (y) = ey .
Como f ′ (y) = ey 6= 0 para qualquer y ∈ R e y = ln x temos
g′ (x) = f −1
António Bento (UBI)
′
e, como sen2 y + cos2 y = 1 e y ∈]0, π[, temos sen y = 1 − cos2 y o que
implica
1
1
(arc cosx)′ = − p
= −√
.
2
1 − cos y
1 − x2
p
1
1
1
(x) = ′
= y = .
f (y)
e
x
Cálculo I
2010/2011
226 / 590
António Bento (UBI)
Cálculo I
2010/2011
228 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
§3.1 Derivadas: definição, regras de derivação e exemplos
Exemplos – arco tangente
Tabela de derivadas
A função g : ]−π/2, π/2[ → R definida por
[αu(x)]′ = α u′ (x), α ∈ R
g(x) = arc tg x
é a inversa da função f : R → ]−π/2, π/2[ definida por
′
[u(x) v(x)] = u′ (x) v(x) + u(x) v ′ (x)
g(y) = tg y.
Como g′ (y) =
[(u(x))α ] = α u′ (x) [u(x)]α−1 , α ∈ R
′
1
6= 0 para y ∈ ]−π/2, π/2[ temos
cos2 y
(arc tg x)′ =
u(x) ′
= u′ (x) eu(x)
e
1
1
1
=
=
.
1
1 + tg2 y
1 + x2
cos2 y
António Bento (UBI)
Cálculo I
[u(x) + v(x)]′ = u′ (x) + v ′ (x)
229 / 590
′
=
u′ (x) v(x) − u(x) v ′ (x)
[v(x)]
2
hp
i′
u′ (x)
u(x) = p
2 u(x)
′
u′ (x)
u(x)
[loga (u(x))] =
António Bento (UBI)
§3.1 Derivadas: definição, regras de derivação e exemplos
u(x)
v(x)
[ln (u(x))]′ =
u(x) ′
a
= u′ (x)au(x) ln a
2010/2011
u′ (x)
u(x) ln a
Cálculo I
2010/2011
231 / 590
§3.1 Derivadas: definição, regras de derivação e exemplos
Tabela de derivadas (continuação)
[sen (u(x))]′ = u′ (x) cos [u(x)]
Exemplos – arco cotangente
Do mesmo modo tem-se
u′ (x)
cos2 [u(x)]
′
[tg (u(x))] =
(arc cotg x)′ = −
1
.
1 + x2
[cos (u(x))]′ = −u′ (x) sen [u(x)]
′
[cotg (u(x))] = −
u′ (x)
′
[arc sen (u(x))] = q
2
1 − [u(x)]
u′ (x)
′
[arc cos (u(x))] = − q
2
1 − [u(x)]
u′ (x)
′
[arc tg (u(x))] =
1 + [u(x)]
′
[arc cotg (u(x))] = −
2
′
Cálculo I
2010/2011
230 / 590
António Bento (UBI)
u′ (x)
1 + [u(x)]
2
′
[senh (u(x))] = u′ (x) cosh [u(x)]
António Bento (UBI)
u′ (x)
sen2 [u(x)]
[cosh (u(x))] = u′ (x) senh [u(x)]
Cálculo I
2010/2011
232 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
Derivadas: definição, regras de derivação e exemplos
Teoremas de Rolle, de Lagrange e de Cauchy
Derivadas de ordem superior e fórmula de Taylor
Aplicações do cálculo diferencial
A interpretação geométrica de f ′ (c) = 0 corresponde a que a recta
tangente ao gráfico de f no ponto (c, f (c)) é horizontal. Tendo isto em
conta, podemos interpretar geometricamente o Teorema de Rolle da
seguinte forma.
y
b
f (a) = f (b)
b
b
b
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
a
x
c
c′
b
Interpretação geométrica do Teorema de Rolle
António Bento (UBI)
Cálculo I
2010/2011
233 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
António Bento (UBI)
Cálculo I
2010/2011
235 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Teorema de Rolle
Sejam a e b números reais tais que a < b e seja
Corolários do Teorema de Rolle
f : [a, b] → R
Sejam I um intervalo e
f: I →R
uma função contínua em [a, b] e diferenciável em ]a, b[. Se
uma função diferenciável em I. Então
f (a) = f (b),
a) entre dois zeros de f existe pelo menos um zero da derivada;
b) entre dois zeros consecutivos da derivada de f existe, quando
muito, um zero da função.
então existe
tal que
c ∈ ]a, b[
f ′ (c) = 0.
António Bento (UBI)
Cálculo I
2010/2011
234 / 590
António Bento (UBI)
Cálculo I
2010/2011
236 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Corolários do Teorema de Lagrange
Teorema do valor médio de Lagrange
Sejam I um intervalo de R e f, g : I → R funções diferenciáveis em I.
Sejam a e b números reais tais que a < b e
a) Se
f : [a, b] → R
então f é constante.
uma função contínua em [a, b] e diferenciável em ]a, b[. Então existe
b) Se
f ′ (x) = g ′ (x) para qualquer x ∈ I,
c ∈ ]a, b[
então a diferença f − g é constante em I.
f (b) − f (a) = f ′ (c) (b − a) ,
c) Se f ′ (x) > 0 para qualquer x ∈ I, então f é estritamente crescente em
I, ou seja, para quaisquer x, y ∈ I,
f (b) − f (a)
= f ′ (c).
b−a
d) Se f ′ (x) < 0 para qualquer x ∈ I, então f é estritamente decrescente
em I, ou seja, para quaisquer x, y ∈ I,
tal que
ou seja,
f ′ (x) = 0 para qualquer x ∈ I,
António Bento (UBI)
se x > y, então f (x) > f (y).
se x > y, então f (x) < f (y).
Cálculo I
2010/2011
237 / 590
António Bento (UBI)
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Cálculo I
2010/2011
239 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
f (b) − f (a)
é o declive da recta que
b−a
passa nos pontos (a, f (a)) e (b, f (b)). O que o Teorema de Lagrange
nos diz é que existe uma recta tangente ao gráfico de f paralela à recta
que passa nos pontos (a, f (a)) e (b, f (b)).
Geometricamente, o quociente
Teorema de Cauchy
Sejam a e b números reais tais que a < b e
f, g : [a, b] → R
y
funções contínuas em [a, b] e diferenciáveis em ]a, b[. Se
b
g′ (x) 6= 0 para qualquer x ∈ ]a, b[,
f (b)
f (a)
b
então existe
b
tal que
a
c
x
b
c ∈ ]a, b[
f (b) − f (a)
f ′ (c)
= ′ .
g(b) − g(a)
g (c)
Interpretação geométrica do Teorema de Lagrange
António Bento (UBI)
Cálculo I
2010/2011
238 / 590
António Bento (UBI)
Cálculo I
2010/2011
240 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Regra de Cauchy quando x → +∞
Regra de Cauchy
Sejam a um número real e f, g : ]a, +∞[→ R funções diferenciáveis em
]a, +∞[ e tais que
Sejam a e b números reais tais que a < b e f, g : ]a, b[→ R funções
diferenciáveis em ]a, b[ tais que
g′ (x) 6= 0 para cada x ∈ ]a, b[.
Suponhamos que
Suponhamos que
lim f (x) = lim g(x) = 0
lim f (x) = lim g(x) = 0
x→a+
x→+∞
x→a+
lim |f (x)| = lim |g(x)| = +∞.
f ′ (x)
Se lim ′
= L, então
x→a+ g (x)
António Bento (UBI)
lim |f (x)| = lim |g(x)| = +∞.
x→a+
x→+∞
Se lim
x→+∞
f (x)
lim
= L.
+
x→a g(x)
Cálculo I
x→+∞
ou que
ou que
x→a+
g′ (x) 6= 0 para cada x ∈]a, +∞[.
f ′ (x)
g′ (x)
x→+∞
= L, então
f (x)
= L.
x→+∞ g(x)
lim
2010/2011
241 / 590
António Bento (UBI)
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Cálculo I
2010/2011
243 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Observações
Observação
a) O resultado continua válido se substituirmos
O resultado continua válido se substituirmos
lim
lim
x→a+
x→+∞
por
por
lim− .
lim ,
x→b
x→−∞
b) O resultado também é válido quando calculamos o limite em pontos
interiores do domínio das funções.
sendo neste caso o domínio das funções um intervalo do tipo ] − ∞, a[.
António Bento (UBI)
Cálculo I
2010/2011
242 / 590
António Bento (UBI)
Cálculo I
2010/2011
244 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Exemplos de aplicação da regra de Cauchy
Exemplos de aplicação da regra de Cauchy (continuação)
1) Como
2) (continuação) Temos de aplicar novamente a regra de Cauchy
cos x − 1
0
lim
= ,
2
x→0
x
0
temos pela regra de Cauchy
esen x − ex
x→0 sen x − x
′
cos2 x − sen x esen x − ex
= lim
′
x→0
[− sen x]
(−2 sen x cos x − cos x) esen x + cos2 x − sen x cos x esen x − ex
= lim
x→0
− cos x
−1 + 1 − 1
=
=1
−1
lim
cos x − 1
(cos x − 1)′
=
lim
x→0
x→0
x2
(x2 )′
− sen x
= lim
x→0
2x
1 sen x
= lim −
x→0 2 x
1
= − .1
2
1
=− .
2
lim
António Bento (UBI)
Cálculo I
Este limite podia ter sido calculado mais facilmente da seguinte
forma
esen x − ex
esen x−x −1
lim
= lim ex
= e0 .1 = 1.
x→0 sen x − x
x→0
sen x − x
2010/2011
245 / 590
António Bento (UBI)
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
3) Vejamos que
esen x − ex
(esen x − ex )′
cos x esen x − ex
0
lim
= lim
=
lim
= .
′
x→0 sen x − x
x→0 (sen x − x)
x→0
cos x − 1
0
Aplicando novamente a regra de Cauchy vem
esen x − ex
(cos x esen x − ex )′
lim
= lim
x→0 sen x − x
x→0
(cos x − 1)′
ln x
= 0, a > 0.
xa
lim
x→+∞
Como
ln x
+∞
=
,
a
x→+∞ x
+∞
aplicando a regra de Cauchy temos
lim
1
ln x
(ln x)′
x = lim 1 = 1 = 0.
lim
= lim
= lim
′
a
a
x→+∞ x
x→+∞ (x )
x→+∞ axa−1
x→+∞ axa
+∞
− sen x esen x + cos2 x esen x − ex
x→0
− sen x
0
= .
0
= lim
2010/2011
247 / 590
Exemplos de aplicação da regra de Cauchy (continuação)
esen x − ex
0
2) Como lim
= , usando a regra de Cauchy temos
x→0 sen x − x
0
Cálculo I
2010/2011
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Exemplos de aplicação da regra de Cauchy (continuação)
António Bento (UBI)
Cálculo I
246 / 590
António Bento (UBI)
Cálculo I
2010/2011
248 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Exemplos de aplicação da regra de Cauchy (continuação)
Exemplos de aplicação da regra de Cauchy (continuação)
4) Vejamos como calcular lim+
x→1
lim+
x→1
√
1
− cotg x = ∞ − ∞. Transformando esta
x
indeterminação na seguinte
5) Calculemos agora lim
x − 1 ln (ln x) = 0 × (−∞). Como
√
x − 1 ln (ln x) = lim+
x→1
ln (ln x)
−1/2
(x − 1)
=
x→0
1
1
cos x
sen x − x cos x
0
− cotg x = lim −
= lim
= ,
x→0 x
x→0 x
sen x x→0
x sen x
0
∞
,
∞
lim
podemos aplicar a regra de Cauchy. Assim,
podemos usar a regra de Cauchy e temos
1/x
√
[ln (ln x)]
ln x
lim x − 1 ln (ln x) = lim+ h
i′ = lim+
−3/2
x→1+
x→1
−1/2
x→1
(x
−
1)
(x − 1)
−
2
3/2
2 (x − 1)
0
= lim+ −
= .
x→1
x ln x
0
′
António Bento (UBI)
Cálculo I
2010/2011
249 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
sen x − x cos x
(sen x − x cos x)′
= lim
x→0
x→0
x sen x
(x sen x)′
cos x − cos x + x sen x
= lim
x→0
sen x + x cos x
x sen x
= lim
x→0 sen x + x cos x
0
= .
0
lim
António Bento (UBI)
Cálculo I
2010/2011
251 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Exemplos de aplicação da regra de Cauchy (continuação)
Exemplos de aplicação da regra de Cauchy (continuação)
3/2
(x − 1)
0
4) (continuação) Atendendo a que lim+
= , aplicando
x→1
ln x
0
novamente a regra de Cauchy temos
1/2
′
3 (x − 1)
3/2
3/2
(x
−
1)
(x − 1)
2
lim+
= lim+
= lim+
′
1
x→1
x→1
x→1
ln x
(ln x)
x
3x (x − 1)1/2
= lim+
= 0,
x→1
2
5) (continuação) Aplicando novamente a regra de Cauchy temos
sen x − x cos x
(x sen x)′
= lim
x→0 (sen x + x cos x)′
x→0
x sen x
sen x + x cos x
= lim
x→0 cos x + cos x − x sen x
0
=
2
= 0
lim
pelo que
lim+
x→1
o que implica
3/2
√
2 (x − 1)
x − 1 ln (ln x) = lim+ −
x→1
x ln x
lim
x→0
3/2
= lim+ −
x→1
António Bento (UBI)
Cálculo I
2 (x − 1)
x
ln x
1
− cotg x = 0.
x
= 0.
2010/2011
250 / 590
António Bento (UBI)
Cálculo I
2010/2011
252 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
Índice
Exemplos de aplicação da regra de Cauchy (continuação)
6) Calculemos agora
lim+ (sen x)x .
x→0
Neste caso temos uma indeterminação do tipo 00 . Atendendo a que
x
lim (sen x)x = lim eln[(sen x)
x→0+
x→0+
]
x→0+
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
Derivadas: definição, regras de derivação e exemplos
Teoremas de Rolle, de Lagrange e de Cauchy
Derivadas de ordem superior e fórmula de Taylor
Aplicações do cálculo diferencial
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
x→0+
x→0+
x→0+
Funções reais de variável real: generalidades e exemplos
= lim ex ln(sen x) ,
basta calcular lim x ln (sen x). Como
lim x ln (sen x) = lim
1
ln (sen x)
0
= ,
1
0
x
podemos aplicar a regra de Cauchy.
António Bento (UBI)
Cálculo I
2010/2011
253 / 590
§3.2 Teoremas de Rolle, de Lagrange e de Cauchy
António Bento (UBI)
Cálculo I
2010/2011
255 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
Sejam D um subconjunto não vazio de R e
Exemplos de aplicação da regra de Cauchy (continuação)
f: D →R
6) (continuação) Assim,
cos x
(ln (sen x))′
sen
x
lim x ln (sen x) = lim
= lim
′
1
1
x→0+
x→0+
x→0+
− 2
x
x
x
= lim
(−x cos x) = 1.0 = 0
x→0+ sen x
uma função diferenciável em D. Se f ′ é diferenciável em a ∈ D, então
diz-se que f é duas vezes diferenciável em a e a derivada de f ′ em a
designa-se por segunda derivada de f em a e representa-se por
f ′′ (a) ou
e, portanto,
d2 f
(a) ou ainda D2 f (a)
dx2
e é dada por
lim (sen x)x = lim+ ex ln(sen x) = e0 = 1.
x→0+
António Bento (UBI)
′
Cálculo I
2010/2011
f ′ (x) − f ′ (a)
f ′ (a + h) − f ′ (a)
= lim
.
x→a
h→0
x−a
h
f ′′ (a) = f ′ (a) = lim
x→0
254 / 590
António Bento (UBI)
Cálculo I
2010/2011
256 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
§3.3 Derivadas de ordem superior e fórmula de Taylor
Exemplos
Mais geralmente, se existirem as derivadas de f até à ordem n − 1 e as
representarmos por
f ′ , f ′′ , . . . , f (n−1)
e f (n−1) é derivável em a, então diz-se que f tem derivada de ordem
n em a e
f
(n)
f (n−1) (x) − f (n−1) (a)
(a) = lim
x→a
x−a
(n−1)
f
(a + h) − f (n−1) (a)
= lim
.
h→0
h
a) A função f : R → R definida por
f (x) = xm ,
m ∈ N, é uma função de classe C ∞ . De facto
f
(n)
(x) =

m−n


m (m − 1) . . . (m − (n − 1)) x
m!


0
se n < m;
se n = m;
se n > m.
Mais geralmente, qualquer polinómio p : R → R dado por
p(x) = am xm + am−1 xm−1 + · · · + a2 x2 + a1 x + a0
é de classe C ∞ .
António Bento (UBI)
Cálculo I
2010/2011
257 / 590
António Bento (UBI)
§3.3 Derivadas de ordem superior e fórmula de Taylor
Cálculo I
2010/2011
259 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
Uma função f : D → R diz-se de classe C n , e escreve-se
Exemplos (continuação)
f ∈ C n (D),
b) Se
se f é n vezes diferenciável em D e a derivada de ordem n, f (n) é
contínua em D.
p, q : R → R
são dois polinómios, então fazendo
Por extensão, escreve-se
D = {x ∈ R : q(x) 6= 0}
0
f ∈ C (D) ou f ∈ C(D)
tem-se que a função f : D → R definida por
para designar que f é contínua em D.
Se f admite derivadas de todas as ordens em D, então dizemos que f é
indefinidamente diferenciável ou de classe C ∞ e usa-se a notação
f (x) =
e, portanto,
f ∈ C ∞ (D).
f ∈ C ∞ (D).
António Bento (UBI)
Cálculo I
p(x)
q(x)
2010/2011
258 / 590
António Bento (UBI)
Cálculo I
2010/2011
260 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
§3.3 Derivadas de ordem superior e fórmula de Taylor
Exemplos (continuação)
e) Do mesmo modo, a função coseno é uma função de classe C ∞ . De
facto, se
f (x) = cos x,
Exemplos (continuação)
c) A função exponencial é de classe C ∞ pois fazendo
f (x) = ex
temos
temos
f (n) (x) =
f (n) (x) = ex .
António Bento (UBI)
Cálculo I
2010/2011
261 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor


− sen x




 − cos x

sen x




 cos x
António Bento (UBI)
se
se
se
se
n = 4k − 3, k ∈ N;
n = 4k − 2, k ∈ N;
n = 4k − 1, k ∈ N;
n = 4k, k ∈ N.
Cálculo I
2010/2011
263 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
Exemplos (continuação)
f ) A função f1 : R → R definida 
por
x2 sen 1
f1 (x) =
x
0
Exemplos (continuação)
d) A função seno é uma função de classe C ∞ . De facto, fazendo
f (x) = sen x,
temos
f (n) (x) =


cos x




 − sen x

− cos x




 sen x
se
se
se
se
n = 4k − 3, k ∈ N;
n = 4k − 2, k ∈ N;
n = 4k − 1, k ∈ N;
n = 4k, k ∈ N;
o que mostra que a função seno pertence a C ∞ (R).
António Bento (UBI)
Cálculo I
2010/2011
262 / 590
se x 6= 0;
se x = 0;
é diferenciável, mas a primeira derivada não é contínua. Como
′
1
1
1
1
1
1
2
2
x sen
= 2x sen + x − 2 cos = 2x sen − cos
x
x
x
x
x
x
e
1
x2 sen − 0
f1 (x) − f1 (0)
1
′
x
f1 (0) = lim
= lim
= lim x sen = 0,
x→0
x→0
x→0
x−0
x−0
x
temos

2x sen 1 − cos 1 se x 6= 0;
f1′ (x) =
x
x
0
se x = 0.
António Bento (UBI)
Cálculo I
2010/2011
264 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
§3.3 Derivadas de ordem superior e fórmula de Taylor
Exemplos (continuação)
f ) (continuação) Vimos que

2x sen 1 − cos 1
′
f1 (x) =
x
x

0
Fórmula de Taylor (com resto de Lagrange)
se x 6= 0;
Sejam I um intervalo,
se x = 0.
Como não existe
1
lim cos ,
x→0
x
′
a função f1 não é contínua. Assim, f1 é diferenciável, mas não é de
classe C 1 . Mais geral, a função fk : R → R definida por

x2k sen 1
se x 6= 0;
fk (x) =
x

0
se x = 0;
C n,
f: I →R
uma função de classe
n + 1 vezes diferenciável em int I e a um
ponto de I. Para cada x ∈ I \ {a}, existe c estritamente entre a e x tal
que
f (x) = f (a)+f ′ (a) (x − a) +
f (n) (a)
f (n+1) (c)
f ′′ (a)
(x − a)2 +· · ·+
(x − a)n +
(x − a)n+1 .
2!
n!
(n + 1)!
tem derivadas até à ordem k, mas não é de classe C k .
António Bento (UBI)
Cálculo I
2010/2011
265 / 590
António Bento (UBI)
§3.3 Derivadas de ordem superior e fórmula de Taylor
f, g : D ⊆ R → R
pn (x) = f (a) + f ′ (a) (x − a) +
têm derivada até à ordem n, então os mesmo acontece com
f +g
e
(x) =
n
X
n
j=0
j
!
resto Lagrange de ordem n da função f em torno de x = a.
f
(j)
(x)g
(n−j)
(x),
onde f (0) = f e g(0) = g. Esta igualdade é conhecida por fórmula
de Leibnitz.
António Bento (UBI)
Cálculo I
f ′′ (a)
f (n) (a)
(x − a)2 + · · · +
(x − a)n
2!
n!
chamamos polinómio de Taylor de grau n da função f em torno de
x=aea
f (n+1) (c)
Rn (x) =
(x − a)n+1
(n + 1)!
e fg
(f + g)(n) (x) = f (n) (x) + g(n) (x)
(f g)
267 / 590
A
g) Se
(n)
2010/2011
§3.3 Derivadas de ordem superior e fórmula de Taylor
Exemplos (continuação)
e
Cálculo I
2010/2011
266 / 590
Se a = 0 a fórmula de Taylor designa-se por fórmula de Mac-Laurin
e o polinómio de Taylor designa-se por polinómio de Mac-Laurin.
António Bento (UBI)
Cálculo I
2010/2011
268 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
§3.3 Derivadas de ordem superior e fórmula de Taylor
Ao polinómio de Taylor de grau um de uma função f em torno de a
chamamos linearização ou aproximação linear de f em torno de x = a, ou
seja, a função dada por
Exemplos (continuação)
2) Seja f a função seno. Então
L(x) = f (a) + f ′ (a)(x − a)
é a linearização de f em torno de x = a. Nestas condições escrevemos
f
f (x) ≈ f (a) + f ′ (a)(x − a).
Ao polinómio de Taylor de grau dois de uma função f em torno de x = a, isto
é, à função dada por
chamamos aproximação quadrática de f em torno de x = a e escrevemos
f ′′ (a)
(x − a)2 .
2
f (x) ≈ f (a) + f ′ (a)(x − a) +
António Bento (UBI)
Cálculo I
2010/2011
269 / 590
(
(−1)k+1
0
se n = 2k − 1, k ∈ N;
se n = 2k, k ∈ N;
e, portanto,
x2n+1
x3 x5
+
+ · · · + (−1)n
+ R2n+1 (x).
3!
5!
(2n + 1)!
Assim, neste exemplos as aproximações linear e quadrática são
iguais:
sen x ≈ x.
António Bento (UBI)
§3.3 Derivadas de ordem superior e fórmula de Taylor
Cálculo I
2010/2011
271 / 590
§3.3 Derivadas de ordem superior e fórmula de Taylor
Exemplos
Exemplos (continuação)
1) Seja f a função exponencial. Atendendo a que f (n) (x) = ex para cada
n ∈ N e, portanto, f (n) (0) = e0 = 1, o polinómio de Mac-Laurin de grau n
é dado por
f
(0) n−1 f (0) n
f (0) 2
x + ···+
x
+
x
pn (x) = f (0) + f (0) x +
2!
(n − 1)!
n!
x2
xn−1
xn
= 1+x+
+ ··· +
+
2!
(n − 1)!
n!
(n−1)
′′
3) Se f é a função coseno, então
f
(n)
′
ex ≈ 1 + x
Cálculo I
(0) =
(
(−1)k
0
se n = 2k, k ∈ N;
se n = 2k − 1, k ∈ N;
cos x = 1 −
x2 x4
x2n
+
+ · · · + (−1)n
+ R2n (x)
2!
4!
(2n)!
e temos
x2
2
como aproximações linear e quadrática, respectivamente.
cos x ≈ 1
e a seguinte aproximação quadrática
ex ≈ 1 + x +
(n)
e, consequentemente,
e, por conseguinte, temos a seguinte aproximação linear
António Bento (UBI)
(0) =
sen x = x −
f ′′ (a)
(x − a)2 ,
2
Q(x) = f (a) + f ′ (a)(x − a) +
(n)
x2
.
2
2010/2011
270 / 590
António Bento (UBI)
e
cos x ≈ 1 −
Cálculo I
2010/2011
272 / 590
§3.4 Aplicações do cálculo diferencial
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
Derivadas: definição, regras de derivação e exemplos
Teoremas de Rolle, de Lagrange e de Cauchy
Derivadas de ordem superior e fórmula de Taylor
Aplicações do cálculo diferencial
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Já vimos que para estudar a monotonia de uma função basta estudar o
sinal da primeira derivada. Isso é consequência de corolários do
Teorema de Lagrange:
Corolários do Teorema de Lagrange
Sejam I um intervalo de R e f : I → R uma função diferenciável em I.
a) Se f ′ (x) > 0 para qualquer x ∈ I, então f é estritamente
crescente em I, ou seja, para quaisquer x, y ∈ I,
se x > y, então f (x) > f (y).
b) Se f ′ (x) < 0 para qualquer x ∈ I, então f é estritamente
decrescente em I, ou seja, para quaisquer x, y ∈ I,
se x > y, então f (x) < f (y).
António Bento (UBI)
Cálculo I
2010/2011
273 / 590
António Bento (UBI)
§3.4 Aplicações do cálculo diferencial
Cálculo I
2010/2011
275 / 590
§3.4 Aplicações do cálculo diferencial
Sejam D um subconjunto não vazio de R, f : D → R uma função e
a ∈ D. Diz-se que a função f tem um máximo local ou relativo no
ponto a ou que f (a) é um máximo local ou relativo da função f se
existir um ε > 0 tal que
Nesta secção vamos ver aplicações das derivadas em termos de
f (x) 6 f (a) qualquer que seja x ∈ ]a − ε, a + ε[ ∩ D.
• monotonia de uma função;
• extremos locais de uma função;
Do mesmo modo, diz-se que a função f tem um mínimo local ou
relativo no ponto a ou que f (a) é um mínimo local ou relativo da
função f se existir um ε > 0 tal que
• convexidade e pontos de inflexão de uma função.
f (x) > f (a) qualquer que seja x ∈ ]a − ε, a + ε[ ∩ D.
Diz-se que f tem um extremo local ou relativo no ponto a ou que
f (a) é um extremo local ou relativo da função f se f tiver um
máximo ou um mínimo local no ponto a.
António Bento (UBI)
Cálculo I
2010/2011
274 / 590
António Bento (UBI)
Cálculo I
2010/2011
276 / 590
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
y
b
b
Teorema de Fermat
Seja
b
f: D ⊆R→R
b
b
uma função diferenciável num ponto a interior a D. Se f (a) é um
extremo local de f , então
f ′ (a) = 0.
b
x0
x1
x2
x3
x4
x5
x
Os pontos x0 , x2 e x4 são pontos onde a função tem mínimos locais,
enquanto que a função tem máximos locais nos pontos x1 , x3 e x5 .
A figura sugere que nos pontos x1 , x2 , x3 , x4 a derivada da função é
nula.
António Bento (UBI)
Cálculo I
2010/2011
277 / 590
António Bento (UBI)
§3.4 Aplicações do cálculo diferencial
Cálculo I
2010/2011
279 / 590
§3.4 Aplicações do cálculo diferencial
y
b
A condição
f ′ (a) = 0
b
b
b
x0
não é suficiente para a existência de extremo. Por exemplo a função
b
f : R → R,
b
x1
x2
x3
x4
x5
definida por
x
f (x) = x3 ,
Para a função representada na figura anterior vê-se facilmente que nos
pontos x0 , x2 e x4 a função tem mínimos locais e que nos pontos x1 , x3
e x5 a função tem máximos locais. Além disso, em qualquer a ∈ ]x2 , x3 [
a função tem um máximo e um mínimo local.
António Bento (UBI)
Cálculo I
2010/2011
278 / 590
tem derivada nula no ponto x = 0, mas f (0) não é extremo local.
António Bento (UBI)
Cálculo I
2010/2011
280 / 590
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
Exemplo
Sejam I um intervalo de R e
Uma bateria de voltagem fixa V e resistência interna fixa r está ligada
a um circuito de resistência variável R. Pela lei de Ohm, a corrente I
no circuito é
V
I=
.
R+r
f :I→R
uma função m vezes diferenciável, m > 1, num ponto a interior ao
intervalo I. Suponhamos que
′
f (a) = · · · = f
(m−1)
(a) = 0
e
f
(m)
Se a potência resultante é dada por P = I 2 R, mostre que a potência
máxima ocorre se R = r.
(a) 6= 0.
Então
i) se m é ímpar, f não tem qualquer extremo local no ponto a;
ii) se m é par, f tem em a um ponto de máximo local ou um ponto de
mínimo local, consoante
f (m) (a) < 0 ou
António Bento (UBI)
2
V
V 2R
De P =
temos P =
R=
. Assim, o que temos
R+r
(R + r)2
de fazer é calcular os extremos locais da função
I 2 R,
P (R) =
f (m) (a) > 0.
Cálculo I
2010/2011
281 / 590
António Bento (UBI)
§3.4 Aplicações do cálculo diferencial
V 2R
.
(R + r)2
Cálculo I
2010/2011
283 / 590
2010/2011
284 / 590
§3.4 Aplicações do cálculo diferencial
Exemplo (continuação)
Derivando a função P (R) =
Sejam I um intervalo de R e
V 2R
temos
(R + r)2
V 2 (R + r)2 − 2 (R + r) V 2 R
(R + r)4
V 2 (R + r) − 2V 2 R
=
(R + r)3
V 2r − V 2R
=
(R + r)3
V 2 (r − R)
=
(R + r)3
f :I→R
P ′ (R) =
uma função duas vezes diferenciável num ponto a interior a I com
f ′ (a) = 0.
Então
i) se f ′′ (a) > 0, a é um ponto de mínimo local;
ii) se f ′′ (a) < 0, a é um ponto de máximo local.
e, portanto,
P ′ (R) = 0 ⇔ R = r.
António Bento (UBI)
Cálculo I
2010/2011
282 / 590
António Bento (UBI)
Cálculo I
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
Exemplo (continuação)
b
Para verificarmos que R = r é um ponto de máximo local, atendendo a
que
V 2 (r − R)
P ′ (R) =
,
(R + r)3
(a, f (a))
(b, f (b))
b
função côncava
podemos fazer o seguinte quadro
R
A função f diz-se côncava ou que tem a concavidade voltada para
baixo em I se para quaisquer a, b ∈ I, com a < b, o gráfico de f em
[a, b] está acima da secante que une os ponto (a, f (a)) e (b, f (b)), isto é,
r
P ′ (R)
+
0
P (R)
−
ր
M
ց
f (x) > f (a) +
f (b) − f (a)
(x − a)
b−a
para qualquer x ∈ [a, b].
António Bento (UBI)
Cálculo I
2010/2011
285 / 590
António Bento (UBI)
§3.4 Aplicações do cálculo diferencial
b
(a, f (a))
A função f é convexa em I se para cada a, b ∈ I e para cada t ∈ [0, 1],
Sejam I um intervalo de R e f : I → R uma função. Dizemos que f é
convexa ou que tem a concavidade voltada para cima em I se
para quaisquer a, b ∈ I, com a < b, o gráfico de f em [a, b] está abaixo
da secante que une os ponto (a, f (a)) e (b, f (b)), isto é,
António Bento (UBI)
f ((1 − t)a + tb) 6 (1 − t)f (a) + tf (b).
A função f diz-se côncava em I se, para cada a, b ∈ I e para cada
t ∈ [0, 1],
f ((1 − t)a + tb) > (1 − t)f (a) + tf (b).
Obviamente, uma função f é côncava se e só se −f é convexa.
f (b) − f (a)
(x − a)
b−a
Cálculo I
287 / 590
Fazendo x = (1 − t)a + tb, t ∈ [0, 1], nas desigualdades que caracterizam
as definições de função convexa e de função côncava temos as seguintes
definições alternativas:
(b, f (b))
função convexa
para qualquer x ∈ [a, b].
2010/2011
§3.4 Aplicações do cálculo diferencial
b
f (x) 6 f (a) +
Cálculo I
2010/2011
286 / 590
António Bento (UBI)
Cálculo I
2010/2011
288 / 590
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
Sejam I um intervalo de R e f : I → R uma função diferenciável.
Então as seguintes afirmações são equivalentes:
Sejam I um intervalo de R e f : I → R uma função diferenciável.
Então as seguintes afirmações são equivalentes:
a) f é convexa;
a) f é côncava;
b) a derivada de f é monótona crescente;
b) a derivada de f é monótona decrescente;
c) para quaisquer a, x ∈ I temos
c) para quaisquer a, x ∈ I temos
f (x) > f (a) + f ′ (a) (x − a) ,
f (x) 6 f (a) + f ′ (a) (x − a) ,
ou seja, o gráfico de f está acima das suas rectas tangentes.
António Bento (UBI)
Cálculo I
2010/2011
ou seja, o gráfico de f está abaixo das suas rectas tangentes.
289 / 590
António Bento (UBI)
§3.4 Aplicações do cálculo diferencial
Cálculo I
2010/2011
291 / 590
2010/2011
292 / 590
§3.4 Aplicações do cálculo diferencial
b
b
b
b
b
b
Função convexa
António Bento (UBI)
Cálculo I
Função côncava
2010/2011
290 / 590
António Bento (UBI)
Cálculo I
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
Sejam I um intervalo de R e f : I → R uma função duas vezes
diferenciável em I. Então
Sejam I um intervalo de R e
a) f é convexa em I se e só se
f :I→R
f ′′ (x) > 0
uma função duas vezes diferenciável. Se a ∈ I é um ponto de inflexão
de f , então
f ′′ (a) = 0.
para qualquer x ∈ I;
b) f é côncava em I se e só se
f ′′ (x) 6 0
para qualquer x ∈ I.
António Bento (UBI)
Cálculo I
2010/2011
293 / 590
António Bento (UBI)
Cálculo I
2010/2011
295 / 590
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
Sejam I um intervalo, a um ponto interior a I e f : I → R. Diz-se que
a é um ponto de inflexão de f se existe ε > 0 tal que num dos
conjuntos ]a − ε, a[ ou ]a, a + ε[ a função é convexa e no outro é côncava.
Assim, podemos usar a informação que as derivadas nos fornecem para
fazer o esboço do gráfico de uma função. Para tal devemos estudar
y
• o domínio da função;
• os zeros da função;
• a continuidade da função;
• a paridade da função;
b
b
b
• os intervalos de monotonia da função;
• os extremos relativos da função;
a0
a1
a2
• as concavidades da função;
x
• os pontos de inflexão da função;
Na figura anterior vemos que a função f é côncava à esquerda de a1 e é
convexa à direita de a1 . Logo a1 é um ponto de inflexão.
António Bento (UBI)
Cálculo I
2010/2011
294 / 590
• as assímptotas da função.
António Bento (UBI)
Cálculo I
2010/2011
296 / 590
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
Exemplo – estudo da função f (x) = x2 /(x − 1) (continuação)
Exemplo – estudo da função f (x) = x2 /(x − 1)
Calculemos os zeros da primeira derivada
Seja f a função real de variável real definida por
f (x) =
f ′ (x) = 0 ⇔
x2
.
x−1
Vamos fazer um estudo completo desta função. Esta função tem como
domínio a seguinte função
Df = {x ∈ R : x − 1 6= 0} = R \ {1}
⇔ x(x − 2) = 0 ∧ (x − 1)2 6= 0
⇔ (x = 0 ∨ x = 2) ∧ x 6= 1.
Atendendo a que o denominador de f ′ é sempre positivo, temos o
seguinte quadro de sinal
e como
x2
f (x) = 0 ⇔
= 0 ⇔ x = 0 ∧ x 6= 1,
x−1
f tem apenas um zero no ponto x = 0. Além disso, a função é contínua
pois é o quociente de duas funções polinomiais.
António Bento (UBI)
Cálculo I
2010/2011
297 / 590
0
x
+
0
f (x)
−
ր
M
ց
Obviamente, esta função não é par nem é ímpar. A função é
diferenciável em todo o domínio e primeira derivada é dada por
=
=
=
António Bento (UBI)
ND
−
0
+
ց
m
ր
Além disso, f (0) = 0 e f (2) = 4.
António Bento (UBI)
Cálculo I
2010/2011
299 / 590
Exemplo – estudo da função f (x) = x2 /(x − 1) (continuação)
A segunda derivada de f é dada por
(x2 )′ (x − 1) − x2 (x − 1)′
(x − 1)2
2x (x − 1) − x2
(x − 1)2
2x2 − 2x − x2
(x − 1)2
x2 − 2x
(x − 1)2
x(x − 2)
.
(x − 1)2
Cálculo I
ND
2
§3.4 Aplicações do cálculo diferencial
Exemplo – estudo da função f (x) = x2 /(x − 1) (continuação)
=
1
f ′ (x)
§3.4 Aplicações do cálculo diferencial
f ′ (x) =
x(x − 2)
=0
(x − 1)2
f ′′ (x) =
x2 − 2x
2
(x − 1)
!′
=
h
i′
′
2
2
x2 − 2x (x − 1) − (x − 1)
x2 − 2x
4
(x − 1)
2
2
(2x − 2) (x − 1) − 2 (x − 1) x2 − 2x
2 (x − 1) − 2 x2 − 2x
=
=
4
3
(x − 1)
(x − 1)
2
2x2 − 4x + 2 − 2x2 + 4x
=
=
3
(x − 1)
(x − 1)3
e, portanto, f não tem pontos de inflexão já que a segunda derivada não tem
zeros.
2010/2011
298 / 590
António Bento (UBI)
Cálculo I
2010/2011
300 / 590
§3.4 Aplicações do cálculo diferencial
§3.4 Aplicações do cálculo diferencial
Exemplo – estudo da função f (x) = x2 /(x − 1) (continuação)
Por outro lado, tendo em conta que o domínio de f é R \ {1} e que f é
uma função contínua, a única possibilidade para assímptota vertical ao
gráfico de f é a recta de equação x = 1. Como
Exemplo – estudo da função f (x) = x2 /(x − 1) (continuação)
Fazendo um quadro temos
1
x
f ′′ (x)
f (x)
−
∩
ND
+
ND
∪
lim f (x) = lim
x→1+
x→1+
e
o que nos permite concluir que f tem a concavidade voltada para baixo
em ] − ∞, 1[ e tem a concavidade voltada para cima em ]1, +∞[.
x2
1
= + = +∞
x−1
0
x2
1
= − = −∞,
0
x→1−
x→1− x − 1
a recta de equação x = 1 é de facto uma assímptota vertical ao gráfico
de f .
lim f (x) = lim
Estamos em condições de esboçar o gráfico de f .
António Bento (UBI)
Cálculo I
2010/2011
301 / 590
António Bento (UBI)
§3.4 Aplicações do cálculo diferencial
Cálculo I
2010/2011
303 / 590
§3.4 Aplicações do cálculo diferencial
Exemplo – estudo da função f (x) = x2 /(x − 1) (continuação)
Exemplo – estudo da função f (x) = x2 /(x − 1) (continuação)
Quanto a assímptotas, uma vez que
f (x)
x2
x2
1
= lim 2
= lim 2
= lim
=1
x→+∞ x
x→+∞ x − x
x→+∞ x (1 − 1/x)
x→+∞ 1 − 1/x
lim
4
e
x2
x2 − x2 + x
− x = lim
x→+∞ x − 1
x→+∞
x−1
x
1
= lim
= lim
=1
x→+∞ x(1 − 1/x)
x→+∞ 1 − 1/x
lim f (x) − x = lim
x→+∞
1
−1
a recta de equação y = x + 1 é uma assímptota não vertical à direita do
gráfico de f . Do mesmo modo se conclui que esta recta também é
assímptota não vertical à esquerda do gráfico de f .
António Bento (UBI)
Cálculo I
2010/2011
302 / 590
António Bento (UBI)
1
Cálculo I
2
2010/2011
304 / 590
§4.1 Primitivas imediatas
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
Primitivas imediatas
Primitivação por partes
Primitivação por substituição
Primitivas de funções racionais
Sejam I um intervalo e
f :I→R
uma função. Chama-se primitiva de f em I a toda a função
5
Cálculo integral em R
6
Sucessões e séries
António Bento (UBI)
F :I→R
tal que
F ′ (x) = f (x) para qualquer x ∈ I.
Diz-se que f é primitivável em I quando f possui pelo menos uma
primitiva.
Cálculo I
2010/2011
305 / 590
António Bento (UBI)
Cálculo I
2010/2011
307 / 590
§4.1 Primitivas imediatas
Índice
Exemplos
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
Primitivas imediatas
Primitivação por partes
Primitivação por substituição
Primitivas de funções racionais
5
Cálculo integral em R
6
Sucessões e séries
a) Uma primitiva da função f : R → R dada por
f (x) = x
é a função F : R → R definida por
F (x) =
b) Dum modo mais geral, dado n ∈ N, uma primitiva da função
f : R → R definida por
f (x) = xn
é a função F : R → R definida por
F (x) =
António Bento (UBI)
x2
.
2
Cálculo I
2010/2011
306 / 590
António Bento (UBI)
xn+1
.
n+1
Cálculo I
2010/2011
308 / 590
§4.1 Primitivas imediatas
§4.1 Primitivas imediatas
Se f e g são duas funções primitiváveis num intervalo I e k ∈ R, então
Sejam I um intervalo e
uma primitiva de uma função
F :I→R
Z
f (x) + g(x) dx =
Z
f (x) dx +
Z
g(x) dx
e
f : I → R.
Z
Então, para qualquer c ∈ R, a função
kf (x) dx = k
Z
f (x) dx.
Assim,
F +c
Z
é também uma primitiva de f .
an xn + an−1 xn−1 + · · · + a1 x + a0 dx
= an
Reciprocamente, qualquer outra primitiva de f é da forma
xn+1
xn
x2
+ an−1
+ · · · + a1 + a0 x + c.
n+1
n
2
F + c, c ∈ R.
António Bento (UBI)
Cálculo I
2010/2011
309 / 590
António Bento (UBI)
§4.1 Primitivas imediatas
Por uma questão de simplicidade de escrita escrevemos apenas
Z
f (x) dx = F (x) + c.
e de um modo mais geral
Z
António Bento (UBI)
f (x) =
F (x) =
1
0
se x > 0,
se x < 0,
(
x+c
d
se x > 0;
se x < 0;
e independentemente do valor que se dê a F (0), a função F não é
derivável em x = 0, o que contradiz o facto de F ser uma primitiva de
f.
xn+1
+ c.
n+1
Cálculo I
(
não é primitivável em R, pois se F fosse uma primitiva de f , a
restrição de F ao intervalo ]0, +∞[ seria uma função da forma x + c e a
restrição de F ao intervalo ] − ∞, 0[ seria da forma d. Assim a restrição
de F a R \ {0} seria
x2
x dx =
+c
2
xn dx =
311 / 590
Nem todas as funções são primitiváveis. Por exemplo, a função
f : R → R definida por
Tendo em conta o que vimos anteriormente, se F : I → R é uma primitiva de
f temos
Z
f (x) dx = {F (x) + c : c ∈ R} .
Z
2010/2011
§4.1 Primitivas imediatas
O conjunto das primitivas de uma função f : I → R representa-se por
Z
f (x) dx.
Assim,
Cálculo I
2010/2011
310 / 590
António Bento (UBI)
Cálculo I
2010/2011
312 / 590
§4.1 Primitivas imediatas
§4.1 Primitivas imediatas
Já sabemos que para qualquer x > 0 se tem
Z
1
(ln x) =
x
′
e se x < 0 tem-se
xα dx =
xα+1
+c
α+1
α 6= −1
(−x)
−1
1
=
= .
−x
−x
x
1
Assim, uma primitiva da função f (x) = em R \ {0} é a função ln |x|. No
x
entanto, as funções do tipo
ln |x| + c
[u(x)]α+1
+c
α+1
Z
u′ (x) [u(x)] dx =
Z
u′ (x)
dx = ln |u(x)| + c
u(x)
u′ (x) eu(x) dx = eu(x) +c
α
α 6= −1
′
′
[ln (−x)] =
1
não nos dão todas as primitivas de f (x) = . Para obtermos todas as
x
primitivas de f temos de considerar todas as funções da forma
(
ln x + c1
se x > 0;
ln (−x) + c2 se x < 0.
António Bento (UBI)
Cálculo I
2010/2011
Z
1
dx = ln |x| + c
x
Z
e dx = e +c
Z
Z
sen x dx = − cos x + c
Z
u′ (x) sen [u(x)] dx = − cos [u(x)] + c
Z
cos x dx = sen x + c
Z
u′ (x) cos [u(x)] dx = sen [u(x)] + c
313 / 590
x
x
António Bento (UBI)
§4.1 Primitivas imediatas
por
ln |x| + c,
Z
1
dx = ln |x| + c.
x
O que foi feito relativamente à função
f (x) =
1
x
será feito relativamente a todas as funções cujo domínio é a reunião de
intervalos disjuntos dois a dois.
António Bento (UBI)
Cálculo I
2010/2011
315 / 590
§4.1 Primitivas imediatas
Por uma questão de simplicidade passamos a representar todas as
funções da forma
(
ln x + c1
se x > 0;
ln (−x) + c2 se x < 0.
ou seja,
Cálculo I
2010/2011
314 / 590
Z
1
dx = tg x + c
cos2 x
Z
u′ (x)
dx = tg [u(x)] + c
cos2 [u(x)]
Z
1
dx = − cotg x + c
sen2 x
Z
u′ (x)
dx = − cotg [u(x)] + c
sen2 [u(x)]
Z
senh x dx = cosh x + c
Z
u′ (x) senh [u(x)] dx = cosh [u(x)]+c
Z
cosh x dx = senh x + c
Z
u′ (x) cosh [u(x)] dx = senh [u(x)]+c
Z
1
√
dx = arc sen x + c
1 − x2
Z
Z
1
dx = arc tg x + c
1 + x2
u′ (x)
q
dx = arc sen [u(x)] + c
2
1 − [u(x)]
Z
António Bento (UBI)
Cálculo I
u′ (x)
1 + [u(x)]2
dx = arc tg [u(x)] + c
2010/2011
316 / 590
§4.2 Primitivação por partes
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
Primitivas imediatas
Primitivação por partes
Primitivação por substituição
Primitivas de funções racionais
5
Cálculo integral em R
6
Sucessões e séries
Exemplos de primitivação por partes
Z
a) Calculemos por partes x sen x dx:
Z
Z
x2
x sen x dx =
sen x −
2
Z
x2
=
sen x −
2
x2
′
(sen x) dx
2
x2
cos x dx.
2
A primitiva que agora temos de calcular é mais complicada do que a
inicial. No entanto, trocando os papeis das funções temos
Z
Z
x sen x dx = (− cos x) x − (− cos x) x′ dx
Z
= −x cos x − (− cos x) dx
Z
= −x cos x + cos x dx
= −x cos x + sen x + c.
António Bento (UBI)
Cálculo I
2010/2011
317 / 590
António Bento (UBI)
Cálculo I
§4.2 Primitivação por partes
2010/2011
319 / 590
§4.2 Primitivação por partes
Sejam I um intervalo e
f, g : I → R
Exemplos de primitivação por partes (continuação)
duas funções diferenciáveis em I. Como
b) Para primitivarmos a função ln x temos de primitivar por partes:
[f (x) g(x)]′ = f ′ (x) g(x) + f (x) g′ (x)
tem-se
Z
f ′ (x) g(x) = [f (x) g(x)]′ − f (x) g′ (x).
Assim, f ′ g é primitivável se e só se f g′ o é e
Z
′
f (x) g(x) dx =
Z
′
[f (x) g(x)] dx −
Z
′
f (x) g (x) dx,
ou seja,
Z
f ′ (x) g(x) dx = f (x) g(x) −
Z
ln x dx =
Z
1 . ln x dx
= x ln x −
Z
x (ln x)′ dx
= x ln x −
Z
x
= x ln x −
Z
1 dx
1
dx
x
= x ln x − x + c
f (x) g′ (x) dx
que é a fórmula de primitivação por partes.
António Bento (UBI)
Cálculo I
2010/2011
318 / 590
António Bento (UBI)
Cálculo I
2010/2011
320 / 590
§4.2 Primitivação por partes
§4.2 Primitivação por partes
Exemplos de primitivação por partes (continuação)
Exemplos de primitivação por partes (continuação)
c) Vejamos como primitivar a função arc tg x:
e) Primitivando por partes a função sen2 x temos
Z
arc tg x dx =
Z
1. arc tg x dx
= x arc tg x −
=
=
=
=
António Bento (UBI)
Z
Z
2
sen x dx =
x (arc tg x)′ dx
1
dx
x arc tg x − x
1 + x2
Z
x
x arc tg x −
dx
1 + x2
Z
1
2x
x arc tg x −
dx
2 1 + x2
1 x arc tg x − ln 1 + x2 + c
2
Z
Cálculo I
2010/2011
321 / 590
Z
António Bento (UBI)
Z
tem-se
= x arc sen x −
Z
1
x√
dx
1 − x2
o que implica
= x arc sen x −
Z
√
e, portanto,
= x arc sen x +
Z
−2x
√
dx
2 1 − x2
= x arc sen x +
Cálculo I
= − cos x sen x −
Z
− cos x cos x dx
= − sen x cos x +
Z
cos2 x dx
= − sen x cos x +
Z
1 − sen2 x dx
Z
sen2 x dx.
Cálculo I
e) (continuação) Fazendo I =
x (arc sen x)′ dx
p
− cos x (sen x)′ dx
António Bento (UBI)
1 . arc sen x dx
= x arc sen x −
Z
2010/2011
323 / 590
Exemplos de primitivação por partes (continuação)
d) A primitiva de arc sen x calcula-se de forma semelhante:
arc sen x dx =
= − cos x sen x −
§4.2 Primitivação por partes
Exemplos de primitivação por partes (continuação)
Z
sen x sen x dx
= − sen x cos x + x −
§4.2 Primitivação por partes
Z
Z
x
dx
1 − x2
Assim,
António Bento (UBI)
Z
sen2 x dx
I = − sen x cos x + x − I
2I = − sen x cos x + x
I=−
322 / 590
sen2 x dx em
sen2 x dx = − sen x cos x + x −
1 − x2 + c
2010/2011
Z
Z
sen x cos x x
+ .
2
2
sen2 x dx = −
sen x cos x x
+ + c.
2
2
Cálculo I
2010/2011
324 / 590
§4.2 Primitivação por partes
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
ex (sen x)′ dx
3
Cálculo diferencial em R
ex cos x dx
4
Primitivas
Primitivas imediatas
Primitivação por partes
Primitivação por substituição
Primitivas de funções racionais
ex (− sen x) dx
5
Cálculo integral em R
ex sen x dx
6
Sucessões e séries
Exemplos de primitivação por partes (continuação)
f ) Primitivemos por partes a função ex sen x:
Z
ex sen x dx = ex sen x −
= ex sen x −
Z
Z
= ex sen x − ex cos x −
= ex sen x − ex cos x +
= ex sen x − ex cos x −
António Bento (UBI)
Z
Z
Z
ex (cos x)′ dx
Cálculo I
2010/2011
325 / 590
António Bento (UBI)
§4.2 Primitivação por partes
Z
(F ◦ ϕ)′ (t) = F ′ (ϕ(t)) ϕ′ (t) = f (ϕ(t)) ϕ′ (t)
ex sen x dx
F ◦ ϕ é uma primitiva de (f ◦ ϕ) ϕ′ . Assim, para calcularmos as
primitivas de f (x) basta calcularmos as primitivas de f (ϕ(t)) ϕ′ (t) e
depois fazer a mudança de variável t = ϕ−1 (x), ou seja,
concluímos que
2
Z
ex sen x dx = ex sen x − ex cos x
Z
e, portanto,
Z
António Bento (UBI)
ex sen x dx =
f (x) dx =
Z
f (ϕ(t)) ϕ (t) dt t=ϕ−1 (x) .
′
Para primitivarmos por substituição usamos a notação
ex
(sen x − cos x) + c.
2
Cálculo I
327 / 590
Sejam I e J dois intervalos de R, f : I → R uma função primitivável e
ϕ : J → I uma função bijectiva e diferenciável e tal que ϕ′ (t) 6= 0 para
cada t ∈ J. Suponhamos que F : I → R é uma primitiva de f . Como
f ) (continuação) De
ex sen x dx = ex sen x − ex cos x −
2010/2011
§4.3 Primitivação por substituição
Exemplos de primitivação por partes (continuação)
Z
Cálculo I
dx = ϕ′ (t)dt.
2010/2011
326 / 590
António Bento (UBI)
Cálculo I
2010/2011
328 / 590
§4.3 Primitivação por substituição
§4.3 Primitivação por substituição
Exemplos de primitivação por substituição
Z p
a) Para calcularmos
a2 − x2 dx, a > 0, fazemos a substituição
Exemplos de primitivação por substituição (continuação)
a) (continuação) Assim,
Z p
a2
x = a sen t
e, portanto,
dx = (a sen t) dt = a cos t dt
−
2
=a
x2 dx
= a2
′
e atendendo a que
o que dá
Cálculo I
2010/2011
cos2 t dt
sen t cos t
t
+ a2 + c
2
2
x = a sen t,
Z p
Z p
a2 − x2 dx =
a2 − a2 sen2 t a cos t dt
Z p
=
a2 (1 − sen2 t) a cos t dt
Z √
a2 cos2 t a cos t dt
=
Z
=
a cos t a cos t dt
Z
= a2 cos2 t dt.
António Bento (UBI)
Z
resulta
t = arc sen
x
a
o que dá
Z p
a2
329 / 590
−
x2 dx
x
ax
x
a2
cos arc sen
arc sen + c
=
+
2
a
2
a
2
x p 2
a
x
=
a − x2 +
arc sen + c
2
2
a
António Bento (UBI)
§4.3 Primitivação por substituição
Cálculo I
2010/2011
331 / 590
§4.3 Primitivação por substituição
Exemplos de primitivação por substituição (continuação)
a) (continuação) Primitivando por partes
Z
cos2 t dt =
Z
= sen t cos t −
Z
2
o que implica
Z
Z
Exemplos de primitivação por substituição (continuação)
b) Para calcularmos a primitiva
Z
Z
sen t (− sen t) dt
1 − cos2 t dt
= sen t cos t + t −
e, portanto,
cos2 t dt temos
cos t cos t dt
= sen t cos t +
António Bento (UBI)
Z
Z
x2
√
1
dx
1 − x2
fazemos a substituição
x = sen t
cos2 t dt
o que dá
cos2 t dt = sen t cos t + t
dx = (sen t)′ dt
= cos t dt.
cos2 t dt =
sen t cos t
t
+ +c
2
2
Cálculo I
2010/2011
330 / 590
António Bento (UBI)
Cálculo I
2010/2011
332 / 590
§4.3 Primitivação por substituição
§4.3 Primitivação por substituição
Exemplos de primitivação por substituição (continuação)
Exemplos de primitivação por substituição (continuação)
b) (continuação) Assim,
d) Calculemos
Z
1
√
dx =
2
x 1 − x2
Z
=
Z
=
Z
1
√
cos t dt
2
sen t 1 − sen2 t
usando a substituição
1
cos t dt
2
sen t cos t
dx = (2 tg t)′ dt =
p
x2 + 4 =
2010/2011
333 / 590
c) Se quisermos calcular a primitiva
Z
1
√
dx
(1 + x2 ) 1 + x2
=
1
1+
p
tg2 t
Z
x2
√
Z
=
1
4
1
dt
cos2 t
1
dt
cos2 t
=−
=−
x
= sen (arc tg x) + c = √
+c
1 + x2
António Bento (UBI)
Cálculo I
r
+1 =2
1
2
=
2
cos t
cos t
Cálculo I
1
dx =
x2 + 4
1
1
2
2
Z cos t cos t
= cos t dt = sen t + c
r
4
tg2 t
4 tg2 t + 4
2010/2011
335 / 590
Exemplos de primitivação por substituição (continuação)
1
dt, o que dá
cos2 t
1
1
q
q
d) (continuação) Assim,
fazemos a substituição x = tg t e, portanto, dx =
Z
(2 tg t)2 + 4 =
§4.3 Primitivação por substituição
Exemplos de primitivação por substituição (continuação)
+ tg2 t
=
q
António Bento (UBI)
§4.3 Primitivação por substituição
Z
2
dt.
cos2 t
Além disso,
Cálculo I
1
√
dx =
2
(1 + x ) 1 + x2
1
dx,
x2 + 4
Então
1
dt
sen2 t
= − cotg(arc sen x) + c
√
1 − x2
=−
+c
x
Z
x2
√
x = 2 tg t.
= − cotg t + c
António Bento (UBI)
Z
2010/2011
334 / 590
António Bento (UBI)
1
2
4 tg2 t
cos t
Z
2
1
dt =
cos2 t
4
cos t sen−2 t dt =
Z
1
1
dt
sen2 t cos t
cos2 t
1 sen−1 t
+c
4 −1
1
1
+c=−
+c
4 sen t
4 sen (arc tg x/2)
√
x2 + 4
+c
4x
Cálculo I
2010/2011
336 / 590
§4.3 Primitivação por substituição
Índice
Exemplos de primitivação por substituição (continuação)
e) Calculemos a seguinte primitiva
fazendo a substituição
Z
x2
√
1
dx,
x2 − 1
x = sec t =
1
cos t
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
Primitivas imediatas
Primitivação por partes
Primitivação por substituição
Primitivas de funções racionais
5
Cálculo integral em R
6
Sucessões e séries
e, portanto,
dx =
Além disso,
p
x2 − 1 =
António Bento (UBI)
1
cos t
r
′
dt =
sen t
dt.
cos2 t
1
−1=
cos2 t
q
tg2 t = tg t.
Cálculo I
2010/2011
337 / 590
António Bento (UBI)
§4.3 Primitivação por substituição
f (x) =
1
√
dx =
2
x x2 − 1
Z
1
sen t
dt
1
cos2 t
tg
t
cos2 t
=
Z
cos t dt
António Bento (UBI)
Cálculo I
e, portanto,
P (x)
Q(x)
onde P e Q são polinómios e D = {x ∈ R : Q(x) 6= 0}. Assumimos que
P e Q não têm zeros (reais ou complexos) comuns. Se o grau de P é
maior ou igual do que o grau de Q, então fazendo a divisão de P por Q
temos
P (x) = D(x)Q(x) + R(x)
= sen t + c
1
= sen arc cos
x
√
x2 − 1
=
+c
x
339 / 590
Uma função racional é uma função f : D → R definida por
e) (continuação) Assim,
2010/2011
§4.4 Primitivas de funções racionais
Exemplos de primitivação por substituição (continuação)
Z
Cálculo I
+c
P (x)
R(x)
= D(x) +
Q(x)
Q(x)
onde D e R são polinómios e o grau de R é menor do que o grau de Q.
Assim, para primitivarmos as funções racionais basta sabermos
primitivar as funções racionais onde o grau do numerador é menor do
que o grau do denominador.
2010/2011
338 / 590
António Bento (UBI)
Cálculo I
2010/2011
340 / 590
§4.4 Primitivas de funções racionais
§4.4 Primitivas de funções racionais
Sejam P e Q dois polinómios com o grau de P menor do que o grau de
Q e sem zeros (reais ou complexos) em comum. Então
n1
Q(x) = (x − a1 )
. . . (x − ak )
onde os zeros reais de Q são
a1 , . . . , ak
nk
h
im1
h
iml
2
2
(x − α1 ) + β12
. . . (x − αl ) + βl2
com multiplicidades
Exemplos de primitivação de funções racionais
a) Calculemos
Z
Fazendo a divisão de x2 por x2 − 1 temos
x2 +0x +0 | x2 +0x −1
n1 , . . . , nk ,
−x2 −0x +1
respectivamente, e os zeros complexos de Q são
α1 + β1 i, . . . , αl + βl i
com multiplicidades
com multiplicidades
e, portanto,
x2
1
=1+ 2
.
2
x −1
x −1
Agora precisamos de factorizar o denominador. Para isso basta ter
em conta que zeros do denominador que são 1 e −1.
m 1 , . . . , ml ,
respectivamente.
António Bento (UBI)
Cálculo I
2010/2011
341 / 590
António Bento (UBI)
§4.4 Primitivas de funções racionais
x2
António Bento (UBI)
x2
pelo que
Fazendo x = −1 resulta que B = − 1/2 e fazendo x = 1 tem-se
A = 1/2, ou seja,
i
2010/2011
1
A(x + 1) + B(x − 1)
=
,
−1
(x − 1) (x + 1)
A(x + 1) + B(x − 1) = 1.
m
Cálculo I
1
1
A
B
=
=
+
−1
(x − 1)(x + 1)
x−1 x+1
e, portanto,
k X
l X
i
l
X
Ai,j
Bi,j x + Ci,j
P (x) X
=
+
h
ij .
j
2
Q(x) i=1 j=1 (x − ai )
i=1 j=1 (x − α ) + β 2
i
343 / 590
a) (continuação) Então existem números reais A e B tais que
Bl,1 x + Cl,1
Bl,m1 x + Cl,ml
iml ,
+ ··· + h
2
2
(x − αl ) + βl
(x − αl )2 + βl2
n
2010/2011
Exemplos de primitivação de funções racionais (continuação)
P (x)
A1,1
A1,n1
=
+ ··· +
+
Q(x)
x − a1
(x − a1 )n1
Ak,1
Ak,nk
+ ··· +
+
+··· +
x − ak
(x − ak )nk
B1,1 x + C1,1
B1,m1 x + C1,m1
im1 +
+
+ ··· + h
2
2
(x − α1 ) + β1
(x − α1 )2 + β12
ou seja,
Cálculo I
§4.4 Primitivas de funções racionais
Além disso, existem números reais A′ s, B ′ s e C ′ s tais que
+··· +
1
+0x +1
m 1 , . . . , ml ,
respectivamente, e
α1 − β1 i, . . . , αl − βl i
x2
dx.
x2 − 1
x2
342 / 590
António Bento (UBI)
1
1/2
1/2
=
−
.
−1
x−1 x+1
Cálculo I
2010/2011
344 / 590
§4.4 Primitivas de funções racionais
§4.4 Primitivas de funções racionais
Exemplos de primitivação de funções racionais (continuação)
Exemplos de primitivação de funções racionais (continuação)
b) (continuação) Fazendo x = 0 em
A x2 + 1 + Bx x2 + 1 + Cx2 x2 + 1 + (Dx + E) x3 = x + 1.
a) (continuação) Assim,
Z
temos A = 1 e fazendo x = i tem-se
x2
dx =
x2 − 1
Z
1+
=
Z
−1/2
1/2
+
dx
1+
x−1 x+1
Z
1 dx +
=
1
dx
2
x −1
1
2
Z
(Di + E) i3 = i + 1 ⇔ (Di + E) (−i) = 1 + i ⇔ D − Ei = 1 + i
1
1
dx −
x−1
2
o que implica D = 1 e E = −1. Fazendo x = 1 obtemos
2A + 2B + 2C + D + E = 2 ⇔ 2 + 2B + 2C + 1 − 1 = 2 ⇔ B + C = 0
Z
e fazendo x = −1 resulta
1
dx
x+1
2A − 2B + 2C + D − E = 0 ⇔ 2 − 2B + 2C + 1 − (−1) = 0
⇔ −2B + 2C = −4
1
1
= x + ln |x − 1| − ln |x + 1| + c.
2
2
António Bento (UBI)
Cálculo I
2010/2011
o que dá o sistema
B+C =0
−B + C = −2
345 / 590
António Bento (UBI)
§4.4 Primitivas de funções racionais
⇔ −B + C = −2,
⇔
B = −C
C + C = −2
⇔
B=1
C = −1
Cálculo I
2010/2011
§4.4 Primitivas de funções racionais
Exemplos de primitivação de funções racionais (continuação)
Exemplos de primitivação de funções racionais (continuação)
b) Consideremos a função f definida por
x+1
f (x) = 3 2
.
x (x + 1)
b) (continuação) Assim,
1
1
x+1
1
x−1
= 3+ 2− + 2
x3 (x2 + 1)
x
x
x x +1
pelo que
Então temos de ter
f (x) =
x+1
A
B
C
Dx + E
= 3+ 2+ + 2
x3 (x2 + 1)
x
x
x
x +1
A x2 + 1 + Bx x2 + 1 + Cx2 x2 + 1 + (Dx + E) x3
x+1
= 3 2
,
3
2
x (x + 1)
x (x + 1)
o que implica
A x2 + 1 + Bx x2 + 1 + Cx2 x2 + 1 + (Dx + E) x3 = x + 1.
António Bento (UBI)
Cálculo I
2010/2011
x+1
dx
+ 1)
Z
Z
Z
Z
1
1
1
x−1
=
dx
+
dx
−
dx
+
dx
3
2
x
x
x
xZ2 + 1
Z
Z
Z
Z
1
1
2x
1
−3
−2
= x dx + x dx −
dx +
dx −
dx
2
2
x
2 x +1
x +1
x−2 x−1
1 =
+
− ln |x| + ln x2 + 1 − arc tg x + c
−2
−1
2
1
1 2
1
= − 2 − − ln |x| + ln x + 1 − arc tg x + c
2x
x
2
Z
e, portanto,
347 / 590
346 / 590
x3 (x2
António Bento (UBI)
Cálculo I
2010/2011
348 / 590
§4.4 Primitivas de funções racionais
§4.4 Primitivas de funções racionais
Para as funções do tipo
Tendo em conta a decomposição que obtivemos, para primitivarmos
funções racionais basta sabermos calcular as seguintes primitivas
Z
e
Z
A
(x − a)k
Bx + C
h
(x − α)2 + β 2
fazendo a mudança de variável x = α + βt tem-se dx = βdt e
Z
dx
Bx + C
(x − α)2 + β 2
Bx + C
dx =
(x − α)2 + β 2
=
ik dx,
Z
Z
B
2
B
=
2
=
onde A, B, C, a, α ∈ R, β ∈ R \ {0} e k ∈ N.
B (α + βt) + C
β dt
β 2 t2 + β 2
βBt + αB + C
β dt
β 2 (t2 + 1)
Z
Z
2t
1
αB + C
dt
+
dt
2
2
t +1
β
t +1
αB + C
ln t2 + 1 +
arc tg t + c
β
António Bento (UBI)
Cálculo I
2010/2011
349 / 590
António Bento (UBI)
§4.4 Primitivas de funções racionais
A
(x − a)k
dx = A
Z
(x − a)−k dx
(x − a)−k+1
+c
−k + 1
A
1
=−
+ c.
k − 1 (x − a)k−1
=A
António Bento (UBI)
Cálculo I
2
Cálculo I
αB + C
x−α
+ 1 +
arc tg
+c
β
β
2010/2011
351 / 590
§4.4 Primitivas de funções racionais
A primeira primitiva é bastante simples de calcular pois quando k = 1
temos
Z
Z
A
1
dx = A
dx = A ln |x − a| + c
x−a
x−a
e quando k > 1 vem
Z
B x − α
=
ln 2 β
Usando a mesma mudança de variável x = α + βt, pelo que dx = βdt, vem
Z
Z
Bx + C
B (α + βt) + C
β dt
h
ik dx =
k
2
(β 2 t2 + β 2 )
(x − α) + β 2
Z
βBt + αB + C
=
β dt
k
β 2k (t2 + 1)
Z
Z
B
2t
αB + C
1
=
dt
+
dt
k
k
2k−1
2
2
2β 2k−2
β
(t + 1)
(t + 1)
Z
Z
−k
B
αB + C
1
2
=
2t t + 1
dt + 2k−1
dt
k
2
2β 2k−2
β
(t + 1)
−k+1
Z
t2 + 1
αB + C
1
B
=
+
dt
k
2k−2
2k−1
2
2β
−k + 1
β
(t + 1)
e, portanto, temos de saber calcular
Z
Ik =
2010/2011
350 / 590
António Bento (UBI)
1
(t2
k
+ 1)
Cálculo I
dt.
2010/2011
352 / 590
§4.4 Primitivas de funções racionais
§4.4 Primitivas de funções racionais
Para isso temos
Ik =
Z
1
dt =
2
(t + 1)k
Z
t2 + 1 − t2
dt =
(t2 + 1)k
= Ik−1 −
1
2
Z
1
= Ik−1 −
2
"
1
2
Z
1
dt −
2
(t + 1)k−1
−k
2t t2 + 1
−k+1
t2 + 1
−k + 1
Z
3) decompor a função racional (a que obtivemos na divisão ou a inical, caso
não tenha sido necessário fazer a divisão) numa soma de parcelas da forma
A1
A2
An−1
An
+
+ ···+
+
,
(x − a)n
(x − a)n−1
(x − a)2
(x − a)
por cada factor
t dt
t−
Z
−k+1
t2 + 1
−k + 1
1 dt
#
Z
1
1
t
1
−
dt
2
1 − k (t2 + 1)k−1
1−k
(t + 1)k−1
1
t
1
= Ik−1 +
+
Ik−1
2k − 2 (t2 + 1)k−1
2 − 2k
3 − 2k
1
t
Ik−1 +
=
2 − 2k
2k − 2 (t2 + 1)k−1
= Ik−1 −
Primitivação de funções racionais – resumo (continuação)
t2
dt
(t2 + 1)k
o que dá uma fórmula por recorrência para calcular primitivas do tipo
Z
António Bento (UBI)
(x − a)n , n ∈ N
que aparece na factorização de Q(x), e da forma
B1 x + C1
B2 x + C2
Bm−1 x + Cm−1
Bm x + Cm
+
,
+·· ·+
+
2
2
2
[(x − α)2 + β 2 ]m [(x − α)2 + β 2 ]m−1
(x
− α)2 + β 2
[(x − α) + β ]
por cada factor
m
(x − α)2 + β 2 , m ∈ N
que aparece na factorização de Q(x) e onde cada Ak , cada Bk e cada Ck é
um número real;
1
dt.
2
(t + 1)k
4) primitivar cada uma das parcelas obtidas na decomposição.
Cálculo I
2010/2011
353 / 590
António Bento (UBI)
§4.4 Primitivas de funções racionais
Cálculo I
Exemplo de primitivação de uma função racional
P (x)
, com P e Q polinómios sem
Q(x)
zeros (reais ou complexos) comuns, devemos fazer o seguinte:
Calculemos a primitiva Z
Para primitivarmos uma função racional
1) se o grau de P é maior ou igual do que o grau de Q, fazemos a divisão de
P (x)
P por Q. Deste modo
é igual à soma de um polinómio com uma
Q(x)
função racional em que o grau do numerador é menor do que o grau do
denominador;
ou
(x − α) + β
Cálculo I
3x5 + 3x4 + 6x3 + 6x2 + x + 2
A
B
Cx + D
Ex + F
= 2 +
+ 2
+ 2
.
x2 (x2 + 1)2
x
x
(x + 1)2
x +1
Assim, temos
A(x2 + 1)2 + Bx(x2 + 1)2 + (Cx + D)x2 + (Ex + F )x2 (x2 + 1)
A(x4 + 2x2 + 1) + B(x5 + 2x3 + x) + Cx3 + Dx2 + E(x5 + x3 ) + F (x4 + x2 )
= 3x5 + 3x4 + 6x3 + 6x2 + x + 2
e, portanto,
,
(B + E)x5 + (A + F )x4 + (2B + C + E)x3 + (2A + D + F )x2 + Bx + A
com n, m ∈ N;
António Bento (UBI)
Pelo que vimos anteriormente temos de fazer a seguinte decomposição
donde
(x − α)2 + β 2 ,
agrupando os factores repetidos de modo que fiquemos com factores
diferentes da forma
n
2
2 m
(x − a)
3x5 + 3x4 + 6x3 + 6x2 + x + 2
dx.
x2 (x2 + 1)2
= 3x5 + 3x4 + 6x3 + 6x2 + x + 2
2) factorizar Q(x) como o produto de factores da forma
ou
355 / 590
§4.4 Primitivas de funções racionais
Primitivação de funções racionais – resumo
x−a
2010/2011
2010/2011
= 3x5 + 3x4 + 6x3 + 6x2 + x + 2.
354 / 590
António Bento (UBI)
Cálculo I
2010/2011
356 / 590
§4.4 Primitivas de funções racionais
§4.4 Primitivas de funções racionais
Exemplo de primitivação de uma função racional (continuação)
Assim, de
(B + E)x5 + (A + F )x4 + (2B + C + E)x3 + (2A + D + F )x2 + Bx + A
= 3x5 + 3x4 + 6x3 + 6x2 + x + 2
resulta

B+E =3





A+F = 3


2B + C + E = 6

2A + D + F = 6




B=1



⇔
A=2
pelo que

E=2





F =1


C = 2

D=1




B=1



A=2
3x5 + 3x4 + 6x3 + 6x2 + x + 2
2
1
2x + 1
2x + 1
= 2 + + 2
+ 2
.
x2 (x2 + 1)2
x
x
(x + 1)2
x +1
António Bento (UBI)
Cálculo I
2010/2011
357 / 590
Exemplo de primitivação de uma função racional (continuação)
Z 2
Z
x + 1 − x2
1
dx =
2
2 dx
(x2 + 1)
(x2 + 1)
Z
Z
x2
x2 + 1
dx
−
=
2
2 dx
(x2 + 1)
(x2 + 1)
Z
Z
−2
1
1
=
dx
−
2x x2 + 1
x dx
2
x +1
2
"
#
−1
−1
Z
x2 + 1
1 x2 + 1
= arc tg x −
x−
1 dx
2
−1
−1
Z
1
x
1
= arc tg x −
− 2
+
dx
2
x +1
x2 + 1
1
x
1
= arc tg x +
− arc tg x + c
2
2 x +1 2
1
x
1
= arc tg x +
+c
2
2 x2 + 1
António Bento (UBI)
§4.4 Primitivas de funções racionais
Cálculo I
2010/2011
359 / 590
§4.4 Primitivas de funções racionais
Exemplo de primitivação de uma função racional (continuação)
Exemplo de primitivação de uma função racional (continuação)
Deste modo
Z
3x5 + 3x4 + 6x3 + 6x2 + x + 2
dx
x2 (x2 + 1)2
Tendo em conta que
=
Z
=2
2
1
2x + 1
2x + 1
+ + 2
+ 2
dx
x2
x
(x + 1)2
x +1
Z
+
=2
Z
x−2 dx +
Z
Z
1
dx +
x
2x
dx +
x2 + 1
Z
Z
2x(x2 + 1)−2 dx +
1
dx
x2 + 1
x−1
(x2 + 1)−1
+ ln |x| +
+
−1
−1
Z
Z
Z
(x2
António Bento (UBI)
3x5 + 3x4 + 6x3 + 6x2 + x + 2
dx
x2 (x2 + 1)2
Z
2
1
1
+
dx + ln |x2 + 1| + arc tg x
= − + ln |x| − 2
x
x +1
(x2 + 1)2
Z
1
dx + ln |x2 + 1| + arc tg x
(x2 + 1)2
Cálculo I
2010/2011
1
1
1
x
2 dx = 2 arc tg x + 2 x2 + 1 + c,
+ 1)
tem-se
1
dx
+ 1)2
2
1
1
+ ln |x| − 2
+
dx + ln |x2 + 1| + arc tg x.
x
x +1
(x2 + 1)2
Falta calcular
Z
1
dx.
(x2 + 1)2
=−
(x2
358 / 590
=−
2
1
1
1
x
+ ln |x| − 2
+ arc tg x +
+ ln |x2 + 1| + arc tg x + c
x
x +1 2
2 x2 + 1
=−
2
1
1
x
3
+ ln |x| − 2
+
+ ln |x2 + 1| + arc tg x + c
x
x + 1 2 x2 + 1
2
António Bento (UBI)
Cálculo I
2010/2011
360 / 590
§4.4 Primitivas de funções racionais
Índice
Exemplo de primitivação de uma função racional (continuação)
Z
1
dx de outro
Fazendo a substituição x = tg t, podemos calcular
2
(x + 1)2
1
modo. Assim, tendo em conta que dx =
dt, temos
cos2 t
Z
Z
Z
1
1
1
1
1
dx =
dt =
dt
2
2
2
2
2t
2
(x2 + 1)2
cos
t
(1/
cos
t)
cos
(tg t + 1)
Z
Z
Z
Z
cos(2t) + 1
1
1
=
cos2 t dt =
dt =
2 cos(2t) dt +
1 dt
2
4
2
=
t
sen t cos t
t
1
sen(2t) + + c =
+ +c
4
2
2
2
=
sen(arc tg x) cos(arc tg x) arc tg x
+
+c
2
2
=
1 x
1
+ arc tg x + c
2
2 x +1 2
António Bento (UBI)
Cálculo I
2010/2011
361 / 590
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
Integral de Riemann: definição, propriedades e exemplos
Teorema Fundamental do Cálculo
Integração por partes e integração por substituição
Aplicações do cálculo integral
Integrais impróprios
6
Sucessões e séries
António Bento (UBI)
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
Integral de Riemann: definição, propriedades e exemplos
Teorema Fundamental do Cálculo
Integração por partes e integração por substituição
Aplicações do cálculo integral
Integrais impróprios
6
2010/2011
363 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
Índice
1
Cálculo I
Seja [a, b] um intervalo de R com mais do que um ponto, ou seja, a < b.
Chama-se partição de [a, b] a todo o subconjunto
P = {x0 , x1 , . . . , xn−1 , xn }
com
a = x0 < x1 < . . . < xn−1 < xn = b.
Sucessões e séries
António Bento (UBI)
Cálculo I
2010/2011
362 / 590
António Bento (UBI)
Cálculo I
2010/2011
364 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
§5.1 Integral de Riemann: definição, propriedades e exemplos
y
Seja
f : [a, b] → R
m7
m3
uma função limitada. Para cada partição
m2 =m4 =m8
m6
m5
P = {x0 , x1 , . . . , xn−1 , xn }
b
m1
b
de [a, b], usa-se a notação
mi = mi (f, P ) = inf {f (x) : x ∈ [xi−1 , xi ]}
a
q
x0
e
i = 1, . . . , n.
Mi = Mi (f, P ) = sup {f (x) : x ∈ [xi−1 , xi ]} ,
António Bento (UBI)
Cálculo I
x1
x2
x3 x4
x5
x6
x7
x
b
q
x8
Interpretação geométrica das somas inferiores
de uma função f : [a, b] → R
2010/2011
365 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
António Bento (UBI)
Cálculo I
2010/2011
367 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
y
Designa-se por soma inferior da função f relativa à partição P ao
número
s(f, P ) =
n
X
mi (f, P ) (xi − xi−1 ) .
n
X
Mi (f, P ) (xi − xi−1 ) .
i=1
b
b
Do mesmo modo, chamamos soma superior da função f relativa à
partição P ao número
S(f, P ) =
i=1
a
q
x0
x1
x2
x3 x4
x5
x6
x7
x
b
q
x8
Interpretação geométrica das somas superiores
de uma função f : [a, b] → R
António Bento (UBI)
Cálculo I
2010/2011
366 / 590
António Bento (UBI)
Cálculo I
2010/2011
368 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
§5.1 Integral de Riemann: definição, propriedades e exemplos
Exemplos de somas superiores e de somas inferiores
a) Consideremos a função f : [a, b] → R a função definida por f (x) = c,
c ∈ R. Dada uma partição P = {x0 , x1 , . . . , xn−1 , xn } de [a, b], temos
mi (f, P ) = c
e
Uma função f : [a, b] → R diz-se integrável à Riemann em [a, b] se e
só se existir um e um só número A tal que
Mi (f, P ) = c
e, portanto,
s(f, P ) =
n
X
mi (f, P ) (xi − xi−1 ) =
i=1
n
X
=c
i=1
e
S(f, P ) =
n
X
= c
i=1
i=1
s(f, P ) 6 A 6 S(f, P ) para qualquer partição P de [a, b].
c (xi − xi−1 )
O único número A que verifica a desigualdade anterior designa-se por
integral de Riemann de f em [a, b] e representa-se por
(xi − xi−1 ) = c (b − a)
Mi (f, P ) (xi − xi−1 ) =
i=1
n
X
n
X
n
X
i=1
Z
b
f (x) dx.
a
c (xi − xi−1 )
(xi − xi−1 ) = c (b − a).
António Bento (UBI)
Cálculo I
2010/2011
369 / 590
António Bento (UBI)
§5.1 Integral de Riemann: definição, propriedades e exemplos
Cálculo I
2010/2011
371 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
Exemplos do integral de Riemann
Exemplos de somas superiores e de somas inferiores (continuação)
b) Seja f : [0, 1] → R a função definida por
f (x) =
(
0
1
se x ∈ [0, 1] ∩ Q,
se x ∈ [0, 1] ∩ (R \ Q) .
a) Consideremos novamente a função f : [a, b] → R definida por
f (x) = c. Já vimos que para qualquer partição P de [a, b] tem-se
Assim,
s(f, P ) 6 c (b − a) 6 S(f, P ) para qualquer partição P de [a, b]
Dada uma partição P de [0, 1], atendendo a que
mi (f, P ) = 0
e
Mi (f, P ) = 1,
s(f, P ) = 0
e
S(f, P ) = 1.
s(f, P ) = c (b − a) = S(f, P ).
e
c (b − a)
temos que
é o único número real que verifica as estas desigualdades. Logo f é
integrável à Riemann em [a, b] e
Z
b
a
António Bento (UBI)
Cálculo I
2010/2011
370 / 590
António Bento (UBI)
f (x) dx = c (b − a).
Cálculo I
2010/2011
372 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
§5.1 Integral de Riemann: definição, propriedades e exemplos
Propriedades dos integrais (continuação)
Exemplos do integral de Riemann (continuação)
c) Se a, b e c são números reais tais que a < c < b e
b) Já vimos que para a função f : [0, 1] → R, definida por
f (x) =
(
0
1
f : [a, b] → R
uma função limitada, então f é integrável em [a, b] se e só se f é integrável
em [a, c] e em [c, b]. Além disso,
Z b
Z c
Z b
f (x) dx =
f (x) dx +
f (x) dx.
se x ∈ [0, 1] ∩ Q,
se x ∈ [0, 1] ∩ (R \ Q) ,
se tem
a
s(f, P ) = 0
e
S(f, P ) = 1
a
d) Se
f, g : [a, b] → R
qualquer que seja a partição P de [0, 1]. Portanto, se A ∈ [0, 1]
tem-se
0 = s(f, P ) 6 A 6 S(f, P ) = 1
são duas funções integráveis em [a, b] tais que
para qualquer partição P de [0, 1], o que mostra que f não é
integrável à Riemann em [0, 1].
então
f (x) 6 g(x) para cada x ∈ [a, b],
Z
a
António Bento (UBI)
Cálculo I
c
2010/2011
373 / 590
António Bento (UBI)
§5.1 Integral de Riemann: definição, propriedades e exemplos
b
f (x) dx 6
Z
b
g(x) dx.
a
Cálculo I
2010/2011
375 / 590
§5.1 Integral de Riemann: definição, propriedades e exemplos
Propriedades dos integrais
Sejam a e b números reais tais que a < b.
Propriedades dos integrais (continuação)
a) Se
e) Seja
f, g : [a, b] → R
são funções integráveis em [a, b], então f + g é integrável em [a, b] e
Z
b
[f (x) + g(x)] dx =
a
Z
b
f (x) dx +
a
Z
b
g(x) dx.
f : [a, b] → R
uma função integrável. Então |f | é integrável em [a, b] e
Z
Z b
b
f (x) dx 6
|f (x)| dx.
a
a
a
b) Se λ é um número real e
f : [a, b] → R
é uma função integrável em [a, b], então λ f é integrável em [a, b] e
Z
b
λ f (x) dx = λ
a
António Bento (UBI)
Cálculo I
Z
b
f ) Toda a função contínua f : [a, b] → R é integrável em [a, b].
g) Toda a função monótona f : [a, b] → R é integrável em [a, b].
f (x) dx.
a
2010/2011
374 / 590
António Bento (UBI)
Cálculo I
2010/2011
376 / 590
§5.2 Teorema Fundamental do Cálculo
Índice
Teorema Fundamental do Cálculo
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
Integral de Riemann: definição, propriedades e exemplos
Teorema Fundamental do Cálculo
Integração por partes e integração por substituição
Aplicações do cálculo integral
Integrais impróprios
6
Sejam a, b ∈ R tais que a < b e
f : [a, b] → R
uma função integrável. Então a função
F : [a, b] → R
definida por
F (x) =
Z
x
f (t) dt
a
é contínua em [a, b]. Além disso, se f é contínua num ponto c ∈ [a, b],
então F é diferenciável em c e
Sucessões e séries
F ′ (c) = f (c).
António Bento (UBI)
Cálculo I
2010/2011
377 / 590
António Bento (UBI)
§5.2 Teorema Fundamental do Cálculo
Cálculo I
2010/2011
379 / 590
§5.2 Teorema Fundamental do Cálculo
Corolário do Teorema Fundamental do Cálculo
Se a e b são números reais tais que a < b e
f : [a, b] → R
No que se segue vamos fazer as seguintes convenções
Z
a
é uma função contínua, então f é primitivável. Além disso, se
f (x) dx = 0
a
e
Z
b
a
f (x) dx = −
Z
b
F : [a, b] → R
f (x) dx.
é uma primitiva de f , então
a
Z
b
a
f (x) dx = F (b) − F (a).
Esta última igualdade designa-se por fórmula de Barrow.
António Bento (UBI)
Cálculo I
2010/2011
378 / 590
António Bento (UBI)
Cálculo I
2010/2011
380 / 590
§5.2 Teorema Fundamental do Cálculo
§5.2 Teorema Fundamental do Cálculo
A fórmula de Barrow costuma usar-se a seguinte notação
h
F (x)
ib
= F (b) − F (a).
a
Vejamos que a fórmula de Barrow é válida em condições mais gerais:
Exemplos (continuação)
Z π/2
b) Calculemos agora
sen x dx. Então
Z0 π/2
π/2
sen x dx = − cos x 0
0
π
− (− cos 0)
2
= 0 − (−1)
= 1.
= − cos
Fórmula de Barrow
Sejam a e b números reais tais que a < b e
f : [a, b] → R
c) Obviamente também se tem
Z π/2
π/2
cos x dx = sen x 0
uma função integrável à Riemann em [a, b] e primitivável em [a, b].
Então, representando por F uma primitiva de f , tem-se
Z
b
h
f (x) dx = F (x)
a
António Bento (UBI)
ib
a
0
π
− sen 0
2
= 1−0
= sen
= F (b) − F (a).
= 1.
Cálculo I
2010/2011
381 / 590
António Bento (UBI)
§5.2 Teorema Fundamental do Cálculo
Cálculo I
383 / 590
2010/2011
384 / 590
§5.2 Teorema Fundamental do Cálculo
Exemplos
Exemplos (continuação)
a) Calculemos
Z
1
d)
2
Z
x dx.
1
0
Pelo que vimos anteriormente, para calcularmos o integral dado,
basta termos uma primitiva da função
2
1
dx =
x3
Z
2
=
"
x−2
−2
=
1
− 2
2x
2
f (x) = x .
Como uma primitiva de f é a função dada por
F (x) =
temos
Z
0
António Bento (UBI)
2010/2011
1
2
x dx =
"
x3
3
#1
0
Cálculo I
x−3 dx
#2
1
2
1
1
1
=−
− −
2
2.2
2 . 12
1 1
=− +
8 2
3
=
8
x3
,
3
=
1
13 03
1
−
= .
3
3
3
2010/2011
382 / 590
António Bento (UBI)
Cálculo I
§5.2 Teorema Fundamental do Cálculo
Índice
Exemplos (continuação)
e)
Z
0
√
3
1
1
√
dx =
2
2
4−x
1
=
2
=
Z
Z
√
3
0
Z
√
0
√
3
0
3
1
p
dx
1 − x2 /4
1
dx
1 − (x/2)2
p
1/2
p
dx
1 − (x/2)2
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
Integral de Riemann: definição, propriedades e exemplos
Teorema Fundamental do Cálculo
Integração por partes e integração por substituição
Aplicações do cálculo integral
Integrais impróprios
6
Sucessões e séries
√
x 3
= arc sen
2 0
√
3
0
= arc sen
− arc sen
2
2
π
π
= −0=
3
3
António Bento (UBI)
1
Cálculo I
2010/2011
385 / 590
§5.2 Teorema Fundamental do Cálculo
António Bento (UBI)
Cálculo I
2010/2011
387 / 590
§5.3 Integração por partes e integração por substituição
Exemplos (continuação)
f)
Z
0
√
3
2
x2
1
dx =
6
4+x
4
=
Z
√
3
2
0
12
43
Z
x2
1
dx =
6
1 + x /4
4
√
3
3x2 /2
2
√
3
0
dx =
x2
dx
1 + (x3 /2)2
"
x3
3
#√
2
0
π
−0
4
=
Cálculo I
Integração por partes
Sejam a e b números reais tais a < b e
f, g : [a, b] → R
funções diferenciáveis com derivadas integráveis. Então
Z
b
a
1
[arc tg 1 − arc tg 0]
6
1
=
6
António Bento (UBI)
0
2
1
arc tg
6
2
1+
"
#
√
1
( 3 2)3
03
=
arc tg
− arc tg
6
2
2
=
(x3 /2)2
Z
h
f ′ (x)g(x) dx = f (x)g(x)
ib
a
−
Z
b
a
f (x)g′ (x) dx.
π
24
2010/2011
386 / 590
António Bento (UBI)
Cálculo I
2010/2011
388 / 590
§5.3 Integração por partes e integração por substituição
§5.3 Integração por partes e integração por substituição
Exemplos de integração por partes
a) Calculemos
Z
e
Exemplos de integração por partes (continuação)
ln x dx. Então
c)
1
Z
e
Z
ln x dx =
1
e
2
Z
2 x
x e dx =
0
1 . ln x dx
h
= x ln x
ie
1
−
e
= e −0 −
h
= e− x
e
x . (ln x)′ dx
1
Z
e
1
1
x . dx
x
2
= 4 e −2
1 dx
1
ie
h
= 2 ex
2010/2011
389 / 590
b)
x cos x dx =
0
(cos x) x dx
h
António Bento (UBI)
d) Calculemos
iπ
0
−
Z
0
π
(sen x) x′ dx
= (sen π) π − (sen 0) 0 −
0
h
π
Z
Z
π
Z
π/2
x
ex x
2
i2
0
Z
2
ex x dx
0
−
Z
2
i2
0
x
′
e x dx
0
0
= 2 e2 − e0
Z
2
x
e dx
0
= 2 e2 −2
Cálculo I
π/2
2010/2011
391 / 590
cos x ex dx:
cos x e dx =
0
sen x dx
0
sen x
π/2
ex 0
−
Z
π/2
sen x (ex ) dx
′
0
Z π/2
π π/2
e
− sen 0 e0 −
sen x ex dx
2
0
"
#
Z π/2
π/2
π/2
x ′
x
= e
− − cos x e 0 −
− cos x (e ) dx
0
iπ
Z π/2
h
i
π
= eπ/2 − − cos eπ/2 − − cos 0 e0 −
cos x ex dx
2
0
Z π/2
= eπ/2 −1 −
cos x ex dx.
0
= cos π − cos 0
= −1 − 1 = −2.
Cálculo I
= sen
− sen x dx
= cos x
António Bento (UBI)
ex (x2 )′ dx
0
= (sen x) x
=
0
Exemplos de integração por partes (continuação)
0
Z
2
§5.3 Integração por partes e integração por substituição
Exemplos de integração por partes (continuação)
π
Z
= 4 e −2 e 2 − e 0 −
1
Cálculo I
Z
h
2
§5.3 Integração por partes e integração por substituição
π
0
−
= e2 22 − e0 02 − 2
= 1.
Z
i2
h
= e − (e −1)
António Bento (UBI)
ex x2 dx
= ex x2
= e . ln e −1 . ln 1 −
Z
2
0
1
Z
Z
0
2010/2011
390 / 590
António Bento (UBI)
Cálculo I
2010/2011
392 / 590
§5.3 Integração por partes e integração por substituição
§5.3 Integração por partes e integração por substituição
Exemplos de integração por substituição
Z 4
√
1
√ dx fazendo a substituição t = x. Então
a) Calculemos
1
+
x
0
Exemplos de integração por partes (continuação)
d) (continuação) Acabámos de ver que
Z
π/2
0
cos x ex dx = eπ/2 −1 −
Z
π/2
x = t2 , pelo que dx = (t2 )′ dt = 2t dt.
cos x ex dx,
Além disso, quando x = 0 temos t = 0 e quando x = 4 vem t = 2. Assim,
Z 4
Z 2
Z 2
1
t
1
√ dx =
2t dt = 2
dt
1
+
t
1
+
t
1
+
x
0
0
0
Z 2
Z 2
1+t−1
1+t
1
=2
dt = 2
−
dt
1+t
1+t
0
0 1+t
Z 2
Z 2
2 2 1
dt = 2 t 0 − ln |1 + t| 0
=2
1 dt −
0
0 1+t
0
e, portanto,
2
o que implica
Z
Z
π/2
0
π/2
cos x ex dx = eπ/2 −1,
cos x ex dx =
0
eπ/2 −1
.
2
= 2 (2 − 0 − (ln 3 − ln 1)) = 4 − 2 ln 3.
António Bento (UBI)
Cálculo I
2010/2011
393 / 590
António Bento (UBI)
§5.3 Integração por partes e integração por substituição
b) Calculemos
Z
1
f : [a, b] → R
uma função contínua e
uma função diferenciável com derivada integrável e tal que
g(c)
António Bento (UBI)
f (x) dx =
c
d
x = t2 − 3
′
dx = t2 − 3
Além disso,
dt = 2t dt.
quando x = 1 vem t = 2
f (g(t))g′ (t) dt.
Cálculo I
x
√
dx. Para isso fazemos a substituição
x+3
√
t = x + 3,
e, portanto,
g([c, d]) ⊆ [a, b].
Z
6
isto é,
g : [c, d] → R
g(d)
395 / 590
Exemplos de integração por substituição (continuação)
Sejam a, b, c e d números reais tais que a < b e c < d,
Z
2010/2011
§5.3 Integração por partes e integração por substituição
Integração por substituição
Então
Cálculo I
e
quando x = 6 temos t = 3.
2010/2011
394 / 590
António Bento (UBI)
Cálculo I
2010/2011
396 / 590
§5.3 Integração por partes e integração por substituição
§5.3 Integração por partes e integração por substituição
Exemplos de integração por substituição (continuação)
Exemplos de integração por substituição (continuação)
b) (continuação) Assim,
c) (continuação) Para calcularmos
Z
6
1
x
√
dx =
x+3
Z
2
=2
=
=
=
=
António Bento (UBI)
3 t2
Z
3
2
1
1
A
B
= +
.
t(t + 1)
t
t+1
#3
t3
2
− 3t
3
2
27
8
2
−9−
−6
3
3
8
2 6−
3
20
3
Cálculo I
Então
A(t + 1) + Bt = 1,
pelo que quando t = 0 temos A = 1 e quando t = −1 vem B = −1
e, por conseguinte,
1
1
1
= −
.
t(t + 1)
t
t+1
2010/2011
397 / 590
§5.3 Integração por partes e integração por substituição
c) Para calcularmos
0
1
António Bento (UBI)
Z
1
0
x = ln t
1
0
António Bento (UBI)
1
dx =
x
e +1
Z
e
1
1 1
dt =
t+1 t
Cálculo I
Z
1
e
1
dx =
x
e +1
Z
e
1
dt
t(t + 1)
=
Z
e
1
1
−
dt
t
t+1
1
1
1
dt.
t
h
= ln |t| − ln |t + 1|
Além disso,
quando x = 0 temos t = 1 e quando x = 1 vem t = e.
Assim,
Z
399 / 590
c) (continuação) Assim,
o que implica
dx = (ln t)′ dt =
2010/2011
Exemplos de integração por substituição (continuação)
1
dx fazemos a substituição
x
e +1
ex = t,
e, portanto,
Cálculo I
§5.3 Integração por partes e integração por substituição
Exemplos de integração por substituição (continuação)
Z
1
dt
t(t + 1)
temos de determinar os números A e B tais que
t2 − 3 dt
"
e
Z
−3
2t dt
t
1
= ln e − ln(e +1) − (ln 1 − ln 2)
= 1 − ln
1
dt.
t(t + 1)
2010/2011
ie
398 / 590
António Bento (UBI)
e +1
.
2
Cálculo I
2010/2011
400 / 590
§5.3 Integração por partes e integração por substituição
Índice
Exemplos de integração por substituição (continuação)
Z 1
1
d) Calculemos
dx. Para isso usamos a substituição
2 2
−1 (1 + x )
1
dt.
cos2 t
′
x = tg t, o que implica dx = (tg t) dt =
Obviamente, atendendo a que t = arc tg x,
quando x = −1 tem-se t = arc tg(−1) = −
e
quando x = 1 vem t = arc tg(1) =
π
4
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
Integral de Riemann: definição, propriedades e exemplos
Teorema Fundamental do Cálculo
Integração por partes e integração por substituição
Aplicações do cálculo integral
Integrais impróprios
6
Sucessões e séries
π
.
4
Repare-se que
2 2
2
2
(1 + x ) = (1 + tg t) =
António Bento (UBI)
1
cos2 t
2
1
=
.
cos4 t
Cálculo I
2010/2011
401 / 590
António Bento (UBI)
§5.3 Integração por partes e integração por substituição
Cálculo I
2010/2011
403 / 590
§5.4 Aplicações do cálculo integral
Exemplos de integração por substituição (continuação)
d) (continuação) Assim,
Z
1
−1
1
dx =
(1 + x2 )2
Z
π/4
Z
π/4
=
1
2
1
=
2
−π/4
−π/4
=
1
1
dt =
4
1/ cos t cos2 t
1
cos(2t) + 1
dt =
2
2
sen(2t)
+t
2
Z
Z
π/4
cos2 t dt
Nesta secção veremos como aplicar o cálculo integral para
−π/4
• calcular a área de regiões planas;
π/4
cos(2t) + 1 dt
• calcular o comprimento de curvas planas;
−π/4
• calcular a área de superfície e o volume de um sólido de revolução.
π/4
−π/4
sen(π/2) π
sen(−π/2) π
+ −
−
2
4
2
4
1 1 π
1 π
π+2
=
+ − − −
=
2 2
4
2
4
4
António Bento (UBI)
Cálculo I
2010/2011
402 / 590
António Bento (UBI)
Cálculo I
2010/2011
404 / 590
§5.4 Aplicações do cálculo integral
§5.4 Aplicações do cálculo integral
Seja f : [a, b] → R uma função integrável tal que existe c ∈]a, b[ tal que
f (x) > 0 para qualquer x ∈ [a, c] e f (x) 6 0 para qualquer x ∈ [c, b].
y
Seja f : [a, b] → R uma função integrável tal que f (x) > 0 para
qualquer x ∈ [a, b].
y
f (x)
b
b
c
b
b
a
x
b
A=
Z
b
f (x) dx
a
a
b
x
A=
Z
c
a
António Bento (UBI)
Cálculo I
2010/2011
405 / 590
António Bento (UBI)
§5.4 Aplicações do cálculo integral
b
A=−
Z
b
b
f (x) dx
c
Cálculo I
2010/2011
407 / 590
Sejam f, g : [a, b] → R uma funções integráveis tal que f (x) > g(x) para
qualquer x ∈ [a, b].
f (x)
y
x
b
f (x) dx
a
A=
b
Z
b
a
f (x) − g(x) dx
g(x)
b
f (x)
b
b
b
a
António Bento (UBI)
Z
§5.4 Aplicações do cálculo integral
Seja f : [a, b] → R uma função integrável tal que f (x) 6 0 para
qualquer x ∈ [a, b].
y
a
f (x) dx −
Cálculo I
2010/2011
406 / 590
António Bento (UBI)
b
Cálculo I
x
2010/2011
408 / 590
§5.4 Aplicações do cálculo integral
§5.4 Aplicações do cálculo integral
Sejam f, g : [a, b] → R funções integráveis tal que existe c ∈]a, b[ tal que
f (x) > g(x) para qualquer x ∈ [a, c] e f (x) 6 g(x) para qualquer
x ∈ [c, b].
y
Exemplos do cálculo da área de figuras planas
a) (continuação) Façamos a representação geométrica da região e
calculemos a sua área.
Assim, a área do triângulo é
f (x)
y
g(x)
2
b
b
y=x
A=
b
Z
0
=
b
Z
0
1
b
a
c
b
b
x
A=
c
a
f (x) − g(x) dx +
António Bento (UBI)
Z
b
b
c
2010/2011
409 / 590
0
= 2 . 1 − 12 − (2 . 0 − 02 )
= 1.
Cálculo I
2010/2011
411 / 590
Exemplos do cálculo da área de figuras planas (continuação)
a) Calculemos a área da região plana limitada pelas rectas de equação
e
b) Calculemos a área da região plana limitada pela recta de equação
x = 0.
Como nenhuma destas rectas é paralela às outras duas, a região plana de
que queremos calcular a área é um triângulo. Calculemos os vértices desse
triângulo. Para isso temos de resolver os seguintes sistemas:
(
(
(
(
y=x
2−x=x
2 = 2x
x=1
⇔
⇔
⇔
y =2−x
——
——
y=1
(
(
y=x
y=0
⇔
x=0
x=0
(
(
y =2−x
y=2
⇔
x=0
x=0
Assim, a região plana de que queremos calcular a área é o triângulo de
vértices (1, 1), (0, 0) e (0, 2).
Cálculo I
i1
§5.4 Aplicações do cálculo integral
Exemplos do cálculo da área de figuras planas
António Bento (UBI)
h
x
António Bento (UBI)
§5.4 Aplicações do cálculo integral
y = 2−x
2 − 2x dx
g(x) − f (x) dx
Cálculo I
y = x,
1
2 − x − x dx
= 2x − x2
y = 2−x
1
Z
1
2010/2011
410 / 590
y =x+2
e pela parábola de equação
y = x2 .
Comecemos por calcular os pontos de intersecção das duas curvas:
(
(
(
y =x+2
x2 = x + 2
x2 − x − 2 = 0
⇔
⇔
y = x2
——
——
Como
2
x −x−2=0⇔x=
1±
√
1+8
1±3
⇔x=
⇔ x = 2 ∨ x = −1,
2
2
os pontos de intersecção são (2, 4) e (−1, 1).
António Bento (UBI)
Cálculo I
2010/2011
412 / 590
§5.4 Aplicações do cálculo integral
§5.4 Aplicações do cálculo integral
Exemplos do cálculo da área de figuras planas
Exemplos do cálculo da área de figuras planas (continuação)
b) (continuação) Representemos geometricamente a região do plano de que
queremos calcular a área.
Assim, a área é
y = x2
A=
y
−1
4
b
=
=
y =x+2
b
2
Z
1
=
2 x
-1
=
António Bento (UBI)
c) (continuação) Representemos geometricamente o triângulo e calculemos a
sua área.
Z 1
Z 2
A =
2
x + 2 − x dx
0
y
2
x2
x3
+ 2x −
2
3 −1
22
23
+ 2.2−
2
3
(−1)3
(−1)2
+ 2(−1) −
−
2
3
8 1
1
2+4− − +2−
3 2
3
9
.
2
Cálculo I
2010/2011
413 / 590
y = −x + 3
2
y = 2x
b
2
António Bento (UBI)
e
y = −x + 3.
A região do plano de que queremos calcular a área é um triângulo pois é
limitada por três rectas. Calculemos os seus vértices.
y = 2x
y = x/2
⇔
y = 2x
y = −x + 3
x/2 = 2x
——
⇔
⇔
x = 4x
——
−x + 3 = 2x
——
⇔
⇔
−3x = 0
——
−3x = −3
——
Z
2
x dx + 3
1
h
i
h
Cálculo I
Z
2
1 dx
1
i
2010/2011
415 / 590
⇔
⇔
x=0
y=0
x2 + y 2 = r 2 ⇔ y 2 = r 2 − x2
y
r
⇔ y=±
p
r 2 − x2
e, portanto, a curva que limita superiormente a zona sombreada é
x=1
y=2
y=
rx
p
r 2 − x2 .
Assim, a área do círculo de raio r é dada
por
Z rp
A=4
r 2 − x2 dx.
0
Assim, os vértices do triângulo são (0, 0), (1, 2) e (2, 1).
Cálculo I
1
3
x dx −
2
3x
+ 3 dx
2
d) Calculemos a área de um círculo de raio r. Por uma questão de simplicidade
vamos considerar o centro do círculo a origem. Obviamente, basta calcular a
área da parte do círculo que está no primeira quadrante e multiplicar esse valor
por quatro. Para isso temos encontrar a equação da curva que limita
superiormente a zona sombreada da figura. Da equação da circunferência temos
y = x/2
−x + 3 = x/2
−2x + 6 = x
−3x = −6
x=2
⇔
⇔
⇔
⇔
y = −x + 3
——
——
——
y=1
António Bento (UBI)
0
1
−
x
dx
2
2
3 x2 1 3 x2 2
−
+3 x 1
2 2 0 2 2 1
3 4
1
3 1
−0 −
−
+ 3 (2 − 1)
=
2 2
2 2
2
3
9
= − +3
4
4
3
= .
2
=
x
Z
1
2
Z
3x
dx +
2
−x + 3 −
Exemplos do cálculo da área de figuras planas (continuação)
c) Calculemos a área da região plana limitada pelas rectas de equação
x
2
3
=
2
b
1
1
0
b
1
Z
x
dx +
2
§5.4 Aplicações do cálculo integral
Exemplos do cálculo da área de figuras planas (continuação)
y=
=
x
y=
2
§5.4 Aplicações do cálculo integral
y = 2x,
2x −
2010/2011
414 / 590
António Bento (UBI)
Cálculo I
2010/2011
416 / 590
§5.4 Aplicações do cálculo integral
§5.4 Aplicações do cálculo integral
Exemplos do cálculo da área de figuras planas (continuação)
Z rp
d) (continuação) Para calcularmos A = 4
r2 − x2 dx temos de fazer a
Seja f : [a, b] → R uma função com derivada contínua.
y
y = f (x)
0
substituição
b
x = r sen t
b
e, portanto,
′
dx = (r sen t) dt = r cos t dt.
Além disso, como
x
r
t = arc sen
a
resulta que
e
ℓ=
π
quando x = r temos t = arc sen 1 = .
2
Cálculo I
2010/2011
417 / 590
António Bento (UBI)
A = 4
r 2 − x2 dx = 4
0
= 4r
Z
= 4r 2
π/2
q
π/2
p
r 2 (1 − sen2 t) cos t dt = 4r
0
Z
π/2
Z
π/2
= 2r 2
cos2 t dt = 4r 2
Z
π/2
0
= πr 2 .
António Bento (UBI)
sen 0
+0
2
sen(2t)
+t
2
Cálculo I
2010/2011
419 / 590
r cos t cos t dt
y
r
cos(2t) + 1
dt
2
h
cos(2t) + 1 dt = 2r 2
π
sen π
+ −
2
2
π/2
0
0
Z
Cálculo I
a) Calculemos o perímetro de uma circunferência de raio r. Para isso
consideremos como centro da circunferência a origem. Obviamente
basta considerar a parte da circunferência situada no primeiro
quadrante.
2
r 2 − (r sen t) r cos t dt
0
0
= 2r 2
Z
1 + [f ′ (x)]2 dx .
Exemplos do cálculo do comprimento de curvas planas
d) (continuação) Assim,
p
bq
§5.4 Aplicações do cálculo integral
Exemplos do cálculo da área de figuras planas (continuação)
r
Z
a
§5.4 Aplicações do cálculo integral
Z
x
O comprimento do gráfico de f é dado por
quando x = 0 temos t = arc sen 0 = 0
António Bento (UBI)
b
= 2r 2
iπ/2
rx
0
π
2
2010/2011
418 / 590
António Bento (UBI)
Cálculo I
2010/2011
420 / 590
§5.4 Aplicações do cálculo integral
§5.4 Aplicações do cálculo integral
Exemplos do cálculo do comprimentos de curvas planas (continuação)
Exemplos do cálculo do comprimento de curvas planas (continuação)
b) Calculemos o comprimento da curva y = x3/2 entre x = 0 e x = 1. Como
a) (continuação)
Da equação da circunferência x2 + y 2 = r2 , resulta
√
y = ± r2 − x2 . Como
p
′
x
r2 − x2 = − √
,
r2 − x2
temos
temos
r
s
r2
António Bento (UBI)
Cálculo I
2010/2011
1
4
=
9
Z
421 / 590
ε→0
ε→0
António Bento (UBI)
Cálculo I
2010/2011
423 / 590
Seja f : [a, b] → R uma função contínua.
y
r−ε
0
Z
s
r−ε
0
r−ε
2
x
dx
1 + −√
r2 − x2
y = f (x)
b
1
√
dx
2
r − x2
a
1/r
p
dx
1 − (x/r)2
0
h
x ir−ε
= lim+ 4r arc sen
ε→0
r 0
r−ε
= lim+ 4r arc sen
− arc sen 0
ε→0
r
π
= 4r (arc sen 1 − 0) = 4r = 2πr
2
= lim+ 4r
António Bento (UBI)
1
b
Z
= lim+ 4r
ε→0
p
1 + 9x/4 dx
§5.4 Aplicações do cálculo integral
Exemplos do cálculo do comprimento de curvas planas (continuação)
ℓ = lim+ 4
1
"
#1
9
4 (1 + 9x/4)3/2
1/2
(1 + 9x/4)
dx =
9
3/2
0 4
0
!
√
3/2
4 2 13
2 3/2
4 2 13 13 2
√ −
=
− 1
=
9 3
4
3
9 3 4 4
3
√
8
13 13
=
− .
27
27
§5.4 Aplicações do cálculo integral
a) (continuação) Assim,
Z
q
2
√
1 + 3 x/2 dx =
0
0
1
não está definida em x = r. Para
− x2
ultrapassarmos este problema vamos calcular o integral entre 0 e r − ε
onde ε é tal que 0 < ε < r e em seguida fazer ε tender para 0+ .
só que a função √
Z
ℓ=
s
2
Z r
x
x2
ℓ = 4
1 + −√
dx = 4
1+ 2
dx
r − x2
r2 − x2
0
0
s
Z r
Z r
r2 − x2 + x2
1
√
dx = 4r
dx,
= 4
2 − x2
2
r
r − x2
0
0
Z
′
3
3√
x3/2 = x1/2 =
x,
2
2
Z
Cálculo I
b
x
O volume do sólido de revolução que se obtém rodando em torno do
eixo dos xx a região situada entre o gráfico de f e o eixo dos xx é dado
por
V =π
Z
b
[f (x)]2 dx .
a
2010/2011
422 / 590
António Bento (UBI)
Cálculo I
2010/2011
424 / 590
§5.4 Aplicações do cálculo integral
§5.4 Aplicações do cálculo integral
Se f : [a, b] → R é uma função não negativa e com derivada contínua,
então a área de superfície do sólido de revolução que se obtém rodando
em torno do eixo dos xx a região situada entre o gráfico de f e o eixo
dos xx é dada por
AS = 2π
y
Z
b
a
q
f (x) 1 + [f ′ (x)]2 dx .
y = f (x)
b
b
a
António Bento (UBI)
x
b
Cálculo I
2010/2011
425 / 590
Volume e área de superfície de um sólido de revolução (continuação)
a) (continuação)
Já sabemos que temos de a equação da semicircunferência é
√
y = r2 − x2 , donde o volume da esfera de raio r é igual a
Z r p
2
V = π
r2 − x2 dx
−r
Z r
= π
r2 − x2 dx
−r
r
x3
2
= π r x−
3 −r
3
r
(−r)3
= π r3 −
− r2 (−r) −
3
3
3
r
= π 2r3 − 2
3
4 3
= πr .
3
António Bento (UBI)
§5.4 Aplicações do cálculo integral
Cálculo I
2010/2011
427 / 590
§5.4 Aplicações do cálculo integral
Volume e área de superfície de um sólido de revolução
a) Calculemos o volume e a área de superfície de uma esfera de raio r. Como
habitualmente vamos centrar a esfera na origem. Uma esfera de raio r
centrada na origem obtém-se rodando em torno do eixo dos xx um
semicírculo de centro na origem e de raio r.
y
António Bento (UBI)
Cálculo I
a) (continuação) Quanto à área da superfície esférica, atendendo a que
p
r 2 − x2
′
= −√
x
− x2
r2
temos novamente o mesmo problema que tivemos no cálculo do
perímetro de uma circunferência de raio r pois a derivada não está
definida em x = r e em x = −r. Este problema será resolvido da
mesma forma que o fizemos anteriormente, ou seja, vamos calcular
o integral entre −r + ε e r − ε e depois fazer ε tender para 0+ .
r x
−r
Volume e área de superfície de um sólido de revolução (continuação)
2010/2011
426 / 590
António Bento (UBI)
Cálculo I
2010/2011
428 / 590
§5.4 Aplicações do cálculo integral
§5.4 Aplicações do cálculo integral
Volume e área de superfície de um sólido de revolução (continuação)
a) (continuação) Assim,
AS =
=
=
=
Volume e área de superfície de um sólido de revolução (continuação)
b) (continuação) O volume é do cone é
s
2
x
lim 2π
1 + −√
dx
ε→0+
r2 − x2
−r+ε
s
Z r−ε p
x2
lim+ 2π
r2 − x2 1 + 2
dx
ε→0
r − x2
−r+ε
s
Z r−ε p
r2 − x2 + x2
dx
lim+ 2π
r2 − x2
r2 − x2
ε→0
−r+ε
Z r−ε
Z r−ε
lim+ 2π
r dx = lim+ 2πr
1 dx
Z
ε→0
r−ε
−r+ε
p
r2 − x2
ε→0
−r+ε
r−ε
= lim+ 2πr x −r+ε = lim+ 2πr (r − ε − (−r + ε))
ε→0
h
r 2
x dx
h
0
Z
πr2 h 2
= 2
x dx
h
0
h
πr2 x3
= 2
h
3 0
πr2 h3
03
= 2
−
h
3
3
V =π
ε→0
=
= lim+ 2πr (2r − 2ε) = 4πr2 .
Z
πr2 h
3
ε→0
António Bento (UBI)
Cálculo I
2010/2011
429 / 590
António Bento (UBI)
Cálculo I
§5.4 Aplicações do cálculo integral
2010/2011
431 / 590
§5.4 Aplicações do cálculo integral
Volume e área de superfície de um sólido de revolução (continuação)
b) Calculemos o volume e a área de superfície de um cone de altura h e raio
da base r. Para obtermos este cone basta pormos a rodar em torno do
eixo dos xx o segmento de recta que une os pontos (0, 0) e (h, r):
y
r
Volume e área de superfície de um sólido de revolução (continuação)
b) (continuação) A área de superfície do cone é
s
r
2
Z h
Z
r 2
r
r ′
2πr h
AS = 2π
x 1+
x
dx =
x 1+
dx
h
h 0
h
0 h
2πr
=
h
h
x
=
=
É óbvio que a equação do segmento é y =
António Bento (UBI)
Cálculo I
r
x com x ∈ [0, h]
h
2010/2011
430 / 590
Z
0
h
r
r2
2πr
x 1 + 2 dx =
h
h
2πr p 2
h + r2
h2
Z
h
2πr p 2
h + r2
h2
h2
0
−
2
2
António Bento (UBI)
x dx =
0
Z
h
r
x
0
h2 + r 2
dx
h2
2πr p 2
h + r2
h2
2
Cálculo I
= πr
p
x2
2
h
0
h2 + r 2
2010/2011
432 / 590
§5.5 Integrais impróprios
Índice
Suponha-se, no entanto, que
1
2
3
4
5
6
i) f está definida em [a, +∞[ e existe
Funções reais de variável real: generalidades e exemplos
Funções reais de variável real: limites e continuidade
Z
ii) f está definida em ] − ∞, b] e existe
ainda
Cálculo diferencial em R
u
f (x) dx para cada u ∈ [a, +∞[; ou
a
Z
b
t
iii) f está definida em ] − ∞, +∞[ e existe
Primitivas
u→+∞
a
ii)
Sucessões e séries
Z
b
f (x) dx = lim
t→−∞
−∞
iii)
Z
+∞
f (x) dx = lim
u
f (x) dx para cada t, u ∈ R.
t
2010/2011
433 / 590
a
b
Z
t→−∞
−∞
Cálculo I
Z
Nestas condições, temos, para cada uma das três situações consideradas, as
seguintes definições
Z +∞
Z u
i)
f (x) dx = lim
f (x) dx
Cálculo integral em R
Integral de Riemann: definição, propriedades e exemplos
Teorema Fundamental do Cálculo
Integração por partes e integração por substituição
Aplicações do cálculo integral
Integrais impróprios
António Bento (UBI)
f (x) dx para cada t ∈ ] − ∞, b]; ou
f (x) dx
t
Z
c
f (x) dx + lim
u→+∞
t
António Bento (UBI)
Z
u
f (x) dx
c
Cálculo I
§5.5 Integrais impróprios
2010/2011
435 / 590
§5.5 Integrais impróprios
Dizemos que os integrais
Z
Na definição do integral de Riemann de uma função
+∞
f (x) dx,
a
f : [a, b] → R
[a, b] fosse fechado e limitado
f (x) dx
−∞
e
Z
+∞
f (x) dx
−∞
Os integrais considerados designam-se por integrais impróprios de
primeira espécie.
e que a função
f fosse limitada.
Na definição iii) não há dependência do ponto c escolhido. Na prática
pode-se fazer
Z +∞
Z u
f (x) dx = lim
f (x) dx.
−∞
Cálculo I
b
existem ou que são convergentes quando existirem (finitos) os
limites indicados; se o limites não existirem dizemos que o respectivo
integral é divergente.
exigimos que o intervalo
António Bento (UBI)
Z
2010/2011
434 / 590
António Bento (UBI)
u→+∞ t
t→−∞
Cálculo I
2010/2011
436 / 590
§5.5 Integrais impróprios
§5.5 Integrais impróprios
Exemplos de integrais impróprios de primeira espécie
Z +∞
e−x dx:
a) Calculemos
0
Z
0
+∞
e−x dx = lim
Z
= lim
h
u
u→+∞ 0
u→+∞
= lim
u→+∞
e−x dx
− e−x
iu
0
− e−u −(− e0 )
= lim 1 − e−u
u→+∞
= 1 − e−∞
= 1−0
= 1.
António Bento (UBI)
Cálculo I
2010/2011
437 / 590
Exemplos de integrais impróprios de primeira espécie (continuação)
Z +∞
1
dx, ou seja, determinemos se
b) Estudemos a natureza do integral
α
x
1
o integral é convergente ou divergente. Comecemos por supor α 6= 1.
Então
Z +∞
Z u
1
dx
=
lim
x−α dx
α
u→+∞
x
1
1
−α+1 u
x
= lim
u→+∞ −α + 1
1
−α+1
u
1
= lim
−
u→+∞ −α + 1
−α + 1

 1
se α > 1
= α−1

+∞
se α < 1
António Bento (UBI)
Cálculo I
§5.5 Integrais impróprios
Exemplos de integrais impróprios de primeira espécie (continuação)
e−x dx é convergente. O valor
0
b) (continuação) Se α = 1, então
deste integral pode ser interpretado como sendo a área da região
sombreada da figura seguinte.
y = e−x
439 / 590
§5.5 Integrais impróprios
Exemplos de integrais impróprios de primeira espécie (continuação)
Z +∞
a) (continuação) Assim, o integral
2010/2011
Z
+∞
1
y
1
dx =
x
=
=
lim
u→+∞
lim
u→+∞
Z
u
1
1
dx
x
ln |x|
u
1
lim (ln |u| − ln |1|)
u→+∞
= ln (+∞) − 0
1
= +∞
x
António Bento (UBI)
Cálculo I
2010/2011
+∞
1
dx é convergente apenas quando α > 1. Neste
α
x
1
exemplo também podemos interpretar o integral como uma área.
Assim, o integral
438 / 590
António Bento (UBI)
Z
Cálculo I
2010/2011
440 / 590
§5.5 Integrais impróprios
§5.5 Integrais impróprios
Critério de comparação
Exemplos de integrais impróprios de primeira espécie (continuação)
Z +∞
c) Calculemos
−∞
Z
+∞
−∞
Sejam f, g : [a, +∞[→ R duas funções tais que existe c ∈ [a, +∞[ tal que
1
dx:
1 + x2
1
dx = lim
u→+∞
1 + x2
t→−∞
= lim
u→+∞
Z
u
t
h
0 6 f (x) 6 g(x) para qualquer x > c.
Então
i) se
1
dx
1 + x2
arc tg x
então
t
ii) se
f (x) dx também é convergente;
Z
+∞
f (x) dx é divergente,
a
então
Z
= π.
António Bento (UBI)
+∞
Z
a
u→+∞
t→−∞
g(x) dx é convergente,
a
iu
= lim (arc tg u − arc tg t)
π
π
= − −
2
2
+∞
Z
+∞
g(x) dx também é divergente.
a
Cálculo I
2010/2011
441 / 590
António Bento (UBI)
Cálculo I
§5.5 Integrais impróprios
Exemplos
c) (continuação) A igualdade
a) Consideremos o integral impróprio
+∞
−∞
1
dx = π
1 + x2
Z
1
2010/2011
444 / 590
1
√
dx.
1 + x3
1
1
1
6 √ = 3/2
06 √
x
1 + x3
x3
para qualquer x > 1 e que
Z +∞
1
dx é convergente,
3/2
x
1
y
y=
+∞
Atendendo a que
significa que a área da região sombreada na figura seguinte é π.
1
443 / 590
§5.5 Integrais impróprios
Exemplos de integrais impróprios de primeira espécie (continuação)
Z
2010/2011
1
1 + x2
pelo critério de comparação, alínea i), o integral
x
Z
1
António Bento (UBI)
Cálculo I
2010/2011
442 / 590
António Bento (UBI)
+∞
1
√
dx também é convergente.
1 + x3
Cálculo I
§5.5 Integrais impróprios
§5.5 Integrais impróprios
Exemplos (continuação)
b) Consideremos agora o integral impróprio
Z
Como
06
+∞
1
1
√
dx.
1 + x2
Observação
Também existem critérios de comparação para os integrais impróprios
da forma
Z b
f (x) dx
1
1
1
1
= p
= √
6 √
2
2
1+x
1 + 2x + x
1 + x2
(1 + x)
−∞
e
para qualquer x > 1 e usando o facto de que
Z +∞
1
dx é divergente,
1
+
x
1
Z
+∞
f (x) dx.
−∞
pelo critério de comparação, alínea ii), o integral
Z
+∞
1
1
√
dx também é divergente.
1 + x2
António Bento (UBI)
Cálculo I
2010/2011
445 / 590
António Bento (UBI)
Cálculo I
§5.5 Integrais impróprios
Suponhamos agora que f está definida em [a, b[ e que é integrável em
qualquer intervalo [a, u] com u ∈ [a, b[. Nesta condições define-se
Z b
Z u
f (x) dx = lim
f (x) dx.
b) (continuação) Vejamos que de facto o integral impróprio
1
+∞
1
dx é divergente.
1+x
De forma análoga define-se
Z b
a
t→a
Z
b
f (x) dx
t
Quando f está definida em [a, c[ ∪ ]c, b] para algum c ∈]a, b[ e f é integrável
em [a, u] e [t, b] para quaisquer u ∈ [a, c[ e t ∈ ]c, b], define-se
Z b
Z u
Z b
f (x) dx = lim−
f (x) dx + lim+
f (x) dx.
lim [ln |1 + u| − ln |1 + 1|]
u→+∞
= +∞ − ln 2
= +∞.
Cálculo I
f (x) dx = lim+
a
quando f é está definida em ]a, b] e f é integrável em qualquer intervalo [t, b]
com t ∈ ]a, b].
u→+∞
António Bento (UBI)
u→b−
a
Para isso basta usarmos a definição:
Z +∞
Z u
1
1
dx = lim
dx
u→+∞ 1 1 + x
1+x
1
u
= lim ln |1 + x| 1
=
447 / 590
§5.5 Integrais impróprios
Exemplos (continuação)
Z
2010/2011
a
2010/2011
446 / 590
António Bento (UBI)
u→c
a
Cálculo I
t→c
t
2010/2011
448 / 590
§5.5 Integrais impróprios
§5.5 Integrais impróprios
Exemplos de integrais impróprios de segunda espécie (continuação)
a) (continuação) Quando α = 1 temos
Z
Nos três casos considerados anteriormente o integral
b
a
Z
b
f (x) dx
b
1
dx
x
−
a
t
b
= lim+ ln(x − a) t
1
dx = lim+
x−a
t→a
Z
t→a
a
= lim+ (ln(b − a) − ln(t − a))
designa-se por integral impróprio de segunda espécie. O integral
diz-se convergente se existem e são finitos os limites indicados e
diz-se divergente quando tal não se verifica.
t→a
= ln(b − a) − ln(0+ )
= ln(b − a) − (−∞)
= +∞
Assim,
Z
a
António Bento (UBI)
Cálculo I
2010/2011
449 / 590
a
1
dx = lim+
(x − a)α
t→a
Z
b
= lim+
(x − a)−α+1
−α + 1
= lim+
(b − a)
−α + 1
t→a
t→a
António Bento (UBI)
t
Cálculo I
convergente
divergente
se α < 1;
se α > 1.
Cálculo I
2010/2011
451 / 590
Exemplos de integrais impróprios de segunda espécie (continuação)
Z b
1
b) Determinemos a natureza de
dx. Comecemos por fazer
α
a (b − x)
α 6= 1. Então
(x − a)−α dx

1−α

 (b − a)
1−α
=

+∞
(
§5.5 Integrais impróprios
Exemplos de integrais impróprios de segunda espécie
Z b
1
a) Calculemos
dx. Comecemos por supor que α 6= 1. Então
α
a (x − a)
b
1
dx é
(x − a)α
António Bento (UBI)
§5.5 Integrais impróprios
Z
b
Z
b
b
a
1
dx = lim −
(b − x)α
u→b−
Z
u
= lim− −
(b − x)−α+1
−α + 1
= lim− −
(b − u)−α+1
(b − a)−α+1
−
−α + 1
−α + 1
t
u→b
(t − a)
−α + 1
−α+1
−α+1
−
u→b
se α < 1
se α > 1
2010/2011
450 / 590
António Bento (UBI)
a
−(b − x)−α dx

1−α

 (b − a)
1−α
=

+∞
Cálculo I
u
a
se α < 1;
se α > 1
2010/2011
452 / 590
§5.5 Integrais impróprios
§5.5 Integrais impróprios
Exercícios
Calcule
Z +∞
2
a)
xe−x dx
Exemplos de integrais impróprios de segunda espécie (continuação)
b) (continuação) Para α = 1 vem
Z
b
a
1
dx = lim− −
b−x
u→b
u
1
−
dx
b−x
a
u
= lim − ln(b − x) a
Z
c)
0
−∞
u→b−
= lim− − (ln(b − u) − ln(b − a))
u→b
e)
Z
g)
Z
i)
Z
k)
Z
2
0
= − ln(0+ ) − ln(b − a)
= − (−∞ − ln(b − a))
π
2
Portanto,
0
−∞
a
António Bento (UBI)
b
1
dx é
(b − x)α
(
convergente
divergente
Cálculo I
se α < 1;
se α > 1.
2010/2011
1
453 / 590
1
dx
1 + x2
1
p
dx
|x − 1|
0
= +∞
Z
sen x
dx
1 − cos x
x
dx
1 + x4
+∞
1
dx
(1 + x2 ) arc tg x
António Bento (UBI)
§5.5 Integrais impróprios
Também existem critérios de comparação para os integrais impróprios
de segunda espécie.
Cálculo I
1
d)
Z
+∞
f)
Z
1
h)
Z
j)
Z
l)
Z
0
arc tg x
dx
1 + x2
x ln2 x dx
0
−∞
0
1
x
dx
1 + x2
1
dx
x(1 − ln x)
6
x5 ex dx
−∞
e
+∞
1
√
dx
x ln x − 1
Cálculo I
2010/2011
455 / 590
2010/2011
456 / 590
Índice
Observação
António Bento (UBI)
Z
0
Z
+∞
b)
2010/2011
454 / 590
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Séries de números reais
Séries de potências
António Bento (UBI)
Cálculo I
§6.1.1 Definição e exemplos
Índice
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Definição e exemplos
Sucessões limitadas e sucessões monótonas
Sucessões convergentes
Subsucessões
Infinitamente grandes
Séries de números reais
Séries de potências
António Bento (UBI)
Uma sucessão é uma correspondência que a cada número natural n
faz corresponder um e um só número real.
Assim, uma sucessão é uma função real de variável natural, ou seja,
uma sucessão é uma função
u : N → R.
Cálculo I
Para designarmos o valor da função em n costuma usar-se a notação
un em vez de u(n).
2010/2011
457 / 590
António Bento (UBI)
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Definição e exemplos
Sucessões limitadas e sucessões monótonas
Sucessões convergentes
Subsucessões
Infinitamente grandes
Séries de números reais
Séries de potências
António Bento (UBI)
2010/2011
459 / 590
§6.1.1 Definição e exemplos
Índice
1
Cálculo I
Aos valores
u1 , u2 , . . . , un , . . .
chamamos termos da sucessão e
ao valor u1 chamamos termo de ordem 1 ou primeiro termo
da sucessão;
ao valor u2 chamamos termo de ordem 2 ou segundo termo
da sucessão;
Cálculo I
ao valor u3 chamamos termo de ordem 3 ou terceiro termo da
sucessão;
etc
À expressão un chamamos termo geral da sucessão.
2010/2011
458 / 590
António Bento (UBI)
Cálculo I
2010/2011
460 / 590
§6.1.1 Definição e exemplos
§6.1.1 Definição e exemplos
Exemplos de sucessões (continuação)
Escreveremos
b) Consideremos a sucessão de termo geral un = (−1)n .
(u1 , u2 , . . . , un , . . .),
O primeiro termo desta sucessão é u1 = (−1)1 = −1.
O segundo termo desta sucessão é u2 = (−1)2 = 1.
ou
(un )n∈N ,
O terceiro termo desta sucessão é u3 = (−1)3 = −1.
O quarto termo desta sucessão é u4 = (−1)4 = 1.
ou simplesmente
(un )
E assim sucessivamente.
Podemos concluir que os termos de ordem par são todos iguais a 1 e
que os termos de ordem ímpar são todos iguais a −1. Assim, a lista
que se segue dá-nos todos os termos da sucessão
u(N) = {un : n ∈ N}
−1, 1, −1, 1, −1, 1, −1, 1, −1, 1, . . .
para indicar a sucessão u.
O conjunto
e o conjunto dos termos desta sucessão é
designa-se por conjunto dos termos da sucessão (un )n∈N .
u(N) = {−1, 1} .
António Bento (UBI)
Cálculo I
2010/2011
461 / 590
António Bento (UBI)
§6.1.1 Definição e exemplos
Cálculo I
2010/2011
463 / 590
2010/2011
464 / 590
§6.1.1 Definição e exemplos
Exemplos de sucessões
a) Façamos
isto é,
un = 1 para todo o n ∈ N,
Exemplos de sucessões (continuação)
c) Seja u a sucessão definida por
(1, 1, . . . , 1, . . .)
é a sucessão constante e igual a 1. Mais geralmente, dado c ∈ R e
fazendo
vn = c para qualquer n ∈ N,
un = n.
Então
u(N) = N.
temos a sucessão constante e igual a c. Neste caso
v(N) = {c} .
António Bento (UBI)
Cálculo I
2010/2011
462 / 590
António Bento (UBI)
Cálculo I
§6.1.1 Definição e exemplos
Índice
Exemplos de sucessões (continuação)
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Definição e exemplos
Sucessões limitadas e sucessões monótonas
Sucessões convergentes
Subsucessões
Infinitamente grandes
Séries de números reais
Séries de potências
d) Seja
1
para todo o n ∈ N.
n
Podemos escrever esta sucessão das seguintes formas:
un =
ou
1 1 1
1
1, , , , . . . , , . . . ,
2 3 4
n
1
n
ou
,
n∈N
1
.
n
Neste exemplo temos u(N) =
António Bento (UBI)
1
:n∈N .
n
Cálculo I
2010/2011
465 / 590
§6.1.1 Definição e exemplos
António Bento (UBI)
Cálculo I
2010/2011
467 / 590
§6.1.2 Sucessões limitadas e sucessões monótonas
Uma sucessão (un )n∈N diz-se limitada se existirem números reais a e b
tais que
a 6 un 6 b para todo o n ∈ N;
Observação
O exemplo a) mostra que
(un )n∈N
ou ainda, se existirem números reais a e b tais que
e
un ∈ [a, b] para todo o n ∈ N.
u(N)
Como todo o intervalo [a, b] está contido num intervalo da forma
[−c, c], para algum c ∈ R, uma sucessão (un ) é limitada se existir um
número real c > 0 tal que
são coisas diferentes e que, por conseguinte, não devem ser
confundidas. Neste exemplo tem-se
(un ) = (1, 1, 1, . . . , 1, . . .),
un ∈ [−c, c] para todo o n ∈ N,
enquanto que
o que é equivalente a existe c > 0 tal que
u(N) = {1} .
|un | 6 c para todo o n ∈ N.
Algo de semelhante acontece no exemplo b).
As sucessões que não são limitadas dizem-se ilimitadas.
António Bento (UBI)
Cálculo I
2010/2011
466 / 590
António Bento (UBI)
Cálculo I
2010/2011
468 / 590
§6.1.2 Sucessões limitadas e sucessões monótonas
§6.1.2 Sucessões limitadas e sucessões monótonas
Exemplos (continuação)
Exemplos
c) A sucessão un = n2 não é limitada. De facto,
a) A sucessão de termo geral
n
un = 4 + (−1) =
(
3
5
u1 = 1; u2 = 4; u3 = 9; u4 = 16; . . .
se n é ímpar;
se n é par;
pelo que a sucessão não é limitada superiormente.
d) A sucessão de termo geral vn = −n também não é limitada pois
é limitada pois
v1 = −1; v2 = −2; v3 = −3; . . .
3 6 un 6 5 para qualquer número natural n.
ou seja, esta sucessão não é limitada inferiormente.
António Bento (UBI)
Cálculo I
2010/2011
469 / 590
§6.1.2 Sucessões limitadas e sucessões monótonas
António Bento (UBI)
Cálculo I
2010/2011
471 / 590
§6.1.2 Sucessões limitadas e sucessões monótonas
Uma sucessão (un )n∈N diz-se crescente se
Exemplos (continuação)
un+1 > un para todo o n ∈ N
b) Consideremos a sucessão de termo geral
e diz-se decrescente se
n+2
un =
.
n
Como
un+1 6 un para todo o n ∈ N.
Equivalentemente, (un )n∈N é crescente se
n+2
n 2
2
= + =1+
n
n n
n
un+1 − un > 0 para todo o n ∈ N
podemos concluir que
e é decrescente se
1 6 un 6 3 para cada número natural n.
un+1 − un 6 0 para todo o n ∈ N.
Assim, esta sucessão é limitada.
Uma sucessão diz-se monótona se for crescente ou se for decrescente.
António Bento (UBI)
Cálculo I
2010/2011
470 / 590
António Bento (UBI)
Cálculo I
2010/2011
472 / 590
§6.1.2 Sucessões limitadas e sucessões monótonas
Índice
Exemplos de sucessões monótonas
a) Consideremos a sucessão de termo geral un =
un+1 − un
2n − 1
. Como
n+1
2(n + 1) − 1
2n − 1
=
−
(n + 1) + 1
n+1
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
=
2n + 1
2n − 1
−
n+2
n+1
4
Primitivas
=
(2n + 1)(n + 1) − (2n − 1)(n + 2)
(n + 1)(n + 2)
5
Cálculo integral em R
2n2 + 2n + n + 1 − (2n2 + 4n − n − 2)
(n + 1)(n + 2)
6
=
=
2n2 + 3n + 1 − 2n2 − 3n + 2
(n + 1)(n + 2)
=
3
>0
(n + 1)(n + 2)
Sucessões e séries
Sucessões de números reais
Definição e exemplos
Sucessões limitadas e sucessões monótonas
Sucessões convergentes
Subsucessões
Infinitamente grandes
Séries de números reais
Séries de potências
para qualquer número natural n, a sucessão é crescente.
António Bento (UBI)
Cálculo I
2010/2011
473 / 590
António Bento (UBI)
§6.1.2 Sucessões limitadas e sucessões monótonas
2(n + 1) + 1
2n + 1
−
n+1
n
2n + 3
2n + 1
=
−
n+1
n
un+1 − un =
A condição
é equivalente às condições
(2n + 3)n − (2n + 1)(n + 1)
=
n(n + 1)
2n + 3n − (2n + 2n + n + 1)
n(n + 1)
=
2n2 + 3n − 2n2 − 3n − 1
n(n + 1)
=
−1
60
n(n + 1)
Cálculo I
e un ∈ ]a − ε, a + ε[.
Assim, uma sucessão (un ) converge ou tende para um número real a
se para qualquer ε > 0, existe N ∈ N tal que
a − ε < un < a + ε para cada número natural n > N ;
ou se para qualquer ε > 0, existe N ∈ N tal que
un ∈ ]a − ε, a + ε[ para cada número natural n > N .
para qualquer número natural n. Logo a sucessão é decrescente.
António Bento (UBI)
|un − a| < ε
−ε < un − a < ε, a − ε < un < a + ε
2
=
475 / 590
Dados uma sucessão (un )n∈N e um número real a, dizemos que (un )
converge ou tende para a se para qualquer ε > 0, existe N ∈ N tal
que
|un − a| < ε para todo o número natural n > N .
2n + 1
, temos
n
2
2010/2011
§6.1.3 Sucessões convergentes
Exemplos de sucessões monótonas (continuação)
b) Para a sucessão de termo geral un =
Cálculo I
2010/2011
474 / 590
António Bento (UBI)
Cálculo I
2010/2011
476 / 590
§6.1.3 Sucessões convergentes
§6.1.3 Sucessões convergentes
Geometricamente, uma sucessão un tende para a se dado ε > 0 todos
os termos da sucessão estão na “faixa” limitada pela rectas y = a − ε e
y = a + ε a partir de determinada ordem. A figura seguinte ilustra esse
facto.
As sucessões constantes são convergentes. Se un = c para qualquer
número natural n, temos |un − c|=0 para cada n ∈ N, pelo que, dado
ε > 0, tomando N = 1 vem
|un − c| < ε para qualquer n > N .
b
a+ε
b
Logo (un ) converge para c.
b
a
b
1
A sucessão de termo geral un = converge para zero. De facto, dado
n
ε > 0, basta escolher um número natural N tal que N ε > 1 e, por
conseguinte, 1/N < ε. Assim, para n > N , temos
b
a−ε
b
b
b
1
2
3
4
N
|un − 0| = 1/n < 1/N < ε,
N +1 N +2 N +3 N +4
b
o que prova que un → 0.
Interpretação geométrica do limite de uma sucessão
António Bento (UBI)
Cálculo I
2010/2011
477 / 590
António Bento (UBI)
§6.1.3 Sucessões convergentes
Cálculo I
2010/2011
479 / 590
2010/2011
480 / 590
§6.1.3 Sucessões convergentes
Qualquer uma das notações
lim un = a,
n→∞
limn→∞ un = a,
Unicidade do limite
lim un = a,
Sejam (un ) uma sucessão e a e b dois números reais. Se
n
un → a e un → b,
lim un = a,
un → a
então
a = b.
é usada para exprimir o facto de que a sucessão (un ) converge para a.
Uma sucessão (un )n∈N diz-se convergente se existe um número real a
tal que un → a.
As sucessões que não são convergentes dizem-se divergentes.
António Bento (UBI)
Cálculo I
2010/2011
478 / 590
António Bento (UBI)
Cálculo I
§6.1.3 Sucessões convergentes
§6.1.3 Sucessões convergentes
Dadas duas sucessões u = (un )n∈N e v = (vn )n∈N de números reais,
define-se a soma de u e v, e designa-se por u + v, a sucessão cujo
termo de ordem n é un + vn , isto é,
Continuando a usar as sucessões u e v dadas por
1, 4, 9, . . . , n , . . .
(u + v)n = un + vn .
António Bento (UBI)
n
1 1
1
1.1, 4. , 9. , . . . , n2 . , . . .
2 3
n
e o quociente
1 4
9
n2
,
,
,...,
,...
1 1/2 1/3
1/n
un
=
.
vn
Cálculo I
2010/2011
481 / 590
1, 4, 9, . . . , n , . . .
e
1
1
1
1 + 1, 4 + , 9 + , . . . , n2 + , . . .
2
3
n
1 1
1
1, , , . . . , , . . . ,
2 3
n
=
1
1
1
1 − 1, 4 − , 9 − , . . . , n2 − , . . .
2
3
n
António Bento (UBI)
Cálculo I
=
= (1, 2, 3, . . . , n, . . .)
António Bento (UBI)
!
= 1, 8, 27, . . . , n3 , . . . .
Cálculo I
2010/2011
483 / 590
O produto de um infinitésimo por uma sucessão limitada é um
infinitésimo.
9 28
n3 + 1
2, , , . . . ,
,...
2 3
n
!
Exemplo
Para todo o x ∈ R, temos lim
n→∞
e a diferença de u e v, u − v, é a sucessão
As sucessões que convergem para zero designam-se por infinitésimos.
respectivamente, então u + v é a sucessão dada por
1 1
1
1, , , . . . , , . . . ,
2 3
n
§6.1.3 Sucessões convergentes
Assim, se u e v são as sucessões dadas por
2
u
é a sucessão
v
§6.1.3 Sucessões convergentes
e
e, na hipótese de vn 6= 0 para todo o n ∈ N,
u
v
o produto uv é a sucessão
De modo análogo se define a diferença, o produto e o quociente de
u e v (este último apenas na hipótese de se ter vn 6= 0 para todo o
n ∈ N):
(uv)n = un vn
(u − v)n = un − vn ,
2
!
1
sen(nx)
= sen(nx)
n
n
7 26
n3 − 1
0, , , . . . ,
,... .
2 3
n
2010/2011
482 / 590
sen(nx)
= 0. De facto,
n
é o produto de um infinitésimo por uma sucessão limitada e, portanto,
converge para zero.
António Bento (UBI)
Cálculo I
2010/2011
484 / 590
§6.1.3 Sucessões convergentes
§6.1.3 Sucessões convergentes
Álgebra dos limites
Seja f é um função com domínio contendo o conjunto dos números
naturais. Se
lim f (x) = a,
Sejam (un ) e (vn ) sucessões tais que lim un = a e lim vn = b. Então
a) (un + vn )n∈N é convergente e
x→+∞
lim(un + vn ) = lim un + lim vn = a + b;
então
b) (un − vn )n∈N é convergente e
lim f (n) = a.
n→+∞
lim(un − vn ) = lim un − lim vn = a − b;
c) (un . vn )n∈N é convergente e
Exemplo
lim(un . vn ) = lim un . lim vn = a . b;
un
d) se b 6= 0 e vn =
6 0 para todo o n ∈ N,
é convergente e
vn n∈N
lim
António Bento (UBI)
un
vn
=
Como
2010/2011
485 / 590
1
1+
n
n
= e.
lim
António Bento (UBI)
§6.1.3 Sucessões convergentes
= e,
temos
n→+∞
Cálculo I
x
lim
x→+∞
lim un
a
= .
lim vn
b
1
1+
x
Cálculo I
2010/2011
487 / 590
§6.1.3 Sucessões convergentes
Suponhamos que
un → a
e que todos os termos un pertencem ao domínio de uma função f . Se f
é contínua em a, então
f (un ) → f (a).
Como consequência imediata temos a seguinte propriedade.
Teorema da sucessão enquadrada
Sejam (un ), (vn ) e (wn ) sucessões e suponha-se que existe uma ordem
p ∈ N tal que
un 6 vn 6 wn para todo o número natural n > p.
Se un → a e wn → a, então
vn → a.
Seja (un ) uma sucessão convergente para a ∈ R e p > 0. Então
a) se un → a, então (un )p → ap ;
b) se un > 0 para todo o n ∈ N e un → a, então
António Bento (UBI)
Cálculo I
√
p
un →
√
p
a.
2010/2011
486 / 590
António Bento (UBI)
Cálculo I
2010/2011
488 / 590
§6.1.3 Sucessões convergentes
§6.1.3 Sucessões convergentes
Exemplo de aplicação do teorema da sucessão enquadrada
Vejamos que
r
4+
Como
26
1
4+ 2 6
n
r
s
1
4+4 +
n
1
→ 2.
n2
2
1
n
=
s
1
2+
n
2
=2+
1
n
As sucessões monótonas e limitadas são convergentes.
e
1
→ 2,
n
pelo teorema da sucessão enquadrada temos de ter
2+
r
4+
António Bento (UBI)
1
→ 2.
n2
Cálculo I
2010/2011
489 / 590
António Bento (UBI)
§6.1.3 Sucessões convergentes
Observação
O recíproco não é verdadeiro. A sucessão de termo geral un =
limitada, mas não é convergente.
(−1)n
é
Todas as sucessões ilimitadas são divergentes.
Exemplo
Já vimos que a sucessão de termo geral un = n2 não é limitada. Logo
não é convergente.
Cálculo I
2010/2011
491 / 590
2010/2011
492 / 590
Índice
Toda a sucessão convergente é limitada.
António Bento (UBI)
Cálculo I
2010/2011
490 / 590
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Definição e exemplos
Sucessões limitadas e sucessões monótonas
Sucessões convergentes
Subsucessões
Infinitamente grandes
Séries de números reais
Séries de potências
António Bento (UBI)
Cálculo I
§6.1.4 Subsucessões
§6.1.4 Subsucessões
Se (un ) é uma sucessão e (nk ) é uma sucessão de números naturais
estritamente crescente, isto é,
Teorema de Bolzano-Weierstrass
n1 < n2 < . . . < nk < nk+1 < . . . ,
Todas as sucessões limitadas têm subsucessões convergentes.
a sucessão
(unk ) = (un1 , un2 , . . . , unk , . . .)
diz-se uma subsucessão de (un ).
António Bento (UBI)
Cálculo I
2010/2011
493 / 590
António Bento (UBI)
§6.1.4 Subsucessões
Exemplo
A sucessão de termo geral
un = (−1)n
é divergente pois tem duas subsucessões que convergem para valores
diferentes.
Cálculo I
2010/2011
495 / 590
2010/2011
496 / 590
Índice
As subsucessões de uma sucessão convergente são convergentes para o
mesmo limite da sucessão.
António Bento (UBI)
Cálculo I
2010/2011
494 / 590
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Definição e exemplos
Sucessões limitadas e sucessões monótonas
Sucessões convergentes
Subsucessões
Infinitamente grandes
Séries de números reais
Séries de potências
António Bento (UBI)
Cálculo I
§6.1.5 Infinitamente grandes
§6.1.5 Infinitamente grandes
Existem sucessões divergentes que, pelas propriedades de que gozam,
merecem ser estudadas. Essas sucessões designam-se por infinitamente
grandes.
Exemplos
A sucessão de termo geral
un = n
tende para mais infinito, a sucessão de termo geral
Diz-se que uma sucessão (un ) tende para mais infinito ou que é um
infinitamente grande positivo, e escreve-se
un → +∞,
ou
vn = −n
tende para menos infinito e a sucessão de termo geral
lim un = +∞,
wn = (−1)n n
se para cada L > 0, existe N ∈ N tal que
tende para infinito. A sucessão (wn ) é um exemplo de um infinitamente
grande que não é nem um infinitamente grande positivo, nem um
infinitamente grande negativo.
un > L para qualquer natural n > N .
António Bento (UBI)
Cálculo I
2010/2011
497 / 590
António Bento (UBI)
§6.1.5 Infinitamente grandes
Cálculo I
2010/2011
499 / 590
§6.1.5 Infinitamente grandes
Observações
Se −un → +∞ diz-se que (un ) tende para menos infinito ou que a
sucessão (un ) é um infinitamente grande negativo e escreve-se
un → −∞,
ou
a) Os infinitamente grandes positivos e os infinitamente grandes
negativos, são infinitamente grandes. A sucessão de termo geral
lim un = −∞.
wn = (−1)n n
mostra que o contrário nem sempre se verifica.
b) Resulta imediatamente da definição que se un → +∞, então (un ) é
limitada inferiormente.
Diz-se ainda que (un ) tende para infinito ou que (un ) é um
infinitamente grande se |un | → +∞ e escreve-se
un → ∞
ou
c) Da definição resulta imediatamente que se (un ) e (vn ) são duas
sucessões tais que
lim un = ∞.
un 6 vn a partir de certa ordem e un → +∞,
então
António Bento (UBI)
Cálculo I
2010/2011
498 / 590
António Bento (UBI)
vn → +∞.
Cálculo I
2010/2011
500 / 590
§6.1.5 Infinitamente grandes
§6.1.5 Infinitamente grandes
Observação
Sejam (un ) e (vn ) duas sucessões de números reais.
Se
a) Se un → +∞ e (vn ) tende para a ∈ R ou para +∞, então
un → +∞
b) Se un → −∞ e (vn ) tende para a ∈ R ou para −∞, então
(+∞) + (−∞);
(un + vn ) → −∞.
este símbolo designa-se por símbolo de indeterminação. Algo de
semelhante acontece com
∞ − ∞.
c) Se un → ∞ e (vn ) tende para a ∈ R, então
(un + vn ) → ∞.
Cálculo I
vn → −∞,
então nada se pode dizer sobre (un + vn ) pois em alguns casos
(un + vn ) é convergente, noutros é divergente. Por isso, não fazemos
nenhuma convenção para o símbolo
(un + vn ) → +∞.
António Bento (UBI)
e
2010/2011
501 / 590
António Bento (UBI)
§6.1.5 Infinitamente grandes
Cálculo I
2010/2011
503 / 590
§6.1.5 Infinitamente grandes
Sejam (un ) e (vn ) duas sucessões de números reais.
Vê-se assim que pode usar-se a regra do limite da soma desde que se
adoptem as convenções
a) Se un → +∞ e se (vn ) tende para a > 0 ou tende para +∞, então
un .vn → +∞.
b) Se un → +∞ e se (vn ) tende para a < 0 ou tende para −∞, então
(+∞) + a = +∞ = a + (+∞)
(−∞) + a = −∞ = a + (−∞)
un .vn → −∞.
∞+a =∞=a+∞
c) Se un → −∞ e se (vn ) tende para a > 0 ou tende para +∞, então
(+∞) + (+∞) = +∞
un .vn → −∞.
(−∞) + (−∞) = −∞
d) Se un → −∞ e se (vn ) tende para a < 0 ou tende para −∞, então
onde a é um número real qualquer.
un .vn → +∞.
e) Se un → ∞ e (vn ) tende para a ∈ R \ {0} ou tende para ∞, então
un .vn → ∞.
António Bento (UBI)
Cálculo I
2010/2011
502 / 590
António Bento (UBI)
Cálculo I
2010/2011
504 / 590
§6.1.5 Infinitamente grandes
§6.1.5 Infinitamente grandes
Adoptando as convenções que se seguem, vê-se que se pode usar a
regra do limite do produto:
(+∞) × a = +∞ = a × (+∞) onde a ∈
Seja (un ) uma sucessão de termos não nulos.
a) Se un → ∞, então
R+
(−∞) × a = −∞ = a × (−∞) onde a ∈ R+
1
→ 0.
un
b) Se un → 0, então
1
→ ∞.
un
c) Se un → 0 e un > 0 a partir de certa ordem, então
(+∞) × a = −∞ = a × (+∞) onde a ∈ R−
(−∞) × a = +∞ = a × (−∞) onde a ∈ R−
∞ × a = ∞ = a × ∞ onde a ∈ R \ {0}
1
→ +∞.
un
(+∞) × (+∞) = +∞ = (−∞) × (−∞)
(+∞) × (−∞) = −∞ = (−∞) × (+∞)
d) Se un → 0 e un < 0 a partir de certa ordem, então
∞×∞=∞
António Bento (UBI)
1
→ −∞.
un
Cálculo I
2010/2011
505 / 590
António Bento (UBI)
§6.1.5 Infinitamente grandes
Cálculo I
2010/2011
507 / 590
§6.1.5 Infinitamente grandes
A regra do limite quociente pode manter-se desde que se adoptem as
seguintes convenções
Observação
1
=0
∞
Não se faz nenhuma convenção para os símbolos
0 × (+∞),
1
= +∞
0+
1
= −∞
0−
onde 0+ significa que
0 × (−∞)
e
1
=∞
0
un → 0 e un > 0 a partir de certa ordem
0 × ∞,
e 0− significa que
pois são símbolos de indeterminação.
un → 0 e un < 0 a partir de certa ordem.
António Bento (UBI)
Cálculo I
2010/2011
506 / 590
António Bento (UBI)
Cálculo I
2010/2011
508 / 590
§6.1.5 Infinitamente grandes
§6.1.5 Infinitamente grandes
Exemplo (continuação)
a) (continuação) Assim,
Observação
Os símbolos
∞
∞
e
0
0
n
lim a =


+∞






1



se a > 1
se a = 1
0
se −1 < a < 1





não existe




são símbolos de indeterminação.
se a = −1
se a < −1
∞
António Bento (UBI)
Cálculo I
2010/2011
509 / 590
António Bento (UBI)
§6.1.5 Infinitamente grandes
Cálculo I
2010/2011
§6.1.5 Infinitamente grandes
Exemplo (continuação)
Exemplo
b) Calculemos lim (3n − 2n ). Como lim 3n = +∞ e lim 2n = +∞,
temos uma indeterminação do tipo
a) Dado a ∈ R, consideremos a sucessão de termo geral un = an .
Se a > 1, então temos an → +∞.
∞ − ∞.
Quando a = 1, então un = 1n = 1 pelo que a sucessão tende para 1.
No entanto, pondo em evidência 3n temos
n
n
n
lim (3 − 2 ) = lim 3
Se a < −1, então an → ∞.
n
n
2n
1− n
3
Para a = −1 obtemos a sucessão (−1) que já vimos anteriormente.
Esta sucessão é divergente.
= lim 3
Se −1 < a < 1, então an → 0.
= +∞ × 1
António Bento (UBI)
511 / 590
Cálculo I
1−
n 2
3
= +∞ × (1 − 0)
= +∞
2010/2011
510 / 590
António Bento (UBI)
Cálculo I
2010/2011
512 / 590
§6.1.5 Infinitamente grandes
Índice
Exemplo (continuação)
2n + 5n+1
c) Calculemos lim n+1
. Temos uma indeterminação pois
2
+ 5n
lim
2n + 5n+1
+∞ + (+∞)
+∞
=
=
.
2n+1 + 5n
+∞ + (+∞)
+∞
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Séries de números reais
Definição, exemplos e primeiras propriedades
Séries de termos não negativos
Séries de termos sem sinal fixo
Séries de potências
Podemos levantar a indeterminação da seguinte forma
lim
2n + 5n+1
2n+1 + 5n
António Bento (UBI)
2n 5n × 5
+
n
n
2 +5 ×5
5n
5n
= lim n
=
lim
n
n
2
×
2
5n
2 ×2+5
+
5n
5n
n
2
+5
0+5
5
= lim n
=
=5
2
0×2+1
×2+1
5
Cálculo I
2010/2011
513 / 590
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Séries de números reais
Definição, exemplos e primeiras propriedades
Séries de termos não negativos
Séries de termos sem sinal fixo
Séries de potências
Cálculo I
2010/2011
515 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
Índice
1
António Bento (UBI)
Paradoxo de Aquiles
António Bento (UBI)
Cálculo I
Numa corrida entre um atleta velocista (Aquiles) e uma tartaruga é
dada uma vantagem inicial em termos de distância à tartaruga. Zenão
defende que Aquiles jamais alcançará a tartaruga porque quando
chegar ao ponto onde a tartaruga partiu, ela já terá percorrido uma
nova distância; e quando Aquiles percorrer essa nova distância, a
tartaruga já terá percorrido uma nova distância e assim sucessivamente.
Este famoso paradoxo foi proposto por Zenão da Elea no século V a.c..
2010/2011
514 / 590
António Bento (UBI)
Cálculo I
2010/2011
516 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
200 m
40 m
§6.2.1 Definição, exemplos e primeiras propriedades
Se (an ) é uma sucessão de números reais, chamaremos série gerada por
(an ) à expressão
a1 + a2 + · · · + an + · · ·
8m
obtida por adição (formal) dos termos da sucessão.
Suponhamos que a vantagem inicial que Aquiles dá à tartaruga é
200 m, que a velocidade de Aquiles é 5 m/s e que a velocidade da
200
tartaruga é 1 m/s. Aquiles demora
= 40 s para chegar ao ponto de
5
onde a tartaruga partiu. Entretanto, a tartaruga percorreu
40
1 × 40 = 40 m. Em seguida, Aquiles demorou
= 8 s para chegar onde
5
a tartaruga estava e a tartaruga andou 1 × 8 = 8 m e assim
sucessivamente...
A cada série fica associada uma sucessão (sn ), a que se chama
sucessão das somas parciais de (an ), definida por
s1 = a1
s2 = a1 + a2
s3 = a1 + a2 + a3
..
.
sn = a1 + a2 + · · · + an
..
.
Será que Aquiles consegue alcançar a tartaruga?
António Bento (UBI)
Cálculo I
2010/2011
517 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
2010/2011
519 / 590
A série diz-se convergente ou divergente conforme seja convergente
ou divergente a sucessão das somas parciais (sn ). Quando a série é
convergente, o limite da sucessão (sn ) designa-se por soma ou valor
da série.
200
metros; no ponto seguinte Aquiles percorreu (no total)
200
200 +
5
metros; no terceiro ponto Aquiles percorreu
Para representarmos a série (ou a sua soma, quando exista) usam-se os
símbolos
200 200/5
200 200
+
= 200 +
+ 2
5
5
5
5
metros; no quarto ponto Aquiles percorreu
200 200 200
+ 2 + 3
200 +
5
5
5
metros; e assim sucessivamente. O paradoxo de Aquiles tem por detrás
aquela que, provavelmente, foi a primeira série da história!
200 +
Cálculo I
Cálculo I
§6.2.1 Definição, exemplos e primeiras propriedades
No primeiro ponto, o ponto inicial da tartaruga, Aquiles percorreu
António Bento (UBI)
António Bento (UBI)
2010/2011
518 / 590
a1 + a2 + · · · + an + · · · ;
∞
X
n=1
an ;
X
an
e o contexto onde se usam estes símbolos indicará se estão a
representar a série ou a sua soma.
Dizemos que duas séries são da mesma natureza se são ambas
convergentes ou ambas divergentes.
António Bento (UBI)
Cálculo I
2010/2011
520 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
§6.2.1 Definição, exemplos e primeiras propriedades
Exemplo (continuação)
Observação
Em certos casos pode haver vantagem em que o primeiro valor que o
índice n toma seja um inteiro diferente de um, o que não traz nenhuma
dificuldade na teoria que irá ser exposta. Assim,
∞
X
1
n−1
n=2
De facto, atendendo a que
sn =
∞
X
1
n+1
n=0
e
=
n
e portanto
2
= 2.
n+1
Conclui-se que a série converge e tem soma s = 2.
Cálculo I
2010/2011
521 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
∞
X
2
, representamos abaixo os primeiros termos da
n(n + 1)
n=1
2
sucessão de termo geral an =
e da sucessão (sn ) das somas parciais
n(n + 1)
2
s2
b
a1
b
b
b
b
s10
s9
s8
s7
s6
s5
b
s4
b
s3
b
b
Série harmónica
A série
b
a3
b
2
3
a4
b
4
a5
b
5
Cálculo I
2010/2011
523 / 590
∞
X
1
n
n=1
designa-se por série harmónica. Consideremos ainda a respectiva sucessão
das somas parciais e tomemos a subsucessão dessa com termos com índice da
forma 2k , ou seja, a subsucessão (s2k ):
s22
a2
a6
a7
a8
a9
a10
b
b
b
b
b
6
7
8
9
10
s23
1
1
>
2
2
1 1
1
1
1
= s2 + + > + 2 × = 2 ×
3 4
2
4
2
1 1 1 1
1
1
1
= s22 + + + + > 2 × + 4 × = 3 ×
5 6 7 8
2
8
2
k
k
Em geral temos s2k > . Como lim = +∞, concluímos que lim sn = +∞ e,
2
2
consequentemente, a série harmónica é divergente.
Aparentemente a sucessão das somas parciais aproxima-se de 2...
António Bento (UBI)
António Bento (UBI)
s2 = 1 +
s1
1
s = lim sn = lim 2 −
§6.2.1 Definição, exemplos e primeiras propriedades
Exemplo
b
2
2
−
k k+1
2 2 2 2 2
2
2
+ − + − + ···+ −
2 2 3 3 4
n n+1
2
= 2−
n+1
designa uma série diferente.
Para a série
2
k(k + 1)
= 2−
∞
X
1
António Bento (UBI)
k=1
n
X
k=1
designam a mesma série, enquanto que
n=6
n
X
2
2
2
= −
conclui-se que
k(k + 1)
k k+1
Cálculo I
2010/2011
522 / 590
António Bento (UBI)
Cálculo I
2010/2011
524 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
§6.2.1 Definição, exemplos e primeiras propriedades
Série geométrica
Dado r ∈ R, consideremos a série
∞
P
r n que habitualmente se designa
n=0
por série geométrica. A sucessão (sn )n∈N0 das somas parciais será,
neste exemplo, dada por
sn = 1 + r + · · · + r n =
Isto permite-nos concluir que
a série geométrica é
(

n+1

1 − r
1−r
se r = 1.
convergente
divergente
se |r| < 1,
se |r| > 1.
Além disso, quando |r| < 1 a sua soma é igual a
António Bento (UBI)
se r 6= 1

n + 1
Cálculo I
X
X
bn é uma série divergente, então
X
bn são duas séries divergentes, a
an é uma série convergente e
X
é uma série divergente.
Note-se no entanto que, se
série
X
(an + bn )
an e
X
(an + bn )
pode ser convergente ou divergente.
1
.
1−r
2010/2011
Se
525 / 590
António Bento (UBI)
§6.2.1 Definição, exemplos e primeiras propriedades
Cálculo I
2010/2011
527 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
Exemplos
X
X
Sejam
an e
bn duas séries convergentes cujas somas são A e B,
respectivamente. Então a série
X
a) A série
+∞ X
n=1
1
1
+ n−1
n(n + 1)
5
+∞
X
(an + bn )
n=1
é convergente porque as séries
1
n(n + 1)
e
n=1
também são convergentes. Além disso, como
é convergente e a sua soma é A + B.
+∞
X
n=1
+∞
X
1
5n−1
+∞
X1
1
2
=
,
n(n + 1)
2 n(n + 1)
n=1
podemos concluir que a sua soma é 1 pois já sabemos que soma da série
X
Seja
an uma série convergente cuja soma é A e seja λ um número
real. Então a série
X
(λan )
é convergente e a sua soma é λA.
+∞
X
+∞ X
n=1
António Bento (UBI)
Cálculo I
2010/2011
526 / 590
+∞
+∞
X 1
X 1
2
é 2. Quanto à série
=
é uma série geométrica
n−1
n(n + 1)
5
5n
n=1
n=1
n=0
1
1
5
de razão e a sua soma é
= . Assim, a soma da série
5
1 − 1/5
4
1
1
+ n−1
n(n + 1)
5
António Bento (UBI)
é 1+
5
9
= .
4
4
Cálculo I
2010/2011
528 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
§6.2.1 Definição, exemplos e primeiras propriedades
Exemplos (continuação)
b) A série
+∞
X
n=1
7
3n−1
+
1
n
Nem sempre é fácil calcular a soma de uma série convergente, não se
conhecendo mesmo uma expressão para a soma de algumas séries
bastante simples. Assim, no que se segue, vamos estudar critérios que
nos permitem saber se uma série é ou não convergente, sem estarmos
preocupados com a soma no caso da série ser convergente.
é divergente porque a série
+∞
X
n=1
7
3n−1
=
+∞
X
n=1
7
n−1
1
3
é convergente e a série
+∞
X
1
n
n=1
é divergente.
António Bento (UBI)
Cálculo I
2010/2011
529 / 590
António Bento (UBI)
§6.2.1 Definição, exemplos e primeiras propriedades
X
200 +∞
1
=
200
n
5
5
n=0
n=0
n Se
António Bento (UBI)
5
= 250 m.
4
Cálculo I
531 / 590
X
an é uma série convergente, então lim an = 0.
Assim, se (an ) não converge para 0, a série an é divergente. Por
exemplo, a série
X n
n+1
n
converge para um.
é divergente porque a sucessão
n + 1 n∈N
P
.
1
1
Como série geométrica de razão é convergente pois < 1 e a sua
5
5
1
5
soma é
= , o ponto onde Aquiles ultrapassa a tartaruga é
1 − 1/5
4
200 ×
2010/2011
§6.2.1 Definição, exemplos e primeiras propriedades
Voltemos ao exemplo inicial de Aquiles e da tartaruga. A série
envolvida neste exemplo é
+∞
X
Cálculo I
2010/2011
530 / 590
No entanto, o recíproco deste teorema não é válido pois a série
harmónica
X1
n
1
convergir para zero.
é divergente apesar da sucessão
n n∈N
António Bento (UBI)
Cálculo I
2010/2011
532 / 590
§6.2.1 Definição, exemplos e primeiras propriedades
Sejam
X
an e
X
§6.2.2 Séries de termos não negativos
bn duas séries. Suponhamos que existe N ∈ N tal que
Nesta secção
Xvamos estudar séries de números reais não negativos, ou
seja, séries
an tais que
an > 0 para cada n ∈ N.
an = bn para qualquer número natural n > N.
Obviamente, pelo que já vimos anteriormente, a teoria que vamos
apresentar mantém-se válida se
Então
são da mesma natureza.
António Bento (UBI)
X
an e
X
bn
Cálculo I
an > 0 a partir de certa ordem.
2010/2011
533 / 590
António Bento (UBI)
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Séries de números reais
Definição, exemplos e primeiras propriedades
Séries de termos não negativos
Séries de termos sem sinal fixo
Séries de potências
António Bento (UBI)
535 / 590
Critério geral de comparação
Sejam
a) Se
Cálculo I
2010/2011
§6.2.2 Séries de termos não negativos
Índice
1
Cálculo I
b) Se
2010/2011
534 / 590
X
an e
X
bn é convergente, então
X
X
bn séries de termos não negativos tais que
0 6 an 6 bn a partir de certa ordem.
an é divergente, então
António Bento (UBI)
X
X
an também é convergente.
bn também é divergente.
Cálculo I
2010/2011
536 / 590
§6.2.2 Séries de termos não negativos
§6.2.2 Séries de termos não negativos
Exemplos de aplicação do critério geral de comparação
a) Consideremos a série
∞
X
1
n=1
n2
Exemplos de aplicação do critério geral de comparação (continuação)
. Uma vez que
c) A série
∞
X
1
1
2
2
06 2 =
6
para qualquer número natural n
n
n(2n)
n(n + 1)
pois
e, como vimos anteriormente, a série
06
∞
X
2
n(n + 1)
n=1
n=1
António Bento (UBI)
n2
06
e a série
2010/2011
537 / 590
António Bento (UBI)
n2
As séries
nα
António Bento (UBI)
∞
X
1
, α > 2.
α
n=1
+∞
X
1
é
α
n
n=1
também é convergente quando α > 2.
Cálculo I
539 / 590
2010/2011
nα
,
com α ∈ R, designam-se por séries de Dirichlet. Nos exemplos
anteriores já estudámos a natureza destas séries quando α 6 1 e α > 2.
Quando 1 < α < 2, a série é convergente. Assim,
é convergente, a série
X 1
2010/2011
Séries de Dirichlet
∞
X
1
n
Cálculo I
§6.2.2 Séries de termos não negativos
1
1
6 2 para qualquer n ∈ N e qualquer α > 2
α
n
n
X 1
X1
é divergente.
Exemplos de aplicação do critério geral de comparação (continuação)
Como
1
1
6 α para cada n ∈ N e para cada α 6 1
n
n
n
§6.2.2 Séries de termos não negativos
n=1
é divergente para α 6 1
é convergente.
Cálculo I
b) Estudemos a série
nα
e a série
é convergente, podemos afirmar que a série
∞
X
1
n=1
538 / 590
António Bento (UBI)
(
convergente
divergente
Cálculo I
se α > 1,
se α 6 1.
2010/2011
540 / 590
§6.2.2 Séries de termos não negativos
§6.2.2 Séries de termos não negativos
Critério do limite
X
X
Sejam
an e
bn séries de termos não negativos com bn 6= 0 para
cada n ∈ N.
an
a) Se lim
= ℓ com ℓ 6= 0 e ℓ 6= +∞, então as séries
bn
b) Se lim
c) Se lim
X
X
an e
sen
∞
X
1
sen . É óbvio que
n
n=1
1
>0 e
n
lim
an também é convergente.
X
e
2010/2011
∞
X
1
n=1
an também é divergente.
Cálculo I
1
> 0 para cada n ∈ N.
n
Como
X
an
= +∞ e a série
bn é divergente, então a série
bn
António Bento (UBI)
b) Consideremos a série
bn são da mesma natureza.
X
an
= 0 e a série
bn é convergente, então a série
bn
X
Exemplos de aplicação do critério do limite (continuação)
541 / 590
n
é divergente,
∞
X
sen
n=1
António Bento (UBI)
§6.2.2 Séries de termos não negativos
sen
1
n
1
n =1
1
também é divergente.
n
Cálculo I
2010/2011
543 / 590
§6.2.2 Séries de termos não negativos
Exemplos de aplicação do critério do limite
a) A série
∞
X
3n2 + 4
é convergente porque
2n4 + 3n + 1
n=1
3n2
+4
>0 e
2n4 + 3n + 1
e
Critério de D’Alembert (para séries de termos positivos)
Seja
1
> 0 para qualquer n ∈ N,
n2
3n2 + 4
4
3n4 + 4n2
3
lim 2n + 3n + 1 = lim 4
=
1
2n + 3n + 1
2
n2
∞
X
1
n=1
António Bento (UBI)
n2
X
an uma série de termos positivos tal que
a) Se λ < 1, então
b) Se λ > 1, então
lim
X
X
an+1
= λ.
an
an é convergente.
an é divergente.
é convergente.
Cálculo I
2010/2011
542 / 590
António Bento (UBI)
Cálculo I
2010/2011
544 / 590
§6.2.2 Séries de termos não negativos
§6.2.2 Séries de termos não negativos
Exemplos de aplicação do critério de D’Alembert
a) Provemos que a série
X 2n n!
nn
é convergente. É óbvio que
Critério de Cauchy (para séries de termos não negativos)
2n n!
> 0 qualquer que seja n ∈ N.
nn
X
Seja
Como
2
(n + 1)!
2n+1 (n + 1)! nn
2(n + 1)nn
(n + 1)n+1
= lim
= lim n
= lim
n
n+1
2 n!
2 n! (n + 1)
(n + 1)n+1
n
n
2nn
2
2
2
= lim
= lim
= lim
< 1,
n =
(n + 1)n
(n + 1)n /nn
e
(1 + 1/n)
an uma série de termos não negativos tal que
lim
√
n
an = λ.
n+1
lim
an+1
an
pelo critério de D’Alembert, a série
António Bento (UBI)
X 2n n!
nn
X
a) Se λ < 1, então
X
b) Se λ > 1, então
an é convergente.
an é divergente.
é convergente.
Cálculo I
2010/2011
545 / 590
António Bento (UBI)
Cálculo I
§6.2.2 Séries de termos não negativos
2010/2011
§6.2.2 Séries de termos não negativos
Exemplos de aplicação do critério de D’Alembert (continuação)
Exemplos de aplicação do critério de Cauchy
b) A série
a) Vejamos que a série
é divergente. Como
X
n
é divergente. Como
e
an+1
(n + 1) 3n+1
n+1
= lim
= lim 3
= lim 3
an
n 3n
n
1
1+
= 3 > 1,
n
pelo critério de D’Alembert a série
é divergente.
António Bento (UBI)
X
X n + 1 n2
n3n
n3n > 0 para cada n ∈ N
lim
547 / 590
n2
> 0 qualquer que seja n ∈ N
e
√
lim n an = lim
n3n
Cálculo I
n+1
n
s
n
n+1
n
n2
= lim
pelo critério de Cauchy, a série
2010/2011
546 / 590
António Bento (UBI)
n+1
n
n
n
1
= lim 1 +
= e > 1,
n
X n + 1 n2
Cálculo I
n
é divergente.
2010/2011
548 / 590
§6.2.2 Séries de termos não negativos
§6.2.3 Séries de termos sem sinal fixo
Exemplos de aplicação do critério de Cauchy (continuação)
b) À série
X
n 3n
Critério de Leibniz
também podemos aplicar o critério de Cauchy. Como
Se (an ) é uma sucessão decrescente convergente para zero, então a série
n 3n > 0 para cada n ∈ N
e
lim
√
n
an = lim
√
n
n
3n
+∞
X
(−1)n an
n=1
√
n
= lim 3 n = 3 · 1 = 3,
é convergente.
o critério de Cauchy garante-nos que
é divergente.
António Bento (UBI)
X
n 3n
Cálculo I
2010/2011
549 / 590
António Bento (UBI)
Cálculo I
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
551 / 590
§6.2.3 Séries de termos sem sinal fixo
Índice
1
2010/2011
Observações
a) Se (an ) é uma sucessão decrescente convergente para zero, então
an > 0 para qualquer n ∈ N.
b) As séries da forma
+∞
X
(−1)n an
n=1
6
designam-se por séries alternadas.
Sucessões e séries
Sucessões de números reais
Séries de números reais
Definição, exemplos e primeiras propriedades
Séries de termos não negativos
Séries de termos sem sinal fixo
Séries de potências
António Bento (UBI)
Cálculo I
c) O critério de Leibniz também é válido para séries da forma
+∞
X
(−1)n+1 an
ou da forma
n=1
2010/2011
550 / 590
António Bento (UBI)
+∞
X
(−1)n an .
n=k
Cálculo I
2010/2011
552 / 590
§6.2.3 Séries de termos sem sinal fixo
§6.2.3 Séries de termos sem sinal fixo
Exemplos (continuação)
Exemplos
1
a) A sucessão de termo geral an = é decrescente pois
n
1
1
n − (n + 1)
−1
an+1 − an =
− =
=
60
n+1 n
n(n + 1)
n(n + 1)
c) Estudemos a natureza da série
n=1
an+1 − an =
1
1
=
= 0.
n→+∞
n→+∞ n
+∞
Pelo critério de Leibniz, a série
=
lim an = lim
=
+∞
X
(−1)n
n
n=1
=
6
Cálculo I
2010/2011
553 / 590
António Bento (UBI)
§6.2.3 Séries de termos sem sinal fixo
n+2 n+1
−
n+1
n
(n + 2)n − (n + 1)2
n(n + 1)
2
n + 2n − (n2 + 2n + 1)
n(n + 1)
−1
n(n + 1)
0
Cálculo I
2010/2011
555 / 590
§6.2.3 Séries de termos sem sinal fixo
Exemplos (continuação)
Exemplos (continuação)
+∞
X
(−1)n
b) Estudemos a natureza da série
. Como
n2
n=1
c) (continuação) No entanto, como
1
1
n − (n + 1)
n − (n + 2n + 1)
−2n − 1
− 2 =
=
= 2
60
(n + 1)2
n
n2 (n + 1)2
n2 (n + 1)2
n (n + 1)2
1
para qualquer n ∈ N, ou seja, a sucessão de termo geral an = 2 é
n
decrescente, e
1
1
1
lim
=
=
= 0,
2
n→+∞ n2
(+∞)
+∞
2
2
2
2
o critério de Leibniz garante-nos que a série
António Bento (UBI)
n+1
. A
n
para qualquer n ∈ N.
António Bento (UBI)
é convergente.
(−1)n an com an =
sucessão (an ) é decrescente pois
para qualquer n ∈ N. Além disso,
é convergente.
+∞
X
+∞
X
(−1)n
n2
n=1
Cálculo I
2010/2011
554 / 590
lim an = lim
n→+∞
n→+∞
n+1
n 1
1
= lim
+ = lim 1 + = 1,
n→+∞
n→+∞
n
n n
n
não podemos aplicar o critério de Leibniz pois
lim an 6= 0.
Mas se lim an = 1, a sucessão de termo geral (−1)n an é divergente
pois a subsucessão dos termos de ordem par converge para 1 e a
subsucessão dos termos de ordem ímpar converge para −1. Assim,
a série
+∞
+∞
X
X
n+1
é divergente.
(−1)n an =
(−1)n
n
n=1
n=1
António Bento (UBI)
Cálculo I
2010/2011
556 / 590
§6.2.3 Séries de termos sem sinal fixo
Uma série
módulos
+∞
X
§6.2.3 Séries de termos sem sinal fixo
Exemplos
an diz-se absolutamente convergente se a série dos
n=1
+∞
X
n=1
+∞
X
(−1)n
é
n2
n=1
convergente. Uma outra forma de vermos que é convergente é através da
série do módulos:
a) Através do critério de Leibniz concluímos que a série
|an | é convergente.
+∞ +∞
X
X
(−1)n 1
=
.
n2 2
n
n=1
n=1
As séries absolutamente convergentes são convergentes, ou seja, se
+∞
X
n=1
então
+∞
X
+∞
X
1
é uma série de Dirichlet com α = 2 e, portanto, é
n2
n=1
convergente. Logo
|an | é convergente,
Ora a série
+∞
X
(−1)n
n2
n=1
an também é convergente.
n=1
é absolutamente convergente e, portanto, é convergente.
António Bento (UBI)
Cálculo I
2010/2011
557 / 590
António Bento (UBI)
§6.2.3 Séries de termos sem sinal fixo
Cálculo I
559 / 590
§6.2.3 Séries de termos sem sinal fixo
Exemplos (continuação)
Observação
O recíproco do resultado anterior não se verifica. A série
+∞
X
n=1
b) Estudemos a natureza da série
(−1)n
n ∈ N, se tem
n
é convergente, mas a sua série dos módulos
+∞
X n=1
+∞
n X 1
(−1) =
n n
n=1
As séries convergentes cuja série dos módulos é divergente dizem-se
simplesmente convergentes, semi-convergentes ou
condicionalmente convergentes.
Cálculo I
2010/2011
558 / 590
0 6 +∞
X
cos n
. Como, para qualquer
2 + 2n + 3
n
n=1
cos n
|cos n|
1
1
=
6 2
6 2
2
n + 2n + 3 n2 + 2n + 3
n + 2n + 3
n
+∞
X
1
é convergente, pelo critério geral de comparação, a série
n2
n=1
+∞ X
cos n
n2 + 2n + 3 é convergente. Logo
n=1
e a série
é a série harmónica que já vimos ser divergente.
António Bento (UBI)
2010/2011
+∞
X
n=1
n2
cos n
+ 2n + 3
é absolutamente convergente e, por conseguinte, é convergente.
António Bento (UBI)
Cálculo I
2010/2011
560 / 590
§6.2.3 Séries de termos sem sinal fixo
§6.2.3 Séries de termos sem sinal fixo
Exemplos (continuação)
c) Consideremos a série
+∞
X
(−1)n
n=1
Para séries de termos sem sinal fixo também temos um critério de
d’Alembert e um de Cauchy.
n+1
. A sua série dos módulos é
n2 + 2
+∞ +∞
X
X
n+1
n n+1 (−1) 2
=
2
n +2
n=1
e, como
n=1
Critério de D’Alembert (para séries de termos sem sinal fixo)
n +2
Seja
n+1
2 +2
n2 (1 + 1/n)
1 + 1/n
n2 + n
n
lim
= lim
=
lim
= lim
= 1,
1
n→+∞
n→+∞ n2 + 2
n→+∞ n2 (1 + 2/n)
n→+∞ 1 + 2/n
n
+∞
+∞
X
X
n+1
1
e
, por serem séries de termos
pelo critério do limite, as séries
2
n +2
n
n=1
n=1
positivos, são da mesma natureza. Como a série harmónica é divergente, a série
X
an uma série de termos não nulos tal que
lim
a) Se λ < 1, então
b) Se λ > 1, então
+∞
X n+1
n=1
n2 + 2
X
X
|an+1 |
= λ.
|an |
an é absolutamente convergente.
an é divergente.
também é divergente.
António Bento (UBI)
Cálculo I
2010/2011
561 / 590
António Bento (UBI)
§6.2.3 Séries de termos sem sinal fixo
Cálculo I
2010/2011
563 / 590
§6.2.3 Séries de termos sem sinal fixo
Exemplos (continuação)
c) (continuação) Acabámos de ver que a série dos módulos de
+∞
X
(−1)n
n=1
+∞
divergente. Vejamos, usando o critério de Leibniz, que a série
X
n=1
convergente. Como
n+1
é
n2 + 2
n+1
(−1) 2
é
n +2
n
Critério de Cauchy (para séries de termos sem sinal fixo)
Seja
X
an uma série tal que
lim
n+1
n(1 + 1/n)
1 + 1/n
1+0
lim
= lim
= lim
=
=0
n→+∞ n2 + 2
n→+∞ n2 (1 + 2/n2 )
n→+∞ n(1 + 2/n2 )
+∞(1 + 0)
a) Se λ < 1, então
e
n+2
n+1
n2 + 3n − 1
− 2
= ··· = −
60
2
(n + 1) + 2
n +2
((n + 1)2 + 2)(n2 + 1)
para qualquer n ∈ N, pelo critério de Leibniz a série
+∞
X
(−1)n
n=1
b) Se λ > 1, então
X
X
q
n
|an | = λ.
an é absolutamente convergente.
an é divergente.
n+1
n2 + 2
é convergente. Assim, esta série é simplesmente convergente.
António Bento (UBI)
Cálculo I
2010/2011
562 / 590
António Bento (UBI)
Cálculo I
2010/2011
564 / 590
§6.3 Séries de potências
Índice
Observações
1
Funções reais de variável real: generalidades e exemplos
2
Funções reais de variável real: limites e continuidade
3
Cálculo diferencial em R
4
Primitivas
5
Cálculo integral em R
6
Sucessões e séries
Sucessões de números reais
Séries de números reais
Séries de potências
a) Há séries de potências que não começam em zero. Por exemplo, a série
+∞
+∞
X
1 n X xn
x =
n
n
n=1
n=1
tem de começar em um. Obviamente, tudo o que vamos estudar nesta
secção contínua válido para estas séries.
b) Uma série de potências pode convergir para determinados valores de x e
divergir para outros.
c) Quando x = a e n = 0 obtemos (x − a)n = 00 que, apesar de não estar
definido, no contexto das séries convencionamos ser igual a 1.
d) Para x = a, tendo em conta a observação c), a série é sempre convergente.
Aliás, se x = a temos
+∞
X
an (x − a)n = a0 .
n=0
António Bento (UBI)
Cálculo I
2010/2011
565 / 590
António Bento (UBI)
§6.3 Séries de potências
n=0
an (x − a)n
= a0 + a1 (x − a) + a2 (x − a)2 + · · · + an (x − a)n + · · ·
designa-se por série de potências de x − a. Dizemos que a série está
centrada em a e que os números an são os coeficientes da série.
xn
,
n!
n=0
n
(x − 2)n
2
n
+
1
n=0
e
+∞
X
n=0
n(x − π)n
Cálculo I
2010/2011
|x|n+1
1+
n + 2 = lim n + 1 |x| = lim
n→+∞ n + 2
n→+∞
|x|n
1+
n+1
1
n |x| = 1 . |x| = |x|
2
n
+∞
X
xn
é absolutamente convergente para |x| < 1 e
n+1
n=0
é divergente se |x| > 1.
e, portanto, a série
são séries de potências centradas, respectivamente, em 0, 2 e π.
António Bento (UBI)
+∞
X
xn
. Aplicando o critério de
n+1
n=0
D’Alembert à série dos módulos
+∞ +∞
n
X
X
xn |x|
=
n + 1
n+1
n=0
n=0
(quando x 6= 0) temos
a) Estudemos a série de potências
n→+∞
+∞
X
567 / 590
Exemplos de séries de potências
lim
As séries
+∞
X
2010/2011
§6.3 Séries de potências
Sejam a0 , a1 , . . . , an , . . . os termos de uma sucessão e a um número real.
A série
+∞
X
Cálculo I
566 / 590
António Bento (UBI)
Cálculo I
2010/2011
568 / 590
§6.3 Séries de potências
§6.3 Séries de potências
Exemplos de séries de potências (continuação)
Exemplos de séries de potências (continuação)
a) (continuação) Falta ver o que acontece quando |x| = 1. Se x = 1, então
obtemos a série
+∞
+∞
X
X
1
1
=
,
n
+
1
n
n=0
n=1
isto é, obtemos a série harmónica que já vimos ser divergente. Para
x = −1, temos a série alternada
n→+∞
que é convergente (ver os exemplos do critério de Leibniz). Assim, esta
série é convergente para x ∈ [−1, 1[ e é divergente para
x ∈ ] − ∞, −1[ ∪ [1, +∞[.
Cálculo I
2010/2011
569 / 590
+∞
X
n=0
lim
nxn . Aplicando o critério de Cauchy à
n=0
série dos módulos
temos
∞
∞
X
X
(−1)n
(−1)n+1
=
n+1
n
n=0
n=1
António Bento (UBI)
c) Estudemos a natureza da série
+∞
X
|nxn | =
+∞
X
n=0
n |x|n
q
√
n
n
n |x| = lim n n |x| = 1 . |x| = |x| .
n→+∞
Assim, a série é absolutamente convergente para |x| < 1. Para |x| > 1 a
série é divergente. Para |x| = 1 a série também é divergente. Portanto, a
série
+∞
X
nxn
n=0
converge se x ∈ ] − 1, 1[ e diverge se x ∈ ] − ∞, −1] ∪ [1, +∞[.
António Bento (UBI)
§6.3 Séries de potências
Cálculo I
2010/2011
571 / 590
§6.3 Séries de potências
Exemplos de séries de potências (continuação)
+∞ n
X
x
b) Consideremos a série de potências
. Aplicando o critério de
n!
n=0
D’Alembert à série dos módulos
+∞ n +∞
n
X
X
x |x|
=
n! n!
n=0
n=0
Sejam a0 , a1 , . . . , an , . . . os termos de uma sucessão e a um número
real. Então
a) existe um número real r > 0 tal que a série de potências
+∞
X
n=0
(para x 6= 0) tem-se
|x|n+1
n!
1
(n + 1)!
lim
= lim
|x| = lim
|x| = 0 · |x| = 0,
n→+∞
n→+∞ (n + 1)!
n→+∞ n + 1
|x|n
n!
+∞ n
X
x
o que permite concluir que a série
é absolutamente convergente
n!
n=0
para todo o x ∈ R.
António Bento (UBI)
Cálculo I
2010/2011
570 / 590
an (x − a)n
converge absolutamente quando |x − a| < r e diverge quando
|x − a| > r; ou
b) a série de potências
+∞
X
n=0
an (x − a)n
converge absolutamente para qualquer x ∈ R.
António Bento (UBI)
Cálculo I
2010/2011
572 / 590
§6.3 Séries de potências
§6.3 Séries de potências
O número r do resultado anterior designa-se por raio de
convergência da série de potências
+∞
X
n=0
an (x − a)n .
Observações (continuação)
Se estivermos no caso da alínea b) costuma-se fazer r = +∞.
b) De forma análoga prova-se, usando o critério de Cauchy, que se
O conjunto dos x para os quais a série é convergente designa-se por
intervalo de convergência da série de potências
+∞
X
n=0
lim
então
r=
Note-se que o intervalo de convergência de uma série de potências é um
dos quatro intervalos seguintes:
]a − r, a + r[ ,
[a − r, a + r[ ,
António Bento (UBI)
]a − r, a + r]
ou
Cálculo I
n
n→+∞
an (x − a)n .
q
|an | = λ,
1
1
= lim p
.
n
n→+∞
λ
|an |
[a − r, a + r] .
2010/2011
573 / 590
António Bento (UBI)
§6.3 Séries de potências
Cálculo I
2010/2011
575 / 590
§6.3 Séries de potências
Observações
|an+1 |
1
= λ, então r = .
n→+∞ |an |
λ
De facto, supondo x 6= a e an 6= 0 para qualquer n ∈ N, como
an+1 (x − a)n+1 |an+1 |
lim
= lim
|x − a| = λ |x − a| ,
n→+∞
n→+∞ |an |
|an (x − a)n |
a) Do critério de D’Alembert resulta que se lim
pelo critério de D’Alembert, a série é absolutamente convergente se
Além disso, se
1
λ |x − a| < 1 ⇔ |x − a| < .
λ
λ |x − a| > 1 ⇔ |x − a| >
1
,
λ
+∞
X
xn
e
n+1
n=0
provámos que o raio de convergência desta série é r = 1 e que o seu
intervalo de convergência é [−1, 1[.
a) Já estudamos a natureza da série de potências
b) Num exemplo anterior vimos o raio de convergência da série de
+∞
X xn
potências
é r = +∞ e, consequentemente, o seu intervalo de
n!
n=0
convergência é ] − ∞, +∞[= R.
c) Também já vimos que a série
a série é divergente. Logo
+∞
X
nxn tem como raio de
n=0
r=
António Bento (UBI)
Exemplos
convergência r = 1 e o seu intervalo de convergência é ] − 1, 1[.
1
|an |
= lim
.
λ n→+∞ |an+1 |
Cálculo I
2010/2011
574 / 590
António Bento (UBI)
Cálculo I
2010/2011
576 / 590
§6.3 Séries de potências
§6.3 Séries de potências
Exemplos (continuação)
Exemplos (continuação)
+∞
X
(x − 1)n
d) Estudemos a série de potências
. Consideremos a série
n2 2n
n=1
dos módulos
+∞
+∞
X (x − 1)n X |x − 1|n
=
n2 2n n2 2n
n=1
n=1
e apliquemos-lhe (para x 6= 1) o critério de D’Alembert
n+1
lim
n→+∞
|x − 1|
n2
2n |x − 1|n+1
(n + 1)2 2n+1
=
lim
n
n→+∞ (n + 1)2 2n+1 |x − 1|
|x − 1|n
n2 2n
1
|x − 1|
|x − 1|
= lim
=
.
n→+∞ (1 + 1/n)2
2
2
António Bento (UBI)
Cálculo I
2010/2011
577 / 590
d) (continuação) Quando x = 3 temos
+∞
+∞
+∞
X
X
X
(3 − 1)n
2n
1
=
=
2
n
2
n
n 2
n 2
n2
n=1
n=1
n=1
que é uma série de Dirichlet convergente. Quando x = −1 vem
+∞
+∞
+∞
+∞
X
X
X
X
(−1 − 1)n
(−2)n
(−1)n 2n
(−1)n
=
=
=
,
n2 2 n
n2 2 n
n2 2 n
n2
n=1
n=1
n=1
n=1
e esta série é convergente. Para vermos isso podemos usar o critério de
Leibniz ou então ver que a sua série dos módulos
+∞ +∞
+∞
X
X
(−1)n |(−1)n | X 1
=
=
n2 n2
n2
n=1
n=1
n=1
é convergente. Assim, o raio de convergência da série
e o seu intervalo de convergência é [−1, 3].
António Bento (UBI)
§6.3 Séries de potências
2010/2011
579 / 590
§6.3 Séries de potências
Exemplos (continuação)
Exemplos (continuação)
e) Consideremos a série de potências
+∞
X
(x − 1)n
d) (continuação) Assim, a série
é absolutamente
n2 2n
n=1
convergente quando
+∞
X
n=1
|x − 1|
< 1 ⇔ |x − 1| < 2 ⇔ x − 1 < 2 ∧ x − 1 > −2
2
⇔ x < 3 ∧ x > −1 ⇔ x ∈ ] − 1, 3[
n
(x − 2)n .
+1
n+1
|x − 2|n+1
n3 + n2 + n + 1
(n + 1)2 + 1
lim
= lim 3
|x − 2| = |x − 2|
n
n + 2n2 + 2n
n
|x
−
2|
n2 + 1
|x − 1|
> 1 ⇔ x ∈ ] − ∞, −1[ ∪ ]3, +∞[.
2
concluímos pelo critério de d’Alembert que se |x − 2| < 1, isto é, se
x ∈ ]1, 3[, a série converge absolutamente. Se |x − 2| > 1 a série diverge.
Falta ver o que acontece quando x = −1 e x = 3.
Cálculo I
n2
Para cada x ∈ R obtemos uma série numérica cuja série dos módulos
+∞
X
n
associada é
|x − 2|n , uma série de termos positivos. Como
2+1
n
n=1
e é divergente quando
António Bento (UBI)
Cálculo I
+∞
X
(x − 1)n
ér=2
n2 2 n
n=1
2010/2011
578 / 590
António Bento (UBI)
Cálculo I
2010/2011
580 / 590
§6.3 Séries de potências
§6.3 Séries de potências
Exemplos (continuação)
No intervalo de convergência I de uma série de potências
e) (continuação) Se x = 3, obtemos a série
+∞
X
+∞
X
+∞
X
n
n
n
(3
−
2)
=
,
2
2
n +1
n +1
n=1
n=1
n=0
que por ser uma série de termos positivos, estudaremos a sua natureza
recorrendo ao critério do limite, fazendo a comparação com a série
harmónica. Como
lim
an (x − a)n
fica bem definida a função f : I → R dada por
f (x) =
+∞
X
n=0
n/(n2 + 1)
n2
= lim 2
=1
1/n
n +1
an (x − a)n
= a0 + a1 (x − a) + a2 (x − a)2 + · · · + an (x − a)n + · · · .
concluímos que para x = 3 a série tem a mesma natureza da série
harmónica e, portanto, diverge.
António Bento (UBI)
Cálculo I
2010/2011
581 / 590
António Bento (UBI)
§6.3 Séries de potências
Propriedades da função f (x) =
e) (continuação) Além disso, se x = 1 obtemos a série
+∞
X
n=1
(−1)n
n2
n
. A
+1
n
sucessão de termo geral an = 2
é decrescente visto que
n +1
n+1
n
−n2 − n + 1
−
=
< 0 para todo o n ∈ N.
(n + 1)2 + 1 n2 + 1
(n2 + 2n + 2)(n2 + 1)
Seja
+∞
X
n=0
583 / 590
n
1
1
n
lim
= lim
= lim
=
=0
2
2
2
2
n→+∞ n + 1
n→+∞ n (1 + 1/n )
n→+∞ n(1 + 1/n )
+∞
podemos concluir pelo critério de Leibniz que, para x = 1, a série
converge. Assim, a série converge para x ∈ [1, 3[ e diverge para
x ∈ ] − ∞, 1[ ∪ [3 + ∞[.
2010/2011
P+∞
n=0
an (x − a)n
an (x − a)n
uma série de potências com raio de convergência r e com intervalo de
convergência I. Consideremos a função f : I → R definida por
Por outro lado, uma vez que temos
Cálculo I
2010/2011
§6.3 Séries de potências
Exemplos (continuação)
António Bento (UBI)
Cálculo I
f (x) =
+∞
X
n=0
an (x − a)n .
Então
a) a função f é contínua em I;
b) a função f é de classe C ∞ em ]a − r, a + r[;
582 / 590
António Bento (UBI)
Cálculo I
2010/2011
584 / 590
§6.3 Séries de potências
Propriedades da função f (x) =
P+∞
n=0
c) para cada x ∈ ]a − r, a + r[ tem-se
f ′ (x) =
+∞
X
n=0
§6.3 Séries de potências
an (x − a)n (continuação)
Exemplos
a) Seja f : R \ {1} → R a função dada por
[an (x − a)n ]′ ,
f (x) =
Quando estudámos a série geométrica vimos que para cada
x ∈ ] − 1, 1[ temos
ou seja,
f ′ (x) =
+∞
X
n=1
=
+∞
X
nan (x − a)n−1
+∞
X
(n + 1)an+1 (x − a)
n=0
= a1 + 2a2 (x − a) + 3a3 (x − a)2 + · · · + nan (x − a)n−1 + · · ·
Cálculo I
2010/2011
585 / 590
Propriedades da função f (x) =
P+∞
n=0
d) para cada x ∈ ]a − r, a + r[ tem-se
f (x) dx =
" +∞
X
an
n=0
a)n+1
(x −
n+1
#
António Bento (UBI)
an (x − a)n (continuação)
2010/2011
587 / 590
Exemplos (continuação)
b) Como
+C
1
1−x
′
=
1′ (1 − x) − 1(1 − x)′
0(1 − x) − 1(−1)
1
=
=
,
(1 − x)2
(1 − x)2
(1 − x)2
usando o exemplo anterior e uma das propriedades anteriores,
temos, para x ∈] − 1, 1[,
1
=
(1 − x)2
ou seja, a função g dada por
+∞
X
(x − a)n+1
g(x) =
an
n+1
n=0
=
1
1−x
+∞
X
′
2010/2011
586 / 590
António Bento (UBI)
=
nxn−1 =
n=1
é uma primitiva de f .
Cálculo I
Cálculo I
§6.3 Séries de potências
a1
a2
= C + a0 (x − a) + (x − a)2 + (x − a)3 + · · · +
2
3
an
n+1
(x − a)
+
+ ···
n+1
António Bento (UBI)
1
= f (x).
1−x
Verificamos então que f admite um desenvolvimento em série de
potências de x no intervalo ] − 1, 1[.
§6.3 Séries de potências
Z
xn =
n=0
n
António Bento (UBI)
1
.
1−x
Cálculo I
+∞
X
(xn )′
n=0
+∞
X
(n + 1)xn
n=0
2010/2011
588 / 590
§6.3 Séries de potências
Exemplos (continuação)
c) O estudo que fizemos da série geométrica permite-nos concluir,
para cada x ∈ ] − 1, 1[, que
+∞
+∞
X
X
1
1
=
=
(−x)n =
(−1)n xn .
1+x
1 − (−x) n=0
n=0
1
tem-se
1+x
+∞
X
xn+1
ln(1 + x) = C +
(−1)n
n+1
n=0
Como ln(1 + x) é uma primitiva de
para algum C ∈ R. Como ln(1 + 0) = 0, tem-se C = 0 e, por
conseguinte,
ln(1 + x) =
+∞
X
(−1)n
n=0
António Bento (UBI)
xn+1
para qualquer x ∈ ] − 1, 1[.
n+1
Cálculo I
2010/2011
589 / 590
§6.3 Séries de potências
Exemplos (continuação)
d) Usando novamente a série geométrica, para x ∈ ] − 1, 1[, temos
+∞
+∞
X
X
1
1
2 n
=
=
(−x
)
=
(−1)n x2n
1 + x2
1 − (−x2 ) n=0
n=0
e, pelas propriedades estudadas, tem-se para x ∈ ] − 1, 1[
arc tg x = C +
+∞
X
(−1)n
n=0
x2n+1
2n + 1
para algum C ∈ R. Como arc tg 0 = 0, concluímos que C = 0 e,
portanto,
arc tg x =
+∞
X
(−1)n
n=0
António Bento (UBI)
x2n+1
para x ∈ ] − 1, 1[.
2n + 1
Cálculo I
2010/2011
590 / 590