1aExperiencia- Equipotenciais Arquivo

Física III – Prática Vinculada (5910233)
1ª. Experiência
Linhas Equipotenciais
Objetivos
Mapeamento das linhas equipotenciais produzidos por diferentes geometrias de
carga elétrica.
O conceito de campo
O conceito de campo é bastante geral e pode ser aplicado a diversas grandezas.
Um campo é uma região do espaço onde alguma grandeza tem um valor definido em
todos os pontos. Podemos falar no campo gravitacional terrestre que faz com que a toda
cota H esteja associada uma determinada aceleração da gravidade g. A meteorologia
pode fornecer dados como na figura 1, onde são mostradas a temperatura e pressão num
determinado dia. Como tanto pressão quanto temperatura são grandezas escalares este
campo é um campo escalar.
Ao examinar uma carta metereológica podemos encontrar uma maneira mais
prática de mostrar esses dados da figura 1 como ilustrado na figura 2. Neste caso foi
feito um "ajuste" dos dados por meio de linhas contínuas e temos as isobáricas e
isotermas, como se percebe fica mais fácil visualizar a informação neste último caso.
Suponhamos que agora os metereologistas mediram a velocidade do vento.
Como representar esta grandeza? Uma possibilidade é mostrada na figura 3, onde cada
seta indica a direção e sentido do vento e o comprimento representa o valor da
velocidade. Neste caso como a velocidade é uma grandeza vetorial e temos na figura 3
um campo vetorial.
Figura 1 - Temperatura e pressão em diferentes pontos.
Física III – Prática Vinculada (5910233)
1ª. Experiência
Figura 2 - Linhas isobáricas e isotermas
Figura 3 - Distribuição da velocidade do vento
Força, campo e potencial elétrico
Suponhamos que temos uma partícula positivamente carregada no vácuo e queremos
conhecer suas características elétricas. Alguma forma tem que ser encontrada para
interagir com esta partícula e a maneira mais simples é nos valermos de uma outra carga
positiva, que será chamada de carga de prova, e pesquisar as relações com a carga
inicial. A grandeza mais facilmente mensurável neste caso é a força de interação que
sabemos ser proporcional às cargas e inversamente proporcional ao quadrado da
distância de separação e na direção do vetor que une as duas cargas, isto é:

F 1, 2

1
Q1 Q2
4  0
r12, 2

r1, 2
Podemos então descrever a partícula carregada em termos da força que seria
exercida sobre uma carga de prova em qualquer ponto do espaço, a forma de visualizar
isto seria através de linhas de força, que são tangentes à força em cada ponto do espaço.
Um conceito que está intimamente ligado ao de força elétrica é o de campo elétrico,
operacionalmente define-se o campo elétrico como,
Física III – Prática Vinculada (5910233)

E1 
1ª. Experiência

F 1, 2
Q2

1
4  0
Q1 
r,
r2
portanto o campo elétrico é um vetor paralelo à força, porém com módulo Q2 vezes
menor.
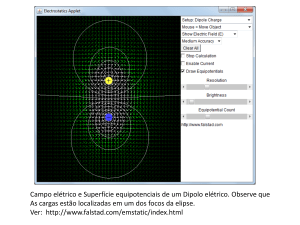
A figura 4 mostra as linhas de campo elétrico de uma carga pontual +Q, -Q e
+2Q. Observe que a densidade de linhas de campo é proporcional à intensidade da
carga elétrica.
B
-
+
-q
-q
A
A
+2
+ 2q
Figura 4 - Linhas de campo elétrico para diferentes cargas elétricas
Agora que temos uma visão das linhas de campo elétrico podemos fazer a
seguinte pergunta: um agente externo realiza algum trabalho quando leva a carga de A
até B pelo trajeto indicado na figura 4? A resposta é não, pois a força eletrostática,


F  q E , é perpendicular à trajetória e consequentemente não existe trabalho realizado
sobre o sistema e nem variação da energia potencial U. Portanto uma carga de prova
colocada em qualquer ponto de um círculo concêntrico com a carga inicial possui a
mesma energia potencial U, o que equivale dizer que este círculo é uma curva
equipotencial pois o potencial é obtido através de V=U/q. Um ponto a se ressaltar é que
o conhecimento do campo elétrico implica no conhecimento das linhas equipotenciais e
vice-versa, e que ambas são perpendiculares entre si.
Materiais e métodos
Experimentalmente determinamos as superfícies equipotenciais de uma dada
geometria de cargas e depois encontramos as linhas de campo elétrico. O problema
experimental consiste em como encontrar essas superfícies ou linhas equipotenciais.
Uma maneira prática é utilizarmos um aparelho (voltímetro ou galvanômetro)
que mede a diferença de potencial ou ddp e procurarmos os pontos que não possuem
ddp entre si (ddp=0 V) e assim determinamos as várias linhas equipotenciais. Para
facilitar o nosso trabalho essas medições serão realizadas numa solução eletrolítica de
CuSO4 na qual estão imersos eletrodos simulando a distribuição de cargas que vamos
mapear as equipotenciais. A figura 5 ilustra o arranjo experimental a ser montado.
Física III – Prática Vinculada (5910233)
1ª. Experiência
ponta fixa
ponta móvel
CuSO4
eletrodos
Papel milimetrado
Figura 5 – Arranjo experimental para a determinação de linhas equipotenciais com os
dois eletrodos cilíndricos.
Os materiais utilizados são uma fonte de alimentação, uma cuba, uma solução de
CuSO4 (sulfato de cobre), fios de conexão, pontas de prova, um galvanômetro, papel
milimetrado com as posições dos eletrodos marcados, eletrodos metálicos e um
voltímetro (não representado na figura 5).
Procedimento experimental
1. Insira o papel milimetrado com as marcações circulares (que representam as
posições dos eletrodos cilíndricos) na “gaveta” da cuba, e posicione os eletrodos
cilíndricos sobre as marcações.
2. Conecte a alimentação da fonte (com 1V ajustado) nos eletrodos cilíndricos, e as
pontas de prova do galvanômetro (+ e -) respectivamente nas pontas móvel e
fixa, conforme figura 5.
3. Você dispõe de duas folhas de papel milimetrado de cada configuração
mostradas na figura 6. Uma foi inserida na cuba e sobre a outra será feito o
“mapeamento” das linhas equipotenciais a lápis ponto a ponto.
Física III – Prática Vinculada (5910233)
1ª. Experiência
Figura 6 – Modelos de papel milimetrado mostrando as posições em que devem ser
posicionados os eletrodos. (a) dois cilindros; (b) duas barras; (c) barra e cilindro; (d)
barra – anel – barra.
4. Posicione a ponta móvel 1 cm à frente do eletrodo (neste 1º caso, o cilíndrico), e
em seguida procure com a ponta fixa onde o galvanômetro “zera” (isto indicará
que você posicionou a ponteira fixa sobre um ponto da mesma linha
equipotencial que passa 1 cm à frente do eletrodo).
5. Faça uma marcação nos pontos em que estão posicionados as ponteiras fixa
(também chamada de referência) e móvel (ex: D23: posição da ponta de
referência como mostrado na figura 7).
Física III – Prática Vinculada (5910233)
1ª. Experiência
Figura 7 – Cuba vista de cima, mostrando os eletrodos, as pontas fixa (posição D23) e
móvel (posição K20) a 1 cm do eletrodo, o papel milimetrado imerso no CuSO4 e o
galvanômetro à esquerda.
6. Em seguida desloque a ponteira fixa 2cm para baixo (o galvanômetro mostrará
um valor ≠ 0, pois você saiu da linha equipotencial na qual ainda permanece a
referência), então desloque um pouco para a direita ou para a esquerda a ponteira
móvel até encontrar a posição onde o galvanômetro zera novamente (o que
significa que você encontrou outro ponto dentro da mesma linha equipotencial
em que estava) e faça mais uma marcação na folha de papel milimetrado.
7. Repita os procedimentos 5 e 6 para mais 4 pontos acima e abaixo do ponto
inicial (ponta móvel 1 cm à frente do eletrodo feito no item 4) fazendo sempre
uma marcação no papel milimetrado referente à posição em que o galvanômetro
zera.
8. Com o voltímetro, verifique a diferença de potencial entre a linha equipotencial
que você traçou e o eletrodo. Faça isso colocando uma ponteira do voltímetro
sobre o eletrodo e a outra sobre a referência em que se está traçando a linha
equipotencial.
9. Encontre mais 3 linhas equipotenciais como esta repetindo os procedimentos
anteriores começando pelo posicionamento da ponta móvel à frente do eletrodo
em outras três posições (2, 3 e 4 cm) e zerando o galvanômetro com a ponta fixa
para cada nova linha equipotencial encontrada.
10. Repita os procedimentos de 4 a 9 para o outro eletrodo (neste 1º caso, cilíndrico
também) e verifique a simetria presente nesta configuração.
11. Repita os procedimentos de 1 a 10 para as outras configurações mostradas na
figura 6.
Bibliografia
TIPLER, P. A. O potencial elétrico. In: ______. Física para cientistas e engenheiros:
Eletricidade e magnetismo, ótica. 4 ed. Rio de Janeiro: LTC, 2000. v. 2. p. 60-86.