Visualizando o volume molar

Visualizando o volume molar
Experimento cadastrado por Leandro Fantini em 17/03/2009
Classificação
•••••
(baseado em 7 avaliações)
Total de exibições: 4864 (até 10/06/2013)
Palavras-chave: Química, Mol, gás, partículas, volume molar,
PV=nRT
Onde encontrar o material?
em supermercados e farmácias
Quanto custa o material?
até 10 reais
Tempo de apresentação
até 10 minutos
Dificuldade
fácil
Segurança
seguro
Introdução
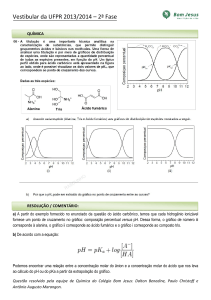
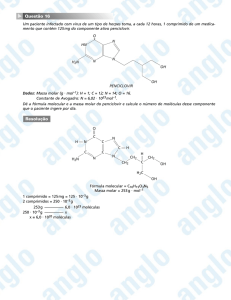
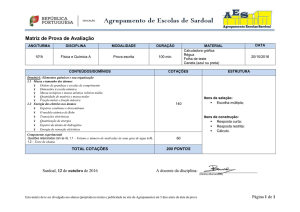
Construa você mesmo uma estrutura que permite enxergar o volume de um mol de gás nas CNTP.
Estrutura cúbica com 22,4 litros
Materiais necessários
Oito bolinhas de isopor com 3cm de diâmetro
Doze espetos de churrasco ou taquaras com 28,2cm de comprimento
OBS. Nós encontramos espetos de bambu para churrasco com o tamanho exato
© 2013 pontociência / www.pontociencia.org.br
1
Visualizando o volume molar
Material utilizado
Passo 1
Mãos à obra
Segure firmemente a bolinha de isopor com uma das mãos e com a outra introduza o espeto até a metade da bolinha
Passo 2
Mãos à obra
Faça uma base com quatro bolinhas de isopor e quatro espetos.
Logo em seguida, monte a estrutura cúbica como está na foto.
© 2013 pontociência / www.pontociencia.org.br
2
Visualizando o volume molar
Passo 3
O que acontece
Ao se mencionar o volume molar de gases é interessante demonstrar visualmente o que são 22,4 L como parte da discussão.
Para entendermos o porque deste volume, vamos recorrer a equação de Clapeyron.
PV = nRT onde,
P = Pressão
V = Volume
n = N° de mols
R = constante universal dos gases
T = Temperatura em Kelvin
Se você está utilizando a pressão em atm, o valor para R será de 0,082 atm.L / mol.K
Lembre-se que na CNTP ( condições normais de temperatura e pressão ), a pressão deve ser de 1 atm e a temperatura será
de 273,15 K ou 0°C. Como o valor de R está em Kelvin, vamos usar a temperatura nesta unidade.
Sendo assim veja como ficará nosso cálculo:
PV = nRT
> 1atm. V = 1mol. 0,082atm.L / mol.K . 273,15K
V = 22,4 L
Outro valor utilizado para o Volume Molar de um gás é o calculado nas CPTP ou Condições Padrão de Temperatura e
Pressão. Neste caso o que muda é apenas a unidade da pressão, que ao invés de ser dada em atmosferas é dada em Pascal
(Pa).
P = 100.000 Pa e T = 273,15 K - CPTP
Volume Molar = 22,7 L
Agora, porque o tamanho do espeto tem que ser de 28,2cm?
O volume de um cubo é: Base x Altura
© 2013 pontociência / www.pontociencia.org.br
3
Visualizando o volume molar
Sua base é comprimento x largura. Como todas as arestas (laterais), que chamaremos apenas de "a" são do mesmo tamanho
teremos o volume como:
a x a x a = a3
28,2cm x 28,2cm x 28,2cm = 22430 cm3
Lembrando também que 1 cm3 = 1 ml, temos que 22430cm3 = 22430mL, ou 22,4 litros, que é a mesma coisa. Por isso
utilizamos 28,2 cm como o tamanho do espeto.
Passo 4
Para saber mais
Clapeyron foi um engenheiro e físico francês que fez contribuições significativas por volta do ano de 1830, ao que hoje
conhecemos como a termodinâmica.
Baseando-se nas leis experimentais de Boyle, Charles, Gay-Lussac e Avogadro, Clapeyron propôs relações entre as variáveis
de estado de um gás, chegando então a já mencionada equação de Clapeyron, também conhecida como a equação de estado
dos gases perfeitos (ideais):
PV = nRT
Vale lembrar que esse valor é válido para uma atmosfera e 273,15K. Todos nós sabemos que se um gás for comprimido seu
volume diminuirá, porém a pressão não será mais de 1 atm, logo o valor do volume não será mais 22,4L. Você perceberá
também uma variação deste volume, caso a temperatura não seja de 273,15K. Por exemplo, para 25°C ou 298,15K o volume
de um mol de gás será de 24,4 litros.
© 2013 pontociência / www.pontociencia.org.br
Powered by TCPDF (www.tcpdf.org)
4