1° ano: Recuperação 3° Bimestre

Professor:
Física
SÉRIE: 1° ANO
LUTIANO
DATA: 10/ 10 / 2016
Recuperação - 3º Bimestre
Conteúdo:
Dinâmica do Movimento Circular
Refração da Luz
a) 6 km h.
b) 12 km h.
c) 21,6 km h.
d) 15 km h.
1. (Unesp) Num sistema massa-mola, conforme a figura
(superfície horizontal sem atrito) onde k é a constante elástica
da mola, a massa é 1. (Unesp) No "globo da morte", um
clássico do espetáculo circense, a motocicleta passa num
determinado instante pelo ponto mais alto do globo, como
mostra a figura adiante.
Supondo que, nesse trecho, a trajetória é circular e o módulo da
velocidade é constante, no sentido anti-horário, indique a
alternativa que apresenta corretamente a direção e sentido da
força resultante que atua sobre a motocicleta nesse ponto.
e) 18 km h.
3. (Epcar (Afa) 2015) Uma determinada caixa é transportada
em um caminhão que percorre, com velocidade escalar
constante, uma estrada plana e horizontal. Em um determinado
instante, o caminhão entra em uma curva circular de raio igual a
51,2 m, mantendo a mesma velocidade escalar. Sabendo-se
que os coeficientes de atrito cinético e estático entre a caixa e o
assoalho horizontal são, respectivamente, 0,4 e 0,5 e
considerando que as dimensões do caminhão, em relação ao
raio da curva, são desprezíveis e que a caixa esteja apoiada
apenas no assoalho da carroceria, pode-se afirmar que a
máxima velocidade, em m / s, que o caminhão poderá
desenvolver, sem que a caixa escorregue é
a) 14,3
b) 16,0
c) 18,0
d) 21,5
2. (G1 - ifce 2016) Considere a figura a seguir, na qual é
mostrado um piloto acrobata fazendo sua moto girar por dentro
de um “globo da morte”.
4. (Udesc 2011) Considere o “looping” mostrado na Figura,
constituído por um trilho inclinado seguido de um círculo.
Quando uma pequena esfera é abandonada no trecho inclinado
do trilho, a partir de determinada altura, percorrerá toda a
trajetória curva do trilho, sempre em contato com ele.
Sendo v a velocidade instantânea e a a aceleração centrípeta
da esfera, o esquema que melhor representa estes dois vetores
no ponto mais alto da trajetória no interior do círculo é:
Ao realizar o movimento de loop dentro do globo da morte (ou
seja, percorrendo a trajetória ABCD mostrada acima), o piloto
precisa manter uma velocidade mínima de sua moto para que a
mesma não caia ao passar pelo ponto mais alto do globo (ponto
“A”).
Nestas condições, a velocidade mínima “v” da moto, de forma
que a mesma não caia ao passar pelo ponto “A”, dado que o
globo da morte tem raio R de 3,60 m, é
(Considere g = 10 m/s2)
a)
b)
c)
d)
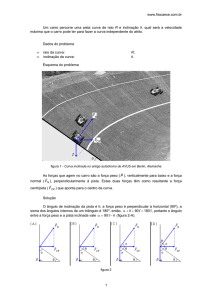
5. (Unesp) Curvas com ligeiras inclinações em circuitos
automobilísticos são indicadas para aumentar a segurança do
carro a altas velocidades, como, por exemplo, no Talladega
Superspeedway, um circuito utilizado para corridas promovidas
pela NASCAR (National Association for Stock Car Auto Racing).
Considere um carro como sendo um ponto material percorrendo
uma pista circular, de centro C, inclinada de um ângulo α e
8. (G1 - ifba 2014) Muitos parques de diversão se utilizam de
princípios físicos para seu completo funcionamento. O “chapéu
mexicano”, por exemplo, é um brinquedo no qual o indivíduo
fica girando sentado em uma cadeira pendurada por uma
corrente de 5 metros de comprimento a uma velocidade de
12,1m / s.
com raio R, constantes, como mostra a figura, que apresenta a
frente do carro em um dos trechos da pista.
Se a velocidade do carro tem módulo constante, é correto
afirmar que o carro
a) não possui aceleração vetorial.
b) possui aceleração com módulo variável, direção radial e no
sentido para o ponto C.
c) possui aceleração com módulo variável e tangente à
trajetória circular.
d) possui aceleração com módulo constante, direção radial e no
sentido para o ponto C.
e) possui aceleração com módulo constante e tangente à
trajetória circular.
6. (Puccamp)
Num trecho retilíneo de uma pista de
automobilismo há uma lombada cujo raio de curvatura é de
50 m. Um carro passa pelo ponto mais alto da elevação com
velocidade v, de forma que a interação entre o veículo e o solo
(peso aparente) é
Considerando
que
o
valor
da
gravidade
local
seja
g  9,8 m / s2 , podemos afirmar que as pessoas que andam
no chapéu mexicano ficam submetidas a uma aceleração
centrípeta de aproximadamente
a) g
b) 2g
c) 3g
d) 5g
e) 10g
9. (Fuvest 2013) O pêndulo de um relógio é constituído por
uma haste rígida com um disco de metal preso em uma de suas
extremidades. O disco oscila entre as posições A e C, enquanto
a outra extremidade da haste permanece imóvel no ponto P. A
figura abaixo ilustra o sistema. A força resultante que atua no
disco quando ele passa por B, com a haste na direção vertical,
é
mg
neste ponto. Adote g = 10 m/s2.
5
Nestas condições, em m/s, o valor de v é
a) 10
b) 20
c) 30
d) 40
e) 50
7. (Pucsp)
(Note e adote: g é a aceleração local da gravidade.)
a) nula.
b) vertical, com sentido para cima.
c) vertical, com sentido para baixo.
d) horizontal, com sentido para a direita.
e) horizontal, com sentido para a esquerda.
10. (Esc. Naval 2013) Um pêndulo, composto de um fio ideal
de comprimento L  2,00 m e uma massa M  20,0 kg,
A figura representa em plano vertical um trecho dos trilhos de
uma montanha russa na qual um carrinho está prestes a
realizar uma curva. Despreze atritos, considere a massa total
dos ocupantes e do carrinho igual a 500 kg e a máxima
velocidade com que o carrinho consegue realizar a curva sem
perder contato com os trilhos igual a 36 km/h. O raio da curva,
considerada circular, é, em metros, igual a
a) 3,6
b) 18
c) 1,0
d) 6,0
e) 10
executa um movimento vertical de tal forma que a massa M
atinge uma altura máxima de 0,400 m em relação ao seu
nível mais baixo. A força máxima, em newtons, que agirá no fio
durante o movimento será
2
Dado: g  10,0 m s
a) 280
d) 80,0
2
b) 140
e) 60,0
c) 120
11. (Pucsp) Um automóvel de massa 800 kg, dirigido por um
motorista de massa igual a 60 kg, passa pela parte mais baixa
de uma depressão de raio = 20 m com velocidade escalar de 72
km/h. Nesse momento, a intensidade da força de reação que a
pista aplica no veículo é: (Adote g = 10m/s 2).
13. (Fmp 2014)
a) 231512 N
b) 215360 N
c) 1800 N
d) 25800 N
e) 24000 N
A figura acima ilustra um raio monocromático que se propaga
no ar e incide sobre uma lâmina de faces paralelas, delgada e
de espessura d com ângulo de incidência igual a 60 . O raio
sofre refração, se propaga no interior da lâmina e, em seguida,
volta a se propagar no ar.
Se o índice de refração do ar é 1, então o índice de refração do
material da lâmina é
12. (Espcex (Aman) 2015) Uma fibra óptica é um filamento
flexível, transparente e cilíndrico, que possui uma estrutura
simples composta por um núcleo de vidro, por onde a luz se
propaga, e uma casca de vidro, ambos com índices de refração
diferentes.
Um feixe de luz monocromático, que se propaga no interior do
núcleo, sofre reflexão total na superfície de separação entre o
núcleo e a casca segundo um ângulo de incidência á, conforme
representado no desenho abaixo (corte longitudinal da fibra).
a)
6
3
b)
6
2
d)
6
e)
3
2
2
14. (G1 - ifpe 2014) Quando olhamos uma piscina, estando em
pé e do lado de fora da mesma, sempre temos a impressão de
que ela tem uma profundidade diferente da que percebemos
quando nela mergulhamos. Isso se deve ao fato de que o ar
atmosférico e a água têm índices de refração absolutos
diferentes. Se a profundidade real de uma piscina é 2,0 m e os
índices de refração absolutos do ar atmosférico e da água da
piscina valem 1,0 e 1,3, respectivamente, é correto dizer que
um observador em pé, fora da piscina, verá que a sua
profundidade será, aproximadamente, em metros:
a) 1,5
Com relação à reflexão total mencionada acima, são feitas as
afirmativas abaixo.
c)
b) 1,2
c) 2,4
d) 2,6
e) 1,0
15. (Mackenzie 2014) Certa piscina contém água, de índice de
refração absoluto igual a 4 3, e sua base se encontra 3,00 m
abaixo da superfície livre.
I. O feixe luminoso propaga-se do meio menos refringente para
o meio mais refringente.
II. Para que ela ocorra, o ângulo de incidência α deve ser
inferior ao ângulo limite da superfície de separação entre o
núcleo e a casca.
III. O ângulo limite da superfície de separação entre o núcleo e
a casca depende do índice de refração do núcleo e da
casca.
IV. O feixe luminoso não sofre refração na superfície de
separação entre o núcleo e a casca.
Dentre as afirmativas acima, as únicas corretas são:
a) I e II
b) III e IV
c) II e III
d) I e IV
e) I e III
Quando uma pessoa, na beira da piscina, olha
perpendicularmente para seu fundo (base), terá a impressão de
vê-lo
Dado: Índice de refração absoluto do ar n  1
a) 2,25 m mais próximo, em relação à profundidade real.
b) 1,33 m mais próximo, em relação à profundidade real.
c) 0,75 m mais próximo, em relação à profundidade real.
d) 1,33 m mais distante, em relação à profundidade real.
e) 0,75 m mais distante, em relação à profundidade real.
3
16. (Pucrj 2012) Um feixe luminoso se propagando no ar incide
em uma superfície de vidro. Calcule o ângulo que o feixe
refratado faz com a normal à superfície sabendo que o ângulo
de incidência θ i é de 60° e que os índices de refração do ar e
do vidro, ηar e ηvidro, são respectivamente 1,0 e
3.
18. (Ufpa 2011) Os índios amazônicos comumente pescam
com arco e flecha. Já na Ásia e na Austrália, o peixe arqueiro
captura insetos, os quais ele derruba sobre a água, acertandoos com jatos disparados de sua boca. Em ambos os casos a
presa e o caçador encontram-se em meios diferentes. As
figuras abaixo mostram qual é a posição da imagem da presa,
conforme vista pelo caçador, em cada situação.
a) 30°
b) 45°
c) 60°
d) 73°
e) 90°
17. (Fuvest 2012)
Identifique, em cada caso, em qual dos pontos mostrados, o
caçador deve fazer pontaria para maximizar suas chances de
acertar a presa.
Uma fibra ótica é um guia de luz, flexível e transparente,
cilíndrico, feito de sílica ou polímero, de diâmetro não muito
maior que o de um fio de cabelo, usado para transmitir sinais
luminosos a grandes distâncias, com baixas perdas de
intensidade. A fibra ótica é constituída de um núcleo, por onde
a luz se propaga e de um revestimento, como esquematizado
na figura acima (corte longitudinal). Sendo o índice de refração
do núcleo 1,60 e o do revestimento, 1,45, o menor valor do
ângulo de incidência  do feixe luminoso, para que toda a luz
incidente permaneça no núcleo, é, aproximadamente,
Note e adote
 (graus) sen 
25
0,42
30
0,50
45
0,71
50
0,77
55
0,82
60
0,87
65
0,91
a) Homem em A; peixe arqueiro em 1
b) Homem em A; peixe arqueiro em 3
c) Homem em B; peixe arqueiro em 2
d) Homem em C; peixe arqueiro em 1
e) Homem em C; peixe arqueiro em 3
cos 
0,91
0,87
0,71
0,64
0,57
0,50
0,42
n1 sen 1  n2 sen 2
a) 45º.
b) 50º.
c) 55º.
d) 60º.
e) 65º.
4
Gabarito
Resposta da questão 1:
[A]
Resposta da questão 2:
[C]
A velocidade mínima ocorre quando a força normal atuante na
moto for nula, sendo a resultante centrípeta o próprio peso.
Assim:
m v2
 mg  v
R
Rcent  P 
R g  3,6  10  6 m/s 
v  21,6 km/h.
tg α 
R c m  ac

 ac  g  tgα. Como α e g são
P
mg
Resposta da questão 3:
[B]
constantes, a aceleração centrípeta (radial, dirigida para o
centro) tem módulo constante.
No movimento circular uniforme, a resultante das forças radiais
é a força centrípeta:
Resposta da questão 6:
[B]
Fr  Fc 
m  v2
R
No ponto mais alto, a força centrípeta é a diferença entre o
peso e a normal.
A única força radial é a força de atrito que, dependendo da
velocidade, impede que a caixa seja deslocada dentro do
caminhão, sendo a resultante centrípeta.
m
V2
V2
mg 4mg
 mg  N  m
 mg 

 V 2  400  V  20m / s
R
50
5
5
Fr  Fat  μ  N 
 Fat  μ  m  g
Resposta da questão 7:
[E]
Igualando as duas equações:
Resposta da questão 8:
[D]
horizontal
m  v2
 μ mg
R
Isolando v:
v  μ R  g
Calculando o raio (R) da trajetória:
R2  42  52  R  3 m.
Fazendo a relação entre a aceleração centrípeta e a gravidade:
Substituindo os valores, temos a velocidade máxima para a
caixa não escorregar na carroceria:
v  0,5  51,2  10  256  16 m / s
Resposta da questão 4:
[A]
A figura mostra a velocidade tangencial da esfera e as forças
atuantes. A resultante será para baixo e a aceleração também.
2
2
12,1
ac v R
3  48,8  ac  5 


g
g
9,8
9,8
g
ac  5 g.
Resposta da questão 9:
[B]
No ponto considerado (B), a componente tangencial da
resultante é nula, restando apenas a componente centrípeta,
radial e apontando para o centro da curva (P). Portanto, a força
resultante tem direção vertical, com sentido para cima.
Resposta da questão 10:
[A]
Resposta da questão 5:
[D]
Conforme o diagrama anexo, as forças que agem no carro são
o peso (P) e a normal (N). Como o movimento é circular e
uniforme, a resultante dessas forças é centrípeta (radial), (RC ).
Para calcularmos a tração máxima no fio usaremos a dinâmica
do movimento circular:
(1)
Fc  Tmáx  P
v
Sabendo que: Fc  m máx
R
2
e P  mg
2
v
Tmáx  Fc  P  Tmáx  m máx  mg
R
5
(2)
Da conservação de energia, tiramos o valor de vmáx
Resposta da questão 13:
[B]
A figura mostra os ângulos de incidência e refração:
Nessa figura:
EM(A)  EM(B)
mgh 
2
m vmáx
2
tg r 
2
 vmáx
 2gh
(3)
d
 1  r  45.
d
Aplicando a lei de Snell:
nar sen i  n L sen r  1 sen 60  n L sen 45 
Substituindo (3) em (2):
2gh
20  2  10  0,4
 mg  Tmáx 
 20  10
R
2
Tmáx  280 N
nL 
Tmáx  m
Resposta da questão 11:
[D]
3
2
 nL
2
2
 nL 
3
2

6
.
2
Resposta da questão 14:
[A]
Considerando que o observador esteja olhando verticalmente
para baixo, temos:
di
do

nar
náb

di
1
2,0

 di 
 1  d i  1,54 m 
2 1,3
1,3
di  1,5 m.
Resposta da questão 15:
[C]
Aplicando a equação do dioptro plano, Calculamos a
profundidade aparente (hi ) da piscina para essa pessoa.
Dados: r = 20 m; v = 72 km/h = 20 m/s; m = (800 + 60) = 860 kg
e g = 10 m/s2.
Sendo FN a força de reação da pista e P o peso do conjunto,
analisando a figura, temos que a resultante centrípeta é:
RC = FN – P  FN = RC + P  FN =
h i nar

h o nág

hi
1

3 4
3
 h i  2,25 m.
Portanto, a imagem é sobrelevada de 0,75 m.
Resposta da questão 16:
m v2
860 (20)2
[A]
 m g  FN 
 860 (10)  17.200  8.600 
r
20
Aplicando a lei de Snell:
nar sen θ1  nvidro sen r  1 sen 60  3 sen r 
FN = 25.800 N.
3
1
 3 sen r  sen r 

2
2
r  30
Resposta da questão 12:
[B]
Resposta da questão 17:
[E]
[I] Incorreta. Para ocorrer reflexão total, a primeira condição é
que o sentido de propagação da luz seja do meio mais
refringente para o menos refringente.
[II] Incorreta. Para ocorrer reflexão total, a segunda condição é
que o ângulo de incidência no meio mais refringente seja
maior que o ângulo limite.
[III] Correta. A expressão do ângulo limite (L) é:
n
L  arc sen menor
nmaior
n
 L  arc sen casca .
nnúcleo
Basta calcularmos o ângulo limite, que é o ângulo de incidência
(  ) no meio mais refringente (núcleo) que provoca uma
emergência rasante (90°) no meio menos refringente
(revestimento).
Dados: nnúcleo = 1,60; nrevest = 1,45.
Aplicando a lei de Snell:
nnúcleo sen  nrevest sen90  sen 
nresvest 1,45

nnúcleo 1,60
Consultando a tabela dada:  = 65°.
[IV] Correta. Se ocorre reflexão total, não há refração.
Resposta da questão 18:
[E]
6
 sen  0,91.